Table of Contents
Introduction to Cross Product of Vectors
The cross product of two vectors is a vector operation that results in a new vector orthogonal to the original vectors. It’s used to determine perpendicular, calculate torque, and find surface normals. The magnitude of the cross product signifies the area of the parallelogram formed by the input vectors..
Definition of Cross product of vectors
The cross product of two vectors A and B in three-dimensional space is a vector denoted as A × B. Its components are obtained by taking the determinants of matrices formed from the unit vectors i, j, and k and the components of A and B. The resulting vector is perpendicular to both A and B, with a magnitude corresponding to the area of the parallelogram they span. The cross product is used to compute torque, angular momentum, and surface normal.
Formula for cross product of vectors
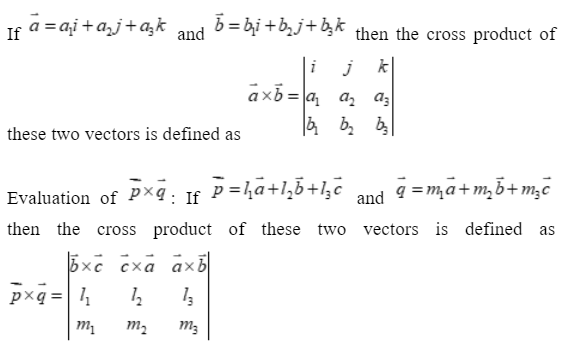
Properties of cross product of vectors
- Anticommutativity: Changing the order of vectors in the cross product changes its sign: A × B = -(B × A).
- Distributive Property: The cross product distributes over vector addition: A × (B + C) = A × B + A × C.
- Scalar Multiplication: The cross product is distributive over scalar multiplication: A × (kB) = k(A × B).
- Not Associative: The cross product is not associative: A × (B × C) ≠ (A × B) × C.
- Orthogonality: The cross product of two vectors is orthogonal to both input vectors and lies in the plane defined by them.
- Magnitude: The magnitude of the cross product corresponds to the area of the parallelogram formed by the input vectors.
- Right-Hand Rule: The direction of the cross product follows the right-hand rule: when your right-hand fingers curl from A to B, your thumb points in the direction of A × B.
Cross product of perpendicular vectors
When you take the cross product of two vectors that are perpendicular to each other, the resulting cross product vector will have a magnitude equal to the product of the magnitudes of the two input vectors, and its direction will be perpendicular to both input vectors. Mathematically, for two perpendicular vectors A and B:
|A × B| = |A| * |B|
The resulting vector will be orthogonal to both A and B, pointing in a direction that follows the right-hand rule when your right-hand fingers curl from A to B.
This property is often used to determine the area of a parallelogram spanned by the two vectors and to find the direction of the normal vector to a plane defined by these vectors.
Cross product of parallel vectors
The cross product of two parallel vectors is always zero. Mathematically, for two parallel vectors A and B:
A × B = 0
This property arises because the cross product yields a vector that’s perpendicular to both input vectors. Since parallel vectors have the same direction, there is no vector perpendicular to both of them. This property is essential for understanding the geometrical behavior of the cross product and its applications in various fields.
Magnitude of cross product of vectors
The magnitude of the cross product of two vectors A and B is given by:
|A × B| = |A| * |B| * sin(θ)
Here, |A| and |B| are the magnitudes of vectors A and B, and θ is the angle between them. This formula relates the magnitude of the cross product to the magnitudes of the input vectors and the sine of the angle between them. The magnitude of the cross product corresponds to the area of the parallelogram spanned by the two input vectors.
Also Check For:
Solved examples on cross product of vectors
Example 1: Cross Product Magnitude
Find the magnitude of cross product of vectors A = (2, 3, -1) and B = (4, -2, 5).
Solution: |A × B| = |(3 * 5 – -1 * -2), (-2 * 5 – 2 * 2), (2 * -2 – 3 * 4)|
|A × B| = |(15 – 2), (-10 – 4), (-4 – 12)|
|A × B| = |13, -14, -16|
Magnitude = √(13² + (-14)² + (-16)²) = √(169 + 196 + 256) = √621 ≈ 24.92
Example 2: Cross Product Direction
Find the direction (unit vector) of the cross product of vectors A = (1, 2, 3) and B = (-2, 0, 1).
Solution:
Calculate the cross product A × B = (2, -7, 4).
Magnitude = √(4 + (-7)² + 16) = √69.
Unit vector u = A × B / |A × B| = (2/√69, -7/√69, 4/√69).
Frequently Asked Questions on Cross Product of Vectors
What is the cross product of two vectors?
The cross product of two vectors, A and B, yields a new vector perpendicular to both input vectors. Its magnitude corresponds to the area of the parallelogram formed by the vectors, while its direction follows the right-hand rule. This operation is used in physics, engineering, and geometry for torque, area calculations, and normal vectors.
What is dot and cross product of vectors?
he dot product and cross product are two distinct vector operations: Dot Product: The dot product of vectors A and B yields a scalar quantity A · B, obtained by multiplying corresponding components and summing them. This product measures the projection of one vector onto the other and is used for work, angles, and projections. Cross Product: The cross product of vectors A and B results in a new vector A × B, calculated using component-wise multiplications and determinants. It produces a vector orthogonal to both input vectors, used for torque, normal vectors, and calculating areas. These operations have different mathematical properties and serve distinct purposes in various applications.
What is the cross product of three vectors?
he vector triple product involves three vectors: A, B, and C. It results in a new vector, often represented as A × (B × C), which is the cross product of vector B and vector C, followed by taking the cross product of vector A with the result of the first cross product. This operation has applications in physics, geometry, and vector calculus.
What is cross product used for?
The cross product of vectors has various practical applications in different fields: Physics: Used to calculate torque, angular momentum, and magnetic field strength in electromagnetism. Geometry: Determines surface normals, area of parallelograms, and planes' equations. Engineering: Applied in mechanics to analyze forces and moments, and in 3D graphics for lighting calculations. Aerospace: Used to calculate angular momentum and torque in spacecraft dynamics. Robotics: Essential for determining orientations and rotational movements in robotic systems. Crystallography: Helps analyze crystal lattice structures and molecular arrangements. Fluid Dynamics: Used to describe vortices and fluid flow in three dimensions. Computer Graphics: Applied for simulating lighting effects, shadows, and reflections in 3D scenes. Mechanical Design: Used to determine stress and strain directions in structural components. Kinematics: Helps analyze motion and velocity in complex systems.
What is the cross product of two unit vectors?
The cross product of two unit vectors will result in a vector that is perpendicular to the plane defined by the two input unit vectors. Since unit vectors have magnitudes of 1, the magnitude of the resulting cross product vector will be equal to the sine of the angle between the two unit vectors. The direction of the resulting vector will follow the right-hand rule from the first unit vector to the second unit vector.
What is the cross product of two parallel vectors?
The cross product of two parallel vectors is always zero. This is because the cross product produces a vector that is perpendicular to both input vectors. When the vectors are parallel, they have the same direction, and there is no vector that is perpendicular to both of them. Therefore, the cross product of two parallel vectors is a zero vector. Mathematically, for two parallel vectors A and B: A × B = 0.
What is the cross product of two orthogonal vectors?
The cross product of two orthogonal (perpendicular) vectors will result in a new vector that is orthogonal to both input vectors. This property aligns with the definition of the cross product, which produces a vector that is perpendicular to the plane defined by the original vectors. When the input vectors are orthogonal, the resulting cross product vector will be perpendicular to both of them.
What if the cross product of two vectors is zero?
If the cross product of any two vectors is zero, it implies that the vectors are either parallel or one of them is the zero vector (has no magnitude or direction). This is because the cross product of two parallel vectors is always zero, as well as the cross product involving a zero vector. Mathematically, for vectors A and B: A × B = 0 implies A and B are parallel or one of them is the zero vector (A or B = 0). So, the vanishing cross product indicates specific relationships between the vectors in question.








