Table of Contents
What is Identity Matrix?
An identity matrix (I or In) is a square matrix with ones on its major diagonal (from top left to bottom right) and zeros everywhere else. on other words, except for the entries on the major diagonal, all the elements in the identity matrix are zero. An identity matrix has the same number of rows as columns and is sometimes denoted by the subscript “n” (for example, I3 for a 3×3 identity matrix). When a square matrix is multiplied by its matching identity matrix, the original matrix stays intact, much like when an integer is multiplied by 1. Identity matrices are useful in linear algebra, matrix operations, and the solution of systems of equations.
Definition of an Identity Matrix
An identity matrix, abbreviated as I or In, is a square matrix with all major diagonal members being ones (1) and all other components being zeros (0). It has the feature of returning the original matrix when multiplied with any suitable matrix. In other words, the identity matrix acts in matrix multiplication like the multiplicative identity (1). An identity matrix’s size is sometimes denoted by the subscript “n” to represent a n n matrix.
Characteristics of Identity Matrix
An Identity Matrix’s primary properties are:
An identity matrix is always a square matrix, meaning it contains an equal number of rows and columns.
- Diagonal Elements: In an identity matrix, the diagonal elements are always equal to 1.
- Non-Diagonal Elements: In an identity matrix, all non-diagonal elements are always equal to 0.
- Size: An identity matrix’s size is dictated by its order, which is indicated by “n.” An n n identity matrix is made up of “n” rows and “n” columns. The outcome of multiplying an identity matrix by any compatible matrix of sufficient size is always the original matrix. To put it another way, it serves as a multiplicative identity for matrix multiplication.
- Symbol: An identity matrix is frequently designated as “I” or “In,” where the subscript “n” reflects the matrix’s order or size.
- Inverse: For square matrices, the identity matrix acts as the multiplicative identity. In terms of matrix multiplication, it may be thought of as the inverse of itself.
The identity matrix is used extensively in linear algebra, particularly in matrix operations, solving systems of linear equations, and calculating eigenvalues and eigenvectors.
The collection of input values for which the Identity Matrix is defined is referred to as the domain.
The Identity Matrix’s range is the collection of output values.
In linear transformations, multiplying a vector by an identity matrix produces the same vector while retaining its direction and magnitude.
Commutativity, associativity, and distributivity in matrix operations are some of the features of the identity matrix.
Remember that these qualities are unique to identity matrices and set them apart from other types of matrices.
Types of Identity Matrices
The Identity matrix of order
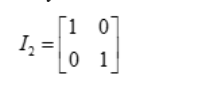
The Identity matrix of order 3
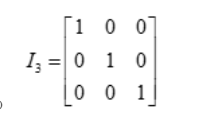
The Identity matrix of order n: It is a square matrix having n rows and n columns, in which aij = 0 for all and aij = 1 for all i = j
Also Check For Relevant Topics:
Steps to check the given Matrix is Identity Matrix or not
To determine whether a given matrix is an identity matrix, perform the following steps:
- Check if the matrix is square: An identity matrix must be square, which means that the number of rows and columns must be equal. The matrix cannot be an identity matrix if it is not square.
- Examine the diagonal elements: In an identity matrix, all diagonal elements (from top to bottom) are equal to 1. Iterate over the diagonal components until they are all 1. The matrix is not an identity matrix if any diagonal member is not equal to 1.
- Check the non-diagonal elements: All non-diagonal elements (elements outside the main diagonal) in an identity matrix should be equal to 0. Iterate over the non-diagonal elements until they are all 0. The matrix is not an identity matrix if any non-diagonal member is not equal to 0.
- If the matrix meets both requirements 2 and 3, it is said to be an identity matrix.
Examples for Identity Matrix.
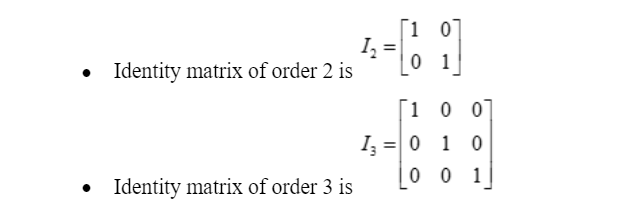
Frequently asked questions on (FAQs) Identity Matrix
Can Identity matrix be zero matrix?
No, any identity matrix is nonzero matrix, its principal diagonal elements are equal to 1 and remaining all elements are equal to zero.
Is the Identity matrix equal to 1?
The identity matrix is not at all equal to 1.
What is the shape of an Identity matrix?
The shape of identity matrix is square. The number of rows and number of columns must be equal in the Identity matrix.
What is the identity and null matrix ?
Matrix of Identity:
A square matrix with one on the main diagonal and zeros everywhere else.
For a n x n matrix, this is denoted by I or In.
In matrix multiplication, it functions similarly to the number 1 in scalar multiplication.
When multiplied by any matrix, the outcome is the same.
Multiplying with the identity matrix is the inverse of any matrix.
The Null Matrix:
All of the elements of a matrix are zero.
For a m x n matrix, this is denoted by O or O m by n.
It serves no special mathematical use in matrix multiplication.
When this matrix is multiplied by any non-zero matrix, the output is always the null matrix.
Is there any 3 x 2 Identity matrix?
No, there is no rectangular matrix as an identity matrix, because identity matrix is a square matrix.
Are Identity matrices being only square matrices
Yes, all Identity matrices are square matrices only








