Table of Contents
Introduction to Integration of log(x)
The integral of log(x) is a fundamental notion in calculus that has applications in mathematics, physics, and engineering. This article will go over the integral of log(x), its formula, proof, and important topics to remember. We will also provide solved cases and solutions to frequently asked questions.
What is integration of log(x)
The antiderivative or indefinite integral of the natural logarithm function, log(x), with regard to the variable x is found by integrating log(x). It entails finding a function whose derivative equals log(x).
The formulas for integration of log(x) and integral of ln(x)
The integration of log(x) is as below
∫log(x)dx = x (log(x) – 1) + c
Where c is constant of integration
The integration of ln(x) is as below.
∫ln(x)dx = x(ln(x) – 1) + c
Where c is constant of integration.
Proof of integration of log(x)
We utilise the integration by parts technique to verify the integral of log(x). Take a look at the integral log(x) dx.
We may rewrite the integral using integration by parts as:
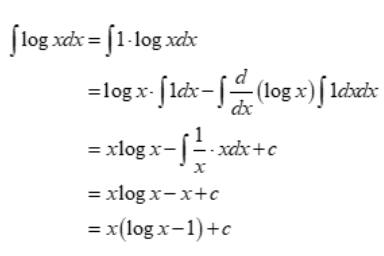
Therefore, ∫logxdx = x(logx – 1) + c
Important points on integral of log (x)
- The log(x) integration formula is used. x(log(x) – 1) + C = log(x) dx.
- When integrating the natural logarithm function, log(x), be mindful of the integration limitations and look for potential singularities.
Solved problems on integral log(x)
Find the integral of 1/x ln(x)
Solution: Take ln(x) as and then simplify the integrand
.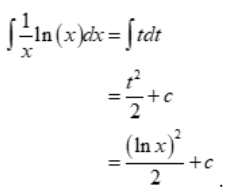
Evaluate the integral of the function ln(x) over the interval (l, e)
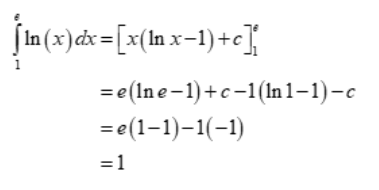
Also Check:
Frequently asked questions on Integral of log(x)
What is the integral form of ln x?
The integral form of ln x is ∫ ln x dx = x ln x - x + C, where C is the constant of integration.
What is the rule for the integral of log?
The rule for integrating the logarithmic function log(x) is: ∫ log(x) dx = x (log(x) - 1) + C, where C is the constant of integration.
What is the value of log x?
The value of log x is the logarithm of x to the base 10, commonly denoted as log₁₀ x. It represents the exponent to which 10 must be raised to get x. For example, log 100 = 2 because 10² = 100.
What is the integration of log 10 x?
The integration of log₁₀ x can be expressed as ∫ log₁₀ x dx = x (log₁₀ x - 1) + C, where C is the constant of integration.
What is the integral of e log x?
The integral of e^(log x) with respect to x is simply x + C, where C is the constant of integration. Since e^(log x) simplifies to x, its integral is straightforward.
What is the integral of log and ln?
The integrals of log and ln are different. The integral of log(x) with respect to x is x (log(x) - 1) + C, while the integral of ln(x) with respect to x is x ln(x) - x + C. Both have different forms due to their base (logarithm to base 10) and natural logarithm (logarithm to base e) properties, respectively.





