Table of Contents
Introduction to Partial Derivative
In multivariable calculus, partial derivatives are a key idea. They calculate the rate of change of a function with respect to one variable while maintaining the others constant. They are denoted by and allow us to see how a function responds to individual inputs. Partial derivatives are critical in understanding complicated systems and optimising solutions in domains such as physics and engineering.
Definition of Partial derivative
A partial derivative is a multivariable calculus term that assesses the rate of change of a function with respect to one variable while holding all other variables constant. It aids in analysing how a function responds to specific inputs and is used in many domains, including physics and engineering, to better understand complicated systems and optimise solutions..
Symbol for partial derivative
The symbol used to represent a partial derivative is ∂ (the partial derivative symbol). It is written before the function with respect to which the partial derivative is being taken and is followed by the variable with respect to which the differentiation is performed. For example, the partial derivative of a function f(x, y) with respect to x is denoted as ∂f/∂x.
Partial derivative formula
If the function f (x, y) is a two variable function in terms of x, y then the partial derivative of f with respect to x can be denoted by fx and is defined as
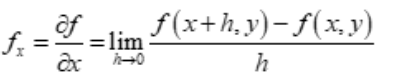
If the function f (x, y) is a two variable function in terms of x, y then the partial derivative of f with respect to y can be denoted by fx and is defined as
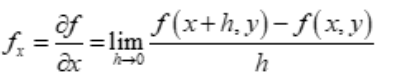
Partial differentiation with example
Partial differentiation involves finding the partial derivatives of a function with respect to one of its variables while keeping other variables constant.
Example 1
Consider the function f(x, y) = x^2 + 3xy + y^2
To find the partial derivatives of this function with respect to x and y, we perform the following differentiations:
Partial derivative with respect to x (keeping y constant):
∂f/∂x = d/dx (x^2 + 3xy + y^2) = 2x + 3y.
Partial derivative with respect to y (keeping x constant):
∂f/∂y = d/dy (x^2 + 3xy + y^2) = 3x + 2y.
Example2
Consider the function g(u, v, w) = u^3 + 2u^2v + v^2w.
To find the partial derivatives of this function with respect to u, v, and w, we perform the following differentiations:
Partial derivative with respect to u (keeping v and w constant):
∂g/∂u = d/du (u^3 + 2u^2v + v^2w) = 3u^2 + 4uv.
Partial derivative with respect to v (keeping u and w constant):
∂g/∂v = d/dv (u^3 + 2u^2v + v^2w) = 2u^2 + 2vw.
Partial derivative with respect to w (keeping u and v constant):
∂g/∂w = d/dw (u^3 + 2u^2v + v^2w) = v^2.
Rules in partial differentiation
Partial differentiation has some rules that make it easier to compute derivatives of multivariable functions. Here are the key rules for partial differentiation:
- Constant Rule: The partial derivative of a constant with respect to any variable is always zero.
For example, if c is a constant, then
∂c/∂x = ∂c/∂y = ∂c/∂z = 0. - Power Rule: To find the partial derivative of a variable raised to a constant power with respect to that variable, multiply the constant power by the variable raised to the power decreased by one.
For example : ∂/∂x (x^n) = n * x^(n-1) where n is a constant. - Sum/Difference Rule: The partial derivative of a sum or difference of two functions is the sum or difference of their individual partial derivatives.
For example: ∂/∂x (f(x, y) + g(x, y)) = ∂f/∂x + ∂g/∂x. - Product Rule:To find the partial derivative of the product of two functions with respect to a variable, use the following formula:
For example: ∂/∂x (f(x, y) * g(x, y)) = f(x, y) * ∂g/∂x + g(x, y) * ∂f/∂x. - Quotient Rule: To find the partial derivative of the quotient of two functions with respect to a variable, use the following formula:
∂/∂x (f(x, y) / g(x, y))
= (g(x, y) * ∂f/∂x – f(x, y) * ∂g/∂x) / [g(x, y)]^2. - Chain Rule: The chain rule applies to partial differentiation, just as it does in single-variable calculus. If a function is composed of two or more other functions, then the partial derivative of the composite function with respect to a variable is the derivative of the outer function evaluated at the inner function, multiplied by the partial derivative of the inner function with respect to the variable.
For example:If z = f(u, v) and u = g(x, y), then ∂z/∂x = (∂f/∂u * ∂g/∂x) + (∂f/∂v * ∂v/∂x). - Mixed Partial Derivatives:If a function has multiple variables, you can find mixed partial derivatives, which are partial derivatives taken successively with respect to different variables. The order in which you take the partial derivatives matters, and sometimes the mixed partial derivatives may not be equal (in general, they are equal if the function has continuous second partial derivatives).
For example:∂^2f/∂x∂y represents the partial derivative of f with respect to x and then y.
These rules are essential tools in calculating partial derivatives of various functions and are commonly used in applications across mathematics, physics, engineering, economics, and other fields dealing with multivariable functions.
Frequently asked questions on Partial differentiation
What is partial derivative with example?
partial derivative is a derivative of a multivariable function with respect to one of its variables, while holding all other variables constant. In other words, it measures the rate of change of the function concerning one specific variable while treating all other variables as constants. The notation used for partial derivatives involves using the symbol ∂ (the partial derivative symbol) and subscript to indicate the variable with respect to which the differentiation is performed. Let's go through an example to illustrate partial derivatives: partial derivative is a derivative of a multivariable function with respect to one of its variables, while holding all other variables constant. In other words, it measures the rate of change of the function concerning one specific variable while treating all other variables as constants. The notation used for partial derivatives involves using the symbol ∂ (the partial derivative symbol) and subscript to indicate the variable with respect to which the differentiation is performed. Let's go through an example to illustrate partial derivatives: Example: Consider the function f(x, y) = x^2 + 3xy + y^2. To find the partial derivatives of this function with respect to x and y, we perform the following differentiations: Partial derivative with respect to x (keeping y constant): ∂f/∂x = d/dx (x^2 + 3xy + y^2) = 2x + 3y. Partial derivative with respect to y (keeping x constant): ∂f/∂y = d/dy (x^2 + 3xy + y^2) = 3x + 2y.
What is partial derivative formula?
The partial derivative formula computes a multivariable function's rate of change with respect to one variable while considering the other variables as constants. It is represented by the symbol f/xi, where f is the function and xi is the variable of interest. Standard differentiation procedures are applied to the function with regard to xi in the formula.
What does ∂ means in math?
The partial derivative is represented by the symbol ∂ in mathematics. In multivariable calculus, the partial derivative determines the rate of change of a function with respect to one variable while maintaining all other variables constant. It is utilised when a function is dependent on numerous factors and allows us to see how the function varies in relation to certain variables.
What is the difference between partial derivative and ordinary derivative?
The partial derivative computes how a multivariable function changes in one variable while remaining constant in the others. It's indicated by ∂/∂x The ordinary derivative, on the other hand, computes the rate of change of a single-variable function with respect to that variable. It's represented by d/dx. The primary contrast is that partial derivatives deal with functions with several variables, whereas conventional derivatives deal with functions with a single variable.
How many types of partial derivatives are there?
Partial derivatives are classified into two types: First-order partial derivatives are a multivariable function's partial derivatives with respect to each of its variables. There are n first-order partial derivatives for a function with n variables. Higher-order partial derivatives: These are created by taking partial derivatives of a function one after the other. For example, the partial derivative of the first-order partial derivative with regard to the same variable is the second-order partial derivative. This procedure can be repeated to get third-order, fourth-order, and higher-order partial derivatives. In summary, partial derivatives are categorised depending on their order, with the two primary categories being first-order partial derivatives and higher-order partial derivatives.
Who invented partial derivative?
Over time, numerous mathematicians independently constructed partial derivatives. In the 18th and 19th centuries, Leonhard Euler, Joseph-Louis Lagrange, Augustin-Louis Cauchy, Karl Weierstrass, and Bernhard Riemann made substantial contributions to the concept's evolution, advancing calculus and mathematical analysis.
Why do we need partial differential equation?
Partial differential equations (PDEs) are crucial for characterising complicated systems with several interdependent variables. They are used to simulate phenomena like as heat transfer, fluid movement, electromagnetic fields, and quantum mechanics in physics, engineering, finance, and other areas. Solving PDEs aids in understanding and predicting real-world behaviour, allowing for technological and scientific improvements.
What are the methods of solving partial differential equations?
Depending on the kind of equation and boundary conditions, many methods are used to solve partial differential equations (PDEs). Separation of variables, method of characteristics, Fourier and Laplace transforms, finite difference methods, numerical techniques such as finite element method and finite volume method, and perturbation methods are all common approaches. Each strategy has advantages and disadvantages in certain situations.
Is d and ∂ are same?
In the context of calculus and differentiation, d and ∂ represent different types of derivatives. d (d/dx): The symbol d represents the ordinary derivative with respect to a single variable. When we write d/dx, it means the derivative of a function with respect to the variable x. ∂ (∂f/∂x): The symbol ∂ represents the partial derivative. It is used when a function depends on multiple variables. ∂f/∂x denotes the partial derivative of the function f with respect to the variable x, while holding all other variables constant. So, d and ∂ are not the same; they represent different types of derivatives: ordinary derivative and partial derivative, respectively.









