Table of Contents
Introduction to Logistic function
The logistic function, often known as the sigmoid function, is a mathematical function that is used extensively in statistics and machine learning. It converts input numbers to a range of 0 to 1, expressing probabilities or binary outcomes. It features an S-shaped curve that allows it to describe and capture nonlinear interactions seamlessly. For classification problems, the logistic function is commonly used in logistic regression and artificial neural networks..
Definition of logistic function
The logistic function, often known as the sigmoid function, is a mathematical function whose formula is:
f(x) = 1 / (1 + e^(-x))
‘e’ is Euler’s number (roughly 2.71828), and ‘x’ is the input variable. The function creates an S-shaped curve by mapping the input ‘x’ to an output range between 0 and 1. In statistics and machine learning, it is commonly used to model and predict binary events or probabilities..
Formula for logistic function
The formula for the logistic function, also known as the sigmoid function, is: f(x) = 1 / (1 + e^(-x))
where ‘e’ is Euler’s number (approximately 2.71828) and ‘x’ is the input variable. The function takes any real number as input and maps it to an output range between 0 and 1, producing an S-shaped curve. The logistic function is commonly used in statistics and machine learning for binary classification and modelling probabilities.
Derivative of logistic function
To find the differentiation of the logistic function f(x) = 1 / (1 + e^(-x)), we can use the chain rule. Let’s denote the logistic function as f(x) for simplicity.
Step 1: Rewrite the logistic function using the power rule for differentiation:
f(x) = (1 + e^(-x))^(-1)
Step 2: Apply the chain rule, which states that the derivative of a composite function is the derivative of the outer function evaluated at the inner function, multiplied by the derivative of the inner function.
f'(x) = -1 * (1 + e^(-x))^(-2) * (-e^(-x))
Step 3: Simplify the expression:
f'(x) = e^(-x) / (1 + e^(-x))^2
The derivative of the logistic function is f'(x) = e^(-x) / (1 + e^(-x))^2.
Integral of logistic function
To find the integral of the logistic function, use the formula
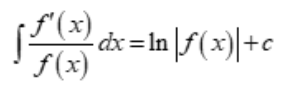
Consider the function f(x) = 1 / (1 + e^(-x)),
This can be written as f(x) = (e^(x))/(1+e^(x))
Integrate
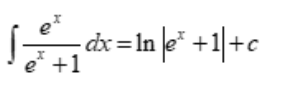
Where C is the constant of integration. The integral of the logistic function is ln|1 + e^(-x)| + C.
What is the difference between the logistic and sigmoid functions
The terms “logistic function” and “sigmoid function” are often used interchangeably, and both refer to the same mathematical function. However, in some contexts, the term “sigmoid function” is used more broadly to describe any “S-shaped” curve that maps input values to an output range between 0 and 1.
To summarize the differences between logistic and sigmoid functions:
Logistic Function: The logistic function specifically refers to the function f(x) = 1 / (1 + e^(-x)), where ‘e’ is Euler’s number and ‘x’ is the input variable. It is a type of sigmoid function and has a specific formula.
Sigmoid Function: The term “sigmoid function” can be more general and may refer to any function that produces an S-shaped curve. The logistic function is a specific example of a sigmoid function.
In practice, both terms are often used interchangeably to refer to the same function, the logistic (or sigmoid) function, which is widely used in statistics and machine learning for tasks like binary classification and modeling probabilities.
Examples for logistic function
Example 1: Logistic Regression in Binary Classification
Suppose we have a dataset with two features, ‘x1’ and ‘x2’, and a binary target variable ‘y’ (0 or 1). We want to perform binary classification to predict the probability of ‘y’ being 1 based on the features.
The logistic function (sigmoid) can be used to model the probability ‘p’ of ‘y’ being 1 given the features ‘x1’ and ‘x2’:
p = 1 / (1 + e^-(β₀ + β₁x₁ + β₂x₂))
where β₀, β₁, and β₂ are the coefficients learned during logistic regression.
Example 2: Growth Modeling in Population Biology
In population biology, the logistic function is often used to model population growth with limited resources. The logistic growth equation is given by:
P(t) = K / (1 + (K / P₀ – 1) * e^(-r * t))
where P(t) represents the population size at time ‘t’, K is the carrying capacity (maximum population size the environment can support), P₀ is the initial population size, and ‘r’ is the growth rate parameter.
The logistic function describes the growth curve of the population, starting with exponential growth and eventually leveling off as the population approaches the carrying capacity ‘K’.
These are just two examples of how the logistic function is applied in different fields to model and analyze various phenomena. Its ability to map input values to a range between 0 and 1 makes it a versatile tool in many applications.
Frequently asked questions on logistic function
What do you mean by logistic function?
A logistic function is a mathematical function that reflects the form of a S. It is used to simulate processes of development or decline that reach a saturation point over time. The logistic function is often used in statistics to predict binary outcomes or probabilities in logistic regression.
Why is it called logistic function?
The logistic function got its name because it was first used to predict logistics expansion, which has a distinctive S-shaped curve. Because of its capacity to explain processes with a limit or saturation point, it was later generalised and utilised in a variety of domains, making it valuable for forecasting probabilities and binary outcomes in statistics and other applications.
What is the basic logistic function equation?
The basic logistic function equation is f (x) = 1 / 1 + e-x Where 'e' is the base of the natural logarithm (approximately 2.71828). The function maps a real-valued input 'x' to an output between 0 and 1, exhibiting an S-shaped curve with a midpoint at x = 0. It is widely used in logistic regression and probability modelling.
What is an example of logistic function model?
A logistic function model would forecast the likelihood of a consumer making a purchase depending on their age. The logistic function may be used to simulate the link between age and the likelihood of making a purchase, with the output probability ranging from 0 (not likely) to 1 (extremely likely) as the age input varies.
What is logistic model?
A logistic model is a mathematical function, more specifically the logistic function, that is used to explain processes having S-shaped curves and a limit or saturation point. It is widely used in statistics and other domains to forecast probabilities or binary outcomes, which makes it useful in modelling various development or decline processes.
Where is the logistic function used?
The logistic function is used in various fields and applications due to its ability to model processes that have a limit or saturation point. Some common uses of the logistic function include:
Logistic Regression: In statistics, the logistic function is used in logistic regression to model binary outcomes or probabilities.
Population Growth: The logistic function is employed in biology and ecology to model population growth with limited resources.
Epidemiology: It is used to model the spread of infectious diseases and predict the number of cases over time.
Artificial Neural Networks: The logistic function is used as an activation function in certain types of artificial neural networks.
Finance: It is used in financial modelling, such as predicting probabilities of default or analysing stock price movements.
Marketing and Sales: The logistic function can model customer behaviour and predict the likelihood of purchasing products or services.
Quality Control: It is used in manufacturing to model defect rates and assess product quality.
Image Processing: The logistic function is used in image enhancement and transformation processes.
These are just a few examples of the wide-ranging applications of the logistic function in various fields due to its versatility in modelling complex processes with a saturation point.
Why is logistic function is called sigmoid
The logistic function is known as a sigmoid function because of its distinctive S-shaped curve. The name sigmoid is derived from the Greek word (sigma), which corresponds to the Greek letter S. The logistic function's curve mimics the form of the letter S, which is why it is also known as a sigmoid function. The S-shape of the curve distinguishes sigmoid functions, making them easily identifiable in a variety of mathematical and statistical applications.
Why is logistic function called regression
The logistic function is employed in a statistical procedure known as logistic regression. The term regression in logistic regression is a historical artefact that can be deceptive. The purpose of classic linear regression is to predict continuous numerical outcomes. However, the goal of logistic regression is to predict binary events or probabilities between 0 and 1. Despite its name, logistic regression is a classification algorithm, not a regression algorithm in the conventional sense. It uses the logistic function to model the relationship between the independent variables and the probability of a binary outcome, making it well-suited for binary classification tasks
Is logistic function a linear?
No, the logistic function is not a linear function. A function is considered linear if it satisfies the properties of additivity and homogeneity. In the case of the logistic function: f (x) = 1 / 1 + e-x The term e^(-x) in the denominator makes the function non-linear. The presence of exponential terms, such as e^(-x) in the logistic function, results in a curved S-shaped graph, making it non-linear.
How many types of logistic functions are there?
There are several types of logistic functions, but the two most commonly used are: Standard Logistic Function: f(x) = 1 / (1 + e^(-x)) Generalized Logistic Function (Gompertz Function): f(x) = a * e^(-b * e^(-cx)) The standard logistic function is widely used due to its simplicity and effectiveness in modeling binary outcomes and probabilities. The generalized logistic function (Gompertz function) allows for more flexibility in modeling asymmetric growth or decline processes and is commonly used in biology and epidemiology.








