Skew symmetric Matrix

Introduction to skew symmetric matrices

A skew-symmetric matrix is a form of square matrix whose transpose equals the original matrix’s negation. In other terms, n x n matrix A is skew-symmetric if A^T = -A. As a result, the matrix’s primary diagonal members are all zeros, and it has rotational or reflectional symmetry.

Definition of Skew symmetric matrix

A skew-symmetric matrix is a square matrix whose transpose equals the matrix’s negation. Mathematically, a n x n matrix A is skew-symmetric if A^T = -A. In other words, the items below the main diagonal are the inverses of the equivalent elements above the main diagonal, and the main diagonal elements are all zeros..

Examples for skew symmetric matrices:

Skew-symmetric matrices exhibit a number of intriguing characteristics. A skew-symmetric matrix’s major diagonal, for example, is made up of zeros, while the members symmetrically positioned with respect to the main diagonal have opposite signs.

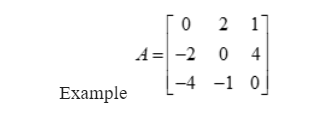
Properties of skew symmetric matrix

Here are the properties of a skew-symmetric matrix:

• A skew-symmetric matrix is always a square matrix, i.e., it has the same number of rows and columns.
• The main diagonal of a skew-symmetric matrix consists of all zeros (diagonal elements are zeros).
• The elements symmetrically located with respect to the main diagonal have opposite signs. In other words, if A[i, j] is an element, then A[j, i] = -A[i, j].
• The sum of a skew-symmetric matrix and its transpose is always a matrix with all zero elements.
• The scalar multiples of a skew-symmetric matrix also preserve its skew-symmetric property. If A is skew-symmetric and k is a scalar, then kA is also skew-symmetric.
• The determinant of a skew-symmetric matrix is zero if the matrix is of odd order. For matrices of even order, the determinant is a product of negative squares of the eigenvalues.
• Skew-symmetric matrices arise frequently in problems involving cross products and angular velocities in physics and engineering.
• The set of all skew-symmetric matrices of a given size forms a vector space.
• The product of two skew-symmetric matrices is not necessarily skew-symmetric. In general, the product of two skew-symmetric matrices is symmetric.

These properties make skew-symmetric matrices interesting and useful in various mathematical and engineering applications.

Determinant of skew symmetric matrix

Any skew-symmetric matrix of odd order has a determinant that is always zero. This feature is specific to skew-symmetric matrices and holds true for all odd-sized square matrices with members with opposing signs symmetrically opposed to the major diagonal.

he determinant of a skew-symmetric matrix of even order (an even number of rows and columns) is always a perfect square.

Eigen values of skew symmetric matrix

• A skew-symmetric matrix’s eigenvalues are always totally imaginary or zero.
• The eigenvalues of a skew-symmetric matrix A are given by = bi, where “b” is a non-zero real integer and “i” is the imaginary unit (i.e., the square root of -1).
• If the skew-symmetric matrix has an odd order, it will always have at least one eigenvalue equal to zero, and the remaining eigenvalues will be complex conjugates (i.e., bi).
• If the skew-symmetric matrix has an even order, all of the eigenvalues are purely imaginary and arrive in pairs of complex conjugates (i.e., bi).

In summary, skew-symmetric matrix eigenvalues always take the form = bi, where “b” is a non-zero real integer.

Also Check Relevant Topic:

Math Articles Math Formulas Symmetric Matrix Matrix multiplication

Frequently asked questions on skew symmetric matrix

. ” image-2=”” headline-3=”h3″ question-3=”What is skew symmetric matrix with an example? ” answer-3=”A skew-symmetric matrix is a square matrix whose negation equals its transpose. The components along the major diagonal have opposing signs. For instance, B = [0 -2 5 ; 2 0 -3 ; -5 3 0]. ” image-3=”” headline-4=”h3″ question-4=”Is skew symmetric matrix a null matrix? ” answer-4=”A skew-symmetric matrix is not always a null matrix (a matrix with all entries set to zero). Off-diagonal members of skew-symmetric matrices can have non-zero values, but the main diagonal must be zeros. A null matrix is a sort of matrix in which all of the entries are zeros, including the major diagonal. ” image-4=”” headline-5=”h3″ question-5=”What are the properties of skew symmetric matrix? ” answer-5=”Here are the properties of a skew-symmetric matrix: A skew-symmetric matrix is always a square matrix, meaning it has the same number of rows and columns. The main diagonal of a skew-symmetric matrix consists of zeros Elements symmetrically located with respect to the main diagonal have opposite signs (A[i, j] = -A[j, i]). The sum of a skew-symmetric matrix and its transpose is always a matrix with all zero elements. Scalar multiples of a skew-symmetric matrix also preserve its skew-symmetric property (k * A is also skew-symmetric). The determinant of a skew-symmetric matrix is zero for odd-sized matrices and a product of negative squares of eigenvalues for even-sized matrices. Skew-symmetric matrices are commonly used in physics and engineering applications involving cross products and angular velocities. ” image-5=”” headline-6=”h3″ question-6=”Is determinant of skew symmetric matrix is zero?” answer-6=”For an odd-order skew-symmetric matrix (an odd number of rows and columns): The determinant is always equal to zero. For an even-order skew-symmetric matrix (an even number of rows and columns): The determinant is a perfect square and equals the product of the eigenvalues’ negative squares. To summarise, the determinant of a skew-symmetric matrix of odd order is always 0, while it is a perfect square for even order. ” image-6=”” headline-7=”h3″ question-7=”What is eigen values of skew symmetric matrix? ” answer-7=”The eigenvalues of a skew-symmetric matrix are always purely imaginary or zero. For any skew-symmetric matrix A, the eigenvalues (λ) have the form λ = ± bi, where b is a non-zero real number, and i is the imaginary unit (i.e., the square root of -1). The reason for this is related to the property of skew-symmetric matrices, where the transpose of the matrix is equal to its negation. This property leads to the purely imaginary or zero nature of the eigenvalues. To find the eigenvalues of a skew-symmetric matrix, one can solve the characteristic equation det(A – λI) = 0, where A is the matrix, λ is the eigenvalue, and I is the identity matrix. The resulting eigenvalues will be purely imaginary or zero, depending on the order of the skew-symmetric matrix. ” image-7=”” count=”8″ html=”true” css_class=””]