Table of Contents
Surface tension is an interesting phenomenon exhibited by liquids.
Take a bedsheet. Stretch it horizontally in all directions. Now place a tennis ball on it. You know you can have the tennis ball get balanced on it. The ball does not tear through the bedsheet. You know gravity force of the Earth pulls the ball down. But with this experiment, you can see that elastic forces that the bedsheet applies on the ball prevent the fall of the ball through the bedsheet.

Now can you imagine that a surface layer of water also does the same, may be on a much lighter scale of mass? Yes, it is true! Most of you might have noticed a “mosquito standing on water”. The top surface layer of water is supports the entire weight of the mosquito, just as bedsheet supports the weight of the ball. Just as there is a “dent” in the bedsheet due to the weight of the ball, in the same way, there is a dent on the surface of water (though minute), below the legs of the mosquito.
We say a stretched bedsheet can support weight. In the same way, a stretched surface layer of water can also support weight. Yes, it is true that a surface layer of water is indeed stretched. If it were not stretched, then it wouldn’t have been possible for the water surface to apply tensile forces required to support the weight of a mosquito. Understand this clearly. Only stretched surfaces can apply elastic forces.
But remember, this tensile property of water is very limited. By making use of it, you can expect a mosquito’s weight being supported by water surface but you cannot expect weight of a sheep being balanced by it:-)
What is surface tension?
It is the property of a liquid by virtue of which its free surface behaves
- like a stretched membrane and
- the liquid tries to occupy minimum surface area
These properties a liquid may acquire when its surface is in contact with
- Air or gas
- Another liquid
- Solid
Why does a liquid surface try to acquire minimum surface area?
Surface of a liquid possesses peculiar properties than bulk liquid. Each liquid molecule is attracted by its neighbouring molecules. In the bulk, net force on a given molecule of the liquid is zero. But surface molecules are different. They do not practically experience forces from all sides. They experience inward attractive forces by neighbouring molecules of the same liquid in its bulk. So surface molecules are in a constant tussle to “get in”, trying to reduce surface area for the liquid. This imbalance gives rise to property of elasticity to the surface layer of liquid. The result is that under a given situation, a liquid arranges itself to have its surface area minimized.
Mathematical formula for surface tension
Imagine a flat horizontal surface of a liquid. Consider a line PQ of molecules on it. Restricting our force analysis to horizontal plane alone. Each molecule of this line of molecules is being pulled on either side of the line, by equal and opposite forces. This pull is by the neighbouring molecules. Each of these two forces acts perpendicular to the line.
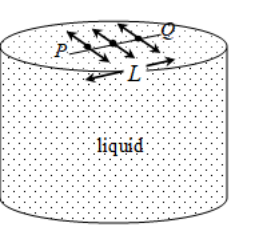
Let F be the total force on one side on this line whose length is L.
Experimentally, it is found that,
F ∝ L
F = σL, where σ is a constant of proportionality which depends on the nature of the liquid.
σ = F/L is called the surface tension of the liquid.
Important considerations while using the formula for surface tension
Consider a liquid film, like a film of soap water enclosed within a ring. It has two surfaces – front and back. Along each surface, and tangential to the surface, forces of surface tension act.
So, count the number of surfaces of liquid. Find the “appropriate length” on each surface over which the surface tension acts. That length becomes L your while using the formula F = σL.
Measuring surface tension of a liquid
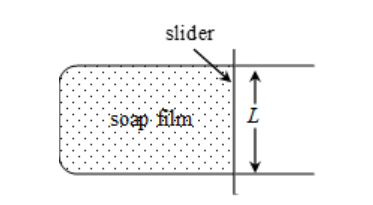
There are many ways of measuring surface tension of a liquid. One method is given below.
Imagine a soap film formed on a U-shaped smooth wire frame. A slider can slide on the two parallel arms of the frame. If the slider moves to the right, then horizontal length of the film gets increased. Since volume of liquid in the film is constant, when the horizontal length of the film increases, its thickness decreases.
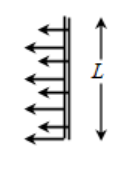
But the slider cannot move to the right on its own. In fact if left to itself, the slider moves to the left, destroying the film. Why? The slider wire is being pulled towards left by a line (comprising only of surface atoms of the liquid) that is parallel to the slider. Point to be remembered is that the film has two surfaces – front and back. So, the slider is in contact with two such parallel line of atoms, one on front surface and the other on the back surface. This is shown in the diagram. Notice carefully two sets of arrows – one set of arrows acting on the slider at the front surface and the other set of arrows acting on the slider at its back surface.
Total length of the surface molecules over which the forces of surface tension are acting is equal to 2 x L = 2L.
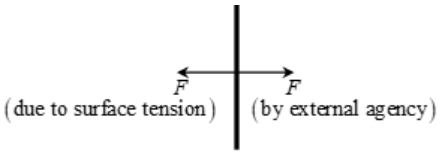
In order to make the slider not move towards left, let a force F be applied to the right. Now the slider is in equilibrium. We measure this force F.
Then surface tension of the liquid can be calculated by
σ = F/2L
Problem: –
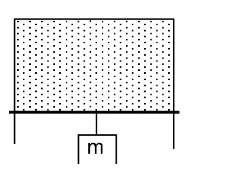
In the figure shown, a soap film is bound by a U-shaped frame on which a horizontal slider of negligible mass can slide vertically. Weight is attached to the horizontal slider so that the latter does not move.
Find the mass m (surface tension of soap solution = 0.073Nm-1, length of slider = 1m, g = 10ms-2 ).
Solution:
For equilibrium of the slider,
Downward pull due to gravity = upward pull due to forces of surface tension.
Film has two surfaces,
mg = σ x 2L
m = 2σL/g = 2 x o.o73 x 1/10 – 14.6g
Applications of surface tension
- Insects can walk on the surface of water without drowning
- A needle can be made to float on the surface of water
- Cleaning of clothes with soaps and detergents
- Small soap bubbles and rain drops are spherical
- Water rises against gravity through the tiny vessels in trees and plants
- Chemicals are sprayed on open water regions where mosquitoes are plenty. Pouring insoluble chemicals decreases surface tension of water, thereby reducing support for mosquitoes
- Water rises in a capillary tube immersed in a tub of water due to surface tension
- Suppose water is slowly forming drop (just below the tap) before it falls down from a tap. The formation of drops is due to surface tension.
- Since a liquid tries to reduce its area, a soap bubble tries to get crushed due to surface tension. But we know it does not get crushed. Why? It is because air pressure inside is greater than pressure of air outside the bubble.
Factors affecting surface tension of a liquid
Surface tension is found to be dependent on
- Temperature
- Impurities
In general, surface tension of a liquid decreases with increase in temperature. It is because cohesive force between molecules of liquid decreases when its temperature increases.
For water, presence of soluble impurities increases its surface tension. Insoluble impurities like oil decrease its surface tension.
Frequently Asked Questions on
Why are smaller drops of water spherical?
Due to surface tension, a liquid tries to occupy minimum surface area. For a given volume, a sphere has minimum surface area. Hence smaller drops of water are spherical.
Why are relatively larger drops of water not spherical, but somewhat oblate?
Apart from surface tension, force due to gravity also acts on the drop. When drops grow larger, weight starts dominating over surface tension. Hence spherical shape is deviated. For smaller drops, weight is weaker compared to surface tension. So drops are spherical.
What is the unit of surface tension?
The unit of surface tension is newton per metre.
If a soap bubble is charged, what happens to its shape and size?
Electrostatic repulsive among charges try to increase its surface area(size). If the charge is uniformly spread, then increase in size is uniform in all directions and spherical shape is retained.









