Table of Contents
What is Symmetric Matrix?
A symmetric matrix is a square matrix whose transpose is the same as its diagonal. In other words, if A is a symmetric matrix, then A = AT, where AT denotes matrix A’s transpose. The matrix is symmetric around the major diagonal, and the entries across the main diagonal stay unaltered.
Definition of Symmetric Matrix
A symmetric matrix is a square matrix in which the element in the i-th row and j-th column equals the element in the j-th row and i-th column. In other words, if A is a symmetric matrix, then for all i and j. The matrix is symmetric along its primary diagonal, with identical values reflected across the diagonal..
Key characteristics of Symmetric matrix
A symmetric matrix has the following important characteristics:
- A symmetric matrix is symmetric along its primary diagonal. This signifies that the element in the i-th row and the j-th column is the same as the element in the i-th row and the j-th column.
- A symmetric matrix is always a square matrix, which means that the number of rows equals the number of columns.
- Diagonal Entries: A symmetric matrix’s diagonal entries stay intact. The diagonal elements are represented by the element at the i-th row and i-th column.
- Transpose: A symmetric matrix’s transpose equals the original matrix. Taking the transpose has no effect on the matrix’s values or symmetry.
- Eigenvalues: Real eigenvalues exist in symmetric matrices. The eigenvectors of a symmetric matrix that correspond to different eigenvalues are orthogonal to each other.
- Positive definiteness, diagonalizability, and the spectral theorem are some of the qualities of symmetric matrices that make them valuable in linear algebra and other sciences.
- These features emphasise the distinct nature and importance of symmetric matrices in mathematical analysis and applications.
Different types of Symmetric Matrices
There are several varieties of symmetric matrices, each with its unique set of qualities and characteristics. Here are a few examples:
- A diagonal matrix is a symmetric matrix in which all non-diagonal entries are zero. Any non-zero number can be used for the diagonal elements.
- An identity matrix is a form of symmetric matrix in which all diagonal members are equal to one and all non-diagonal elements are zero. It is represented by the letter I.
- A positive definite matrix is a symmetric matrix with all of its eigenvalues being positive. It is important in optimisation issues, numerical analysis, and statistics.
- A band matrix is a symmetric matrix in which non-zero components exist within a certain bandwidth around the diagonal. The bandwidth is the number of diagonals with non-zero elements.
- Toeplitz Matrix: A Toeplitz matrix is a symmetric matrix with constant values along each diagonal from top-left to bottom-right. The components are also consistent along each anti-diagonal.
- A circulant matrix is a symmetric matrix in which each row is a cyclic shift of the row above it. It has algebraic features that are connected to Fourier analysis and signal processing.
- These are only a few instances of the many different forms of symmetric matrices.
Steps to check the given Matrix is Identity Matrix or not
To determine if a particular matrix is symmetric or not, perform the following steps:
- Check if the matrix is square: A symmetric matrix must be square, which means that the number of rows and columns must be equal. It cannot be a symmetric matrix if it is not square.
- Compare equivalent elements: Compare the i-th row and j-th column element with the j-th row and i-th column element. If the corresponding entries for all i and j are the same, the matrix is symmetric. If there are any related element pairs that are not equal, the matrix is not symmetric.
Example for Symmetric Matrix.
A symmetric matrix of order 3 is
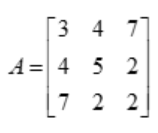
Consider the transpose of the above matrix
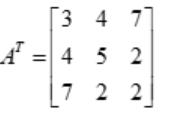
Observing the above two matrices, the matrices are are equal, Since the matrix and transpose equal, so that the above matrix is symmetric matrix.
Frequently asked questions on Identity Matrix
What is a symmetric matrix with an example?
A symmetric matrix is a square matrix that is equal to its transpose. In other words, if A is a symmetric matrix, then A = AT, where AT denotes the transpose of matrix A.
What is meant by symmetric in Matrix?
Symmetry in the context of matrices refers to a certain feature in which the matrix is equal to its transpose. A matrix A is termed symmetric if it fulfils the requirement A = AT, where AT denotes matrix A's transpose. In other words, the element in the matrix's i-th row and j-th column is equal to the element in the matrix's j-th row and i-th column. This symmetry feature suggests that the matrix has reflected symmetry along its primary diagonal. The major diagonal is made up of the entries in the matrix from top left to bottom right, and the symmetry ensures that the values above and below the main diagonal are equal.
How do you know the given matrix is symmetric
To determine if a given matrix is symmetric, perform the following steps: Examine the matrix to see if it is square (has the same number of rows and columns). Square matrices are the only ones that can be symmetric. Compare the matrix elements to their equivalent counterparts mirrored across the major diagonal (top-left to bottom-right). These members will be equivalent if the matrix is symmetric.
What is a 2 by 2 symmetric matrix
A 2 by 2 symmetric matrix is a square matrix with two rows and two columns with equal elements across the main diagonal and above and below the main diagonal.
Which matrix is called symmetric matrix?
A symmetric matrix is one that is square (has the same number of rows and columns) and has elements that are equal across the major diagonal as well as elements that are equal above and below the main diagonal.








