General Introduction to CBSE Class 11 Physics Lab Manual
Science and Physics
The word science originated from the Latin word ‘Scientia’ meaning ‘to know’. Science is a systematic attempt to understand natural phenomena in as much detail and depth as possible and use the knowledge so gained to predict, modify and control the phenomena. Science is exploring, experimenting and predicting from what we see around us. The science unravels the secrets of nature.
Physics is a basic discipline of Natural Sciences. The word Physics comes from a Greek word ‘fusis’ which means ‘nature’. Its Sanskrit equivalent is Bhautiki which means the study of physical world. Physics is the study of the basic laws of nature and their manifestation in different natural phenomena. It deals with the study oinature and natural phenomena, involving matter and energy, and their interconversion.
All quantities in terms of which laws of physics can be expressed and can be measured directly or indirectly accurately are called physical quantities.
Physical Quantities and Measurements
The process adopted for knowing the magnitude of a physical quantity, is called measurement. It is done by comparing the physical quantity with a standard of same nature. Measurement required a reference standard which is arbitrarily chosen, internationally accepted is called unit. The result of a measurement of a physical quantity is expressed by a number accompanied by a unit.
Measurement is an important part in the study of physics. Physics is an exact science.
Importance of Laboratory in Science
Science, like religion, is a search for truth. A laboratory is a place of worship, where this search is carried on. Hence to a scientist, his laboratory should be as sacred and pious as the place of worship to a devotee. In fact, laboratory is such a place of worship, where young scholars should equip themselves for something higher and nobler—a search for truth and unravelling the mystries of nature.
Aim of the Experimental study
From a careful study of history of progress of science, we conclude that an experiment is the basic foundation for the development and growth of science. The main aim of experimentation in science is to verify a given law which has already been derived from a theory. While doing an experiment with open eyes and attentive mind, new discoveries have been made during experimentation.
Physics is an experimental science. A clear understanding of its principles can be made by demonstrating the experiments by one’s own hands.
Scientific Method
A method involving systematic study of a phenomenon or systematic performance of a process, is called a scientific method.
It involves the following steps in the order given below :
(i) Aim. The phenomenon to be studied.
(ii) Apparatus. To collect the equipment (instruments) required during the study.
(iii) Experimentation. To measure the quantities involving in the phenomenon with the help of acquired instruments.
(iv) Observation. To record the numerous data (measured quantities) in a tabular form.
(v) Hypothesis. To analyse the data and find how that affects the phenomenon. Also to establish relationship between different quantities of a data, graphically or otherwise.
(vi) Verification. It is done by applying the hypothesis to other similar phenomena.
(vii) Predictions. To name new phenomena by changing the variables (quantities) involved in the study of main phenomena.
(viii) New experiments. These are done to check the existence of predictions.
(ix) Modifications. With the passage of time more refined instruments become available. Their use needs modification of old methods and procedures of experimentation. The above cycle is repeated.
Thus, experimentation is an unending process which is quite vital for the development of any kind of science. Physics is no exception.
General Instructions for an Experimental List
- Come prepared from home with the experiment you are going to perform. Read directions very closely, as in every word there is a significance without having a clear idea of what is to be done and how/why is to be done. Doubts, if any, should be got removed from the teacher before starting the experiment actually.
- Collect the necessary apparatus by request and to avoid unnecessary waste of time, the students should carefully check up each item of the working apparatus. If you do not understand the principle, construction and the use of the measuring instruments you are to use, do not hesitate to consult your teacher. It is particularly important for electrical instruments, where a slight negligence on the part of the student may damage a costly apparatus.
- Handle the apparatus very carefully, specially the small weights, nuts, screws and glass apparatus. In the event of a loss or breakage, report the matter immediately to the person concerned (Lab Incharge). Do no wait to be detected.
- Keep your table neat and clean and free from all unnecessary articles, such as hats, books, umbrellas, etc. Place them at some convenient place in the laboratory. Do not disfigure the table with chalk, pencil, ink or finger-nail marks.
- Precautions given for the experiments must be actually observed while doing the experiment.
- Do not allow water, alcohol, mercury or other chemicals to come in contact with the metallic parts of the apparatus. Apparatus so spoiled should be wiped clean with a wet cloth, dried and smeared with vaseline. Do not disfigure the wooden parts of the apparatus.
- While setting the apparatus, take care to see that the apparatus which requires frequent manipulation or reading is within easy reach. The apparatus should be arranged in an orderly manner.
- Observe twice or more the reading correctly, and write on the observation copy and get checked and signed by teacher incharge. Make correct calculation for required result and then, record it in the lab manual.
When recording an observation, do not forget to note down the units in which the measurement is made. Each quantity measured should be recorded in decimals and not in fractions. The result too should be given in proper units except when the quantity is pure ratio, e.g., specific heat, specific gravity, etc. - Always take a series of observations and as far as possible record them in a tabular form. At least one reading must be checked and verified by the teacher in charge while doing the experiments. An isolated reading is meaningless except in weighing, in taking temperatures or in measuring big lengths.
- Long and tedious calculations should be done by logarithms ; this saves time as well as reduces the chances of error.
- Do your work honestly and never cook the result by recording false observations or by making wrong calculations to show a correct result. The students should remember that the purpose of each experiment is to unmask the truth, hence nothing but truth should be recorded.
- Before leaving the laboratory
(i) The student should get his practical file signed.
(ii) All apparatuses should be returned to the laboratory assistant. No apparatus should be left on the table.
(iii) The student should get an experiment assigned for the next turn.
Recording of Experiment in the Practical File
The practical file for physics is a well-stitched notebook having left-hand page blank and right-hand page ruled. It has pages of useful formulae in the beginning and many cm graph pages at the end. A neat and systematic recording of the experiment in the practical file is very important for achieving complete success in the experimental investigations.
A student may write the experiment under the following headings in his main practical notebook. There may be slight variations in suggestions from the teacher. In that case, teacher’s instructions must be followed.
On the Left-Hand Page (Blank Page)
- Diagram. The diagram shows the sketch of the apparatus used. Different important parts must be well-labelled. Sometimes more than one diagram may be required to explain different stages of the experiment. A circuit diagram in an electricity experiment and a ray diagram for optical (light) experiment is must.
- Calculations. Formula used is written and observed values are substituted. Simplification is performed. Use log tables for multiplications and divisions and show steps of these calculations neatly in the notebook. (Do not treat log calculation as a rough work).
- Verification. The result is obtained by some other direct method and results are compared.
- Percentage error. In case the quantity determined has some standard value, percentage error is calculated by the following formula :
On the Right-Hand Page (Ruled Page)
Date……….. Experiment No…………… Page No……………………..
1. Aim. The aim of experiment to be performed should be stated clearly and precisely.
2. Apparatus. Instruments and items required for performing the experiment, are listed here.
3. Theory. In this head, the statement of the law to be verified or the principle involved in the experiment must be written. The formula used must also be written clearly explaining the symbols involved. The derivation of formula is not necessary.
4. Procedure. The different steps taken for performing the experiment must be mentioned in short. The description must be in first person and past tense (e.g., I did this. I did that).
5. Observations. First, least count of the measuring instrument must be derived and written in detail. Single observations are recorded in one or two lines. Two or more observations must be recorded in tabular form. Observations taken in single step must have three sets with changed values. For drawing a graph, six set of observations must be taken.
6. Result. Express the result with proper unit and sign.
7. Precautions taken. Mention all those precautions which were actually taken on
the instructions from the book or the teacher. Keep in mind the reasons for taking them.
8. Sources of error. These are related with the precautions to be taken. In spite of observing the precautions the apparatus may be faulty and may not give correct result. The defects in the apparatus leading to errors must be mentioned. Remember that the aim of the experiment is to learn honestly different aspects of the problem and not to arrive at a correct result by hook or crook.
Possible Errors of Observations
When a physical quantity is measured by an instrument, the result contains some uncertainty. This uncertainty is called error. Every calculated quantity which is based on the measured values, also has an error. The discrepancy between true value and measured value (observed) of a physical quantity can be termed error. The error in measurement can be classified as :
(i) Systematic error, and (ii) Random error.
(i) Systematic Error. A systematic error is one that always produces same sign (either positive or negative). This error is arised due to known factors. Systematic error can be subdivided into
(a) Instrumental error. These errors arise due to imperfection design or calibration of the measuring instrument, e.g., zero error is the instrumental error. It has a constant magnitude which can be found by measuring a known quantity from it. Suitable corrections are applied to experimental values to eliminate this error.
(b) Personal error. These arise due to an individual’s bias, lack of proper knowledge about the setting of apparatus, precautions or individual carelessness, e.g., parallex error.
Different experimental list using the same apparatus, do not obtain exactly the same result.
This error is personal error. It is because they may not be equally serious and attentive in their performances. One has to be alert to avoid it.
(c) External cause error. This error is caused when external factors such as temperature and pressure change during experiment. The changes are to be noted and correction in formula should be applied.
(d) Imperfection error. Sometimes errors arise due to imperfection in experimental
technique or procedure, e.g., the temperature measured by a thermometer of a human body will be more accurate when thermometer is placed inside the mouth rather than under the armpit.
(ii) Random Error. These errors occur irregularly without knowing the cause and hence are random with respect to sign and size. It can be called chance error, e.g., to determine the diameter of wire, a screw gauge is used. Due to non-uniform area of cross section of the wire at different places, the screw might have been tightened unevenly in the different observations. In such a case, it may not be possible to indicate which observation is most accurate. Then, an experimental list performing an experiment by taking many observations may not get identical t observations. It is a chance error. It is reduced by taking a large number of observations and then taking their mean.
Least Count and Permissible Error of a Measuring Instrument
A measuring instrument measures a quantity. The least amount of the quantity, which can be correctly measured by the measuring instrument, is called the least count (L.C.) of the instrument. All the readings or measured values are good only up to this value. This error associated with the resolution of the instrument.
The least count puts limit on the accuracy of the measuring instrument and hence some error creeps in. This error is called the permissible error of the instrument. This error occurs with both systematic and random errors. This error can be reduced by using instrument of higher precision (resolution), improving experimental technique, etc.
Accuracy of the Observations
When a quantity is measured by a measuring instrument, an error equal to half the least count is introduced in the measurement. The error will be less, if least count is less and relative error will be insignificant, if the measured quantity is very large. Therefore, the accuracy of measurement increases with the decrease in the least count of the measuring instrument.
Accuracy of Result
The result in an experiment is generally obtained by multiplying different observed quantities. The accuracy of this result depends upon the least accurate observation involved in the experiment. Hence after making calculations, the result should be expressed in such a manner that the number of decimal places in the result is the same as in the least accurate observation. The number of decimal places is reduced by rounding off the right most digit.
Hence, the result should be expressed, according to the permissible significant figures.
Rounding Off
If right most digit is less than 5, it is neglected. If it is more than 5 (say 6 to 9), it is considered as 10. It means that the digit first left to right most digit is increased by 1, then right most digit (in significant digit) is 5, then preceding digit left unchanged by if it is even and is raised by +, if it is odd. Thus rounding off has reduced decimal place by one. The same is repeated till required number of decimal places have been left.
Percentage Error
The accuracy of a result is not known by the actual amount of error, which is the difference between the actual and the experimental (or observed) value of the quantity being determined. The accuracy is known by the percentage error, which is obtained by dividing the actual error by actual value and multiplying by 100.
Significant Figures
Measurement of any physical quantity is never absolutely correct. The accuracy depends upon the least count of the measuring instrument, which becomes clear by the manner in which the result is written. If the length of an iron cylinder measured by a metre rod is 2.2 cm, it may be 2.17 cm when measured by a vernier callipers and further 2.176 cm when measured by a screw gauge. The results written have 2, 3 and 4 figures respectively. It clearly shows that measuring instruments have least count 0.1 cm, 0.01 cm and 0.001 cm, respectively. The figures (2, 3 and 4) in above example are called significant figures. In these figures, the right most figure (digit) is reasonably correct while others are absolutely correct. “The significant figures in a measured quantity indicate the number of digits in which we have confidence.” More are the significant figures in a measured value, more is the accuracy of the measured quantity and vice versa.
Rules for Finding the Significant Figures
1. All the non-zero digits are significant.
For example, 2857 contain four significant figures.
2. All the zeros between two non-zero digits are significant, no matter where the decimal point is placed,e.g., 280057, 2.80057 and 280.057 have six significant figures.
3. If the number is less than 1, the zero(s) on the right of decimal point, but to the left of the first non-zero digit are not significant. For example, 0.002857. the underlined zeros are not significant. It contains four significant figures.
4. All zeros to the right of the last non-zero digit are not significant e.g., 32800 contain only three significant digits.
5. All zeros to the right of the last non-zero digit are significant, it they come from a measurement, e.g., the distance between two stations is measured 600 km then it has three significant figures.
6. The trailing (last) zero(s) in a number with a decimal point are significant e.g., 30.00 contain four significant figures.
7. The significant figures of a measured value does not change when it is changed from one system to another system of measurement e.g., the length of a rod 234 cm = 2.34 m both have three significant figures.
Graph
Definition
A graph is a line, straight or curved, showing the relation between two variable quantities [or their powers or functions] of which one varies as a result of the change in the other. The quantity that is made to alter at will, is called the independent variable and the other which varies as a result of this change, is called the dependent variable. Thus the relation between natural numbers (independent variable) and their squares (dependent variable) can be shown by means of a graph.
Importance
A graph gives not only the relation between two variable quantities in a pictorial form, but also enables us (i) to verify certain laws such as Boyle’s Law, (ii) to find some unknown values such as the length of a second’s pendulum, (iii) to calibrate certain instruments such as an ammeter, and (iv) to find the maximum or the minimum value of a dependent variable such as angle of minimum deviation.
Plotting a Graph
Graphs are generally plotted on a paper ruled in millimetre or squares called graph paper. The following are a few simple rules that will help a student a lot in plotting a good graph:
(i) For drawing a graph, take at least six observations extending equally over a wide range.
(ii) Take a properly ruled graph paper and draw two thick lines at right angle to each other at the bottom and the left-hand edge of the paper to indicate the axes of reference. Take the horizontal line as the abscissae or X-axis and the vertical line as the ordinate or Y-axis intersecting at a point O, called the origin.
(iii) Represent the independent variable along X-axis from left to right and the dependent variable along Y-axis from below upwards. Write clearly under the X-axis and on the left of the Y-axis the quantity which is represented on each.
(iv) Examine carefully the experimental data and note the range of variation of the two variables (Physical quantities) to be plotted. Examine the number of divisions available on the two axes drawn on the graph paper. Now, choose a suitable scales for the axes keeping in mind that resulting graph should cover almost the entire portion of graph paper as shown in Fig. 1.01. This gives a suitable curve (straight line). If both the variables have zero values to begin with or you are required to find the zero position of one of the variables, take zero as the origin on both the scales. In all other cases the ’ origin need not represent zero but it should represent a round number nearest to but less than the smallest value of the corresponding variable. Mark the ends of the thick lines only to indicate the values of the variable in round numbers.
Of course, it will be more complicated to take the actual least values of the two variables at the origin.
(v) Plot the points for various pairs of corresponding values of the two variables and draw a small circle ⨀ or put a cross (x) round each of the plotted points.
(vi) If the plotted points appear to be nearly in a straight line, draw a straight line, passing exactly through most of the points and symmetrically through the rest. If the points do not appear to be in a straight line, draw a free hand smooth curve so that the maximum number of points lie exactly on it and the rest are evenly distributed on either side of it.
(vii) Write the name of the graph at the top of the graph paper in words “graph showing the relation between [independent variable] andy [dependent variable].”
(viii) Write down the proper scales taken along both the axes, under the graph heading.
(ix) Use a millimeter graph for greater acccuracy in the result.
Some Well-Known Geometrical Figures Obtained by Graph
Logarithms
Logarithm literally means a rule to shorten Arithmetic, reduces to a few days the labour of many months, and doubles, as it were, the life of a mathematician besides freeing him from the errors and disgust inseparable from long calculations. —Laplace
Logarithms were invented by Napier.
My lord, I have undertaken this journey purposely to see your person, to know by what engine of wit or ingenuity you came first to think of this most excellent help in Mathematics, viz., the logarithms. —Briggs to Napier
Definition and Notation. If ax =N,x is called the logarithm of N to the base a, and is denoted by loga N [read as log N to the base a].
[In words. The logarithm of a number to a given base is the index of the power to which the base must be raised to equal that number.]
Example, v 23 = 8 .*. 3 is the logarithm of 8 to the base 2 i.e., log28 = 3.
Logarithms are of two types :
(i) Naperian, in which the base is e. They are not used in practice.
(ii) Common, in which the base is 10. They are commonly used. When the base is not mentioned, it is implied that the base is 10. Tables of logarithms of natural numbers to the base 10 are given at the end of the book.
Common Logarithm
Logarithm of a number consists of two parts :
(i) Characteristics is the integral part [whole or natural number].
(ii) Mantissa is the fractional part generally expressed in decimal form.
Note. The mantissa is always positive.
How to find the Characteristic of a number ?’The characteristic depends on the magnitude of the number and is determined by the position of the decimal point. For number greater than one, the characteristic is positive and one less than the number of digits to the left of the decimal point. For numbers smaller than one [decimal fractions], it is negative and one more than the number of zeros between the decimal point and first digit.
How to find the Mantissa of a number ? The value of mantissa depends on the digits and their order and is independent of the position of the decimal point. As long as the digits and their order is the same the mantissa is the same, whatever be the position of the decimal point.
The logarithm tables give the mantissa only. They are usually meant for numbers con-taining four digits, and if a number consists of more than four figures, it is rounded-off to four figures after determining the characteristic. To find mantissae, the tables are consulted in the following manner :
(i) The first two significant figures of the number are found at the extreme left vertical column of the table wherein the number lying between 10 and 99 are given. The mantissae of the figures which are less than 10 can be determined by multiplying the figures by 10.
(ii) Along the horizontal line in the topmost column the figures
are given. These correspond to the third figure of the given number.
Example 1. Find the logarithm of368.6.
The number has 3 figures to the left of the decimal point. Hence its characteristic is 2.
To find the mantissa, ignore the decimal point and look for 36 in the first vertical column and 8 in the central topmost column. Proceed from 36 along a horizontal line towards the right and from 8 vertically downwards. The two lines meet at a point where the number 5658 is written. This is the mantissa of 368. Proceed further along the horizontal line and look verti¬cally below the figure 6 in difference column. You will find the figure 7 there. Hence the mantissa of 3686 is 5658 + 7 = 0.5665.
.-. The logarithm 368.6 is 2.5665 (log 368.6 = 2.5665),
Example 2. Find the logarithm of368600.
The characteristic of this number is 5 and the mantissa is the same as in example 1.
.-. log 368600 = 5.5665.
Example 3. Find the logarithm of 0.00368633.
The characteristic of this number is 3 as there are two zeros following the decimal point. We can find the mantissa of only 4 significant figures. Hence we neglect the last 2 figures (33) and find the mantissa of 3686 which is 5665.
.-. log 0.00368633 = 3.5665.
When the last figure of a number consisting of more than 4 significant figures is equal to or more than 5, the figure next to the left of it is raised by one and so on till we have only 4 significant figures and if the last figure is less than 5 it is neglected as in the last example.
If we have the number 3686.58, the last figure is 8, therefore, we shall raise the next figure to 6 and since 6 is again more than 5 we shall raise the next figure to 7 and find the logarithm of 3687.
Antilogarithm. The number whose logarithm is x is called the antilogarithm of x and is denoted by antilog x.
Thus, since log 2 = 0.30103, antilog 0.30103 = 2.
Example 1. Find the number whose logarithm is 1.6078.
(i) Removing 1 (the integral part) from the given logarithm, we get 0.6078. The first two figures from the left are 0.60, the third figure is 7 and the fourth is 8.
(ii) In the table of the antilogarithms, look in the first vertical column for .60. In this horizontal row under the column headed by 7, we find the number 4046 at the intersection.
(iii) In the continuation of this horizontal row and under the mean differences column on the right headed by 8, we find the number 7 at the intersection. Adding 7 to 4046, we get 4053. Now 4053 is the figure of which 0.6078 is the mantissa.
(iv) The characteristic = 1. This is one less than the number of digits in the integral part of the required number, hence the number of digits in the integral part of the required number = 1 + 1 = 2. The required number is 40.53 i.e., antilog 1.6078 = 40.53.
Example 2. Find the antilogarithm of 2.6078.
As the characteristic is 2, there should be one zero on the right of decimal in the number. Hence antilog 2.6078 = 0.04053.
Laws of Logarithms. From the laws of indices, we obtain the following laws of logarithms :

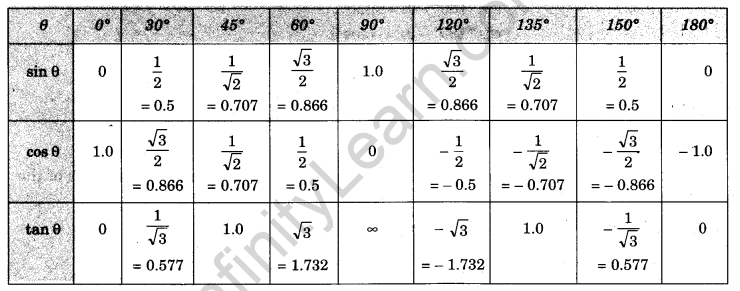
Trigonometric Ratios
Let ABC be a right-angled triangle having a right angle at C (Fig. 1.03). Let the angle at A be denoted by 0. In this triangle, AB is the hypotenuse. AC is the base and BC is the perpendicular.

Ratios of Angles between 90° and 180°
The following simple formulae can be utilised to find the trigonometrical ratios of angles between 90° and 180°
T-Rations of Angles between 180° and 360°
The following simple formulae can be utilized to find the trigonometrical ratios of the angles between 180° and 360°
Trigonometrical Formulae

T-Rations of Some Common Angles