Table of Contents
Introduction:
Surface area refers to the total area that covers the outer surface of a three-dimensional object. It represents the sum of all the individual areas of the object’s faces, including the bases, sides, and curved surfaces. The surface area is a fundamental concept used to measure and analyze the extent of coverage of an object in terms of square units.
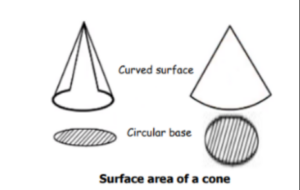
What is the Surface area of a cone?
- The surface area of the cone is the sum of the area of the circular base and the area of the curved surface.
- The curved surface when opened is the sector of a circle.
What is a right circular cone?
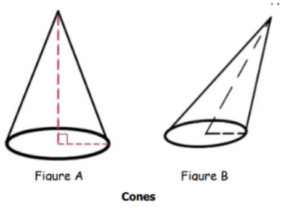
A cone in which its axis is perpendicular to the circular base is called a Right circular
cone.
- In the below figure, cone A is a right circular cone, but cone B is not.
- When a right triangle is moved around its axis, it forms a circular base and a slant
curved surface. The resulting figure is a cone.
- The top of the cone is the vertex.
- The line passing through the vertex and the centre of the circular base is the axis.
The axis of this cone is perpendicular to its base and hence it is known as a right
circular cone.
What is the Surface area of a right circular cone?
The Surface area of a right circular cone is equal to the sum of the areas of the circular base of the cone and its curved surface.
Derivation:
Consider the right circular cone as shown below.
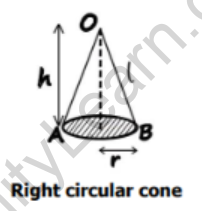
Point O is the vertex of the cone. Points A and B are marked on the circumference such that AB forms a diameter.
Let l be the slant height, h be the perpendicular height, and r be the radius of the circular base.
Surface area of right circular cone = Area of curved surface + Area of circular base … (i)
Area of circular base =πr2 …(ii)
Area of curved surface = Area of sector AOB

For the above sector OAB, the radius is OA = OB = slant height of cone = l
Area of sector OAB =

Now, length of arc AB =

In the case of the cone,
Length of arc AB = circumference of circular base = 2πr …..(v)
From statements (iv) and (v),
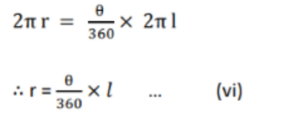
Area of sector OAB =

From statements (vi) and (vii),
Area of sector OAB = πlr
∴ Area of curved surface = πlr ….(viii)
From statements (i), (ii), and (viii),
Surface area of right circular cone = πlr + πr2
∴ Surface area of right circular cone =πr(l+r)
Solved Examples on Surface Area of a Cone:
Example 1: Find the surface area of a cone with a radius of 5 cm and a slant height of 8 cm.
Solution:
Using the formula SA = πr(r + l),
SA = π × 5(5 + 8)
= π × 5 × 13
≈ 201.06 cm²
The surface area of the cone is approximately 201.06 cm².
Example 2: A cone has a radius of 3.5 cm and a height of 10 cm. Calculate its surface area.
Solution:
To find the slant height, we can use the Pythagorean theorem:
l = √(r² + h²) = √(3.5² + 10²) ≈ 10.84 cm
Using the formula SA = πr(r + l),
SA = π × 3.5(3.5 + 10.84)
≈ 147.28 cm²
The surface area of the cone is approximately 147.28 cm².
Conclusion:
The surface area of a cone is the sum of the area of its circular base and the area of its curved lateral surface. The formula to calculate the surface area of a cone is given by SA = πr(r + l), where r is the radius of the base and l is the slant height of the cone. It is an important measurement when determining the amount of material needed to cover or paint a cone-shaped object.
Frequently Asked Questions on Surface Area of a Cone Formula
What is the surface area of the cone?
The surface area of a cone is the sum of the area of its circular base and the area of its curved lateral surface. The formula to calculate the surface area of a cone is SA = πr(r + l), where r is the radius of the base and l is the slant height of the cone.
How many types of cones are there?
A cone can be classified into two main types: the Right Circular Cone and the Oblique Cone. The Right Circular Cone has a circular base with an axis that passes through the center of the base. The vertex is positioned directly above the center, forming a right angle with the base. On the other hand, the Oblique Cone also has a circular base, but its axis is not perpendicular to the base, resulting in a slanted or tilted appearance.
What is the surface area of a 3D shape?
The surface area of a 3D shape refers to the total area of all its outer surfaces. It is calculated by summing up the areas of each individual face or surface of the shape. The surface area is measured in square units, such as square centimeters or square meters, depending on the units used for the measurement of the shape.
How do I find the surface area and volume of a cone?
To find the surface area of a cone, use the formula SA = πr(r + l), where r is the radius and l is the slant height. For the volume, use the formula V = (1/3)πr²h, where r is the radius and h is the height.
What is the flat surface area of a cone?
The flat surface area of a cone, also known as the lateral surface area, refers to the combined area of all the curved sides of the cone, excluding the base. It can be calculated using the formula A = πrl, where r is the radius of the base and l is the slant height of the cone.
How many surface areas does a cone have?
A cone has two surface areas: the curved surface area and the base area. The curved surface area refers to the area of the lateral surface, which is the curved part of the cone excluding the base. The base area is the area of the circular base of the cone. Therefore, a cone has a total of two surface areas.
What does surface area depend on?
The surface area of an object depends on its shape and size. For different geometric shapes, such as cubes, spheres, cylinders, or cones, the formulas to calculate surface area are specific to each shape. The surface area also depends on the dimensions of the object, such as the length of its sides, the radius of its base, or the height of its sides.
How to calculate the slant height of a cone?
To calculate the slant height of a cone, you can use the Pythagorean theorem. The slant height (l) can be found by applying the theorem to the triangle formed by the radius (r), height (h), and slant height (l). The formula is: l = √(r² + h²) Here, r is the radius of the base of the cone, and h is the height from the apex to the base. By substituting the known values into the formula, you can find the slant height of the cone.









