Surface Area Formulas

Introduction

The surface area of a three-dimensional object is the total area of all its faces. In real-life we use the concept of surface areas of different objects when we want to wrap something, paint something, and eventually while building things to get the best possible design. Let us learn all about the surface area of 3D shapes in this article.

The total area occupied by the surfaces of an object is called its surface area. In geometry, different 3D shapes have different surface areas which can be easily calculated using the formulas that we will be learning in this article. The surface area is classified into two categories:

Lateral surface area or Curved surface area

Total surface area

Surface Area Formulas

Surface area is the measure of the total area of the external surfaces of a three-dimensional object. It is an important concept in geometry and is used to quantify the amount of material needed to cover or coat an object. Here are some key points and formulas related to surface area:

1. Cuboid:

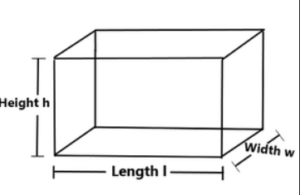
The surface area of a rectangular prism is given by the formula:

Surface Area = 2(length × width + width × height + height × length)

 

2. Cube:

 

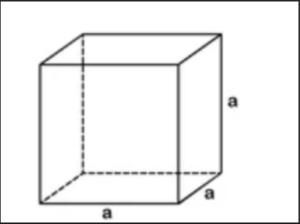
The surface area of a cube is given by the formula:
Surface Area = 6(side length)2

 

3. Cylinder:

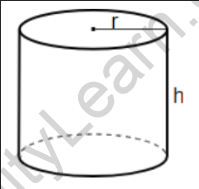
The surface area of a cylinder is the sum of the areas of its two circular bases and the lateral surface area.
The formulas are: Surface Area = 2πr2+ 2π(radius)(height)

4. Sphere:

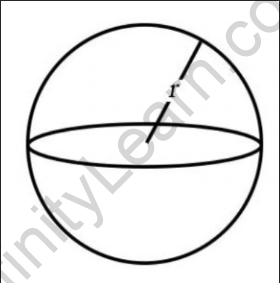
The surface area of a sphere is given by the formula:
Surface Area = 4π(radius2)

5. Cone:

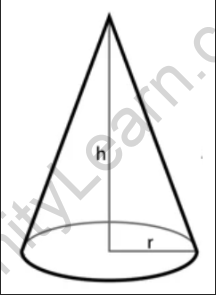
The surface area of a cone is the sum of the area of its base and the lateral surface area. The formulas are: Surface Area = π(radius2) + π(radius)(slant height)

 

6. Pyramid:

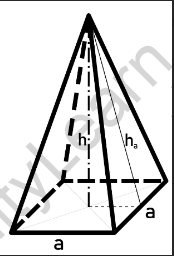
The surface area of a pyramid is the sum of the area of its base and the areas of its lateral faces. The formulas depend on the shape of the base.

These formulas provide a way to calculate the surface area of various geometric shapes. Understanding surface area allows us to determine quantities such as the amount of paint needed to cover an object, or the material required to construct it. It is an essential concept in many fields, including architecture, engineering, and manufacturing.

Solved Examples on Surface Formulas:

Example 1: Surface Area of a Cuboid
Given:

Length = 5 cm

Width = 3 cm

Height = 4 cm

To find the surface area:

Surface Area = 2(length × width + width × height + height × length)

Surface Area = 2(5 × 3 + 3 × 4 + 4 × 5)

Surface Area = 2(15 + 12 + 20)

Surface Area = 2(47)

Surface Area = 94 square cm

Therefore, the surface area of the rectangular prism is 94 square cm.

Example 2: Find the surface area of the Cylinder given below.

Given:

Radius = 2 cm

Height = 6 cm

To find the surface area:

Surface Area = 2π(radius2) + 2π(radius)(height)

Surface Area = 2π(22) + 2π(2)(6)

Surface Area = 2π(4) + 2π(12)

Surface Area = 8π + 24π

Surface Area = 32π square cm

Therefore, the surface area of the cylinder is 32π square cm, or approximately 100.53 square cm.

Example 3: Surface Area of a Sphere

Given:

Radius = 3 cm

To find the surface area:

Surface Area = 4π(radius2)

Surface Area = 4π(32)

Surface Area = 4π(9)

Surface Area = 36π square cm

Therefore, the surface area of the sphere is 36π square cm, or approximately 113.1 square cm.

Frequently Asked Questions on Surface Formula:

1: What is the TSA of a cylinder?

Answer: The total surface area (TSA) of a cylinder is the sum of the areas of its two circular bases and its curved surface. The formula to calculate the TSA of a cylinder is:

TSA = 2πr(r + h)

Where:

TSA represents the total surface area of the cylinder,

π is the mathematical constant pi (approximately 3.14159),

r is the radius of the circular base of the cylinder, and

h is the height of the cylinder.

By substituting the values of the radius and height into the formula, you can calculate the TSA of the cylinder. Remember to use consistent units for the measurements to obtain the correct result.

2: What is CSA in maths?

Answer: In mathematics, CSA stands for Curved Surface Area. It refers to the total area of the curved surface of a three-dimensional object, excluding any flat or base surfaces. The CSA is specifically used to calculate the surface area of objects with curved surfaces, such as cylinders, cones, and spheres. It is an important concept in geometry and is used in various calculations and formulas related to surface area and volume of curved objects.

3: Does changing the size or shape of an object affect its surface area?

Answer: Yes, changing the size or shape of an object can affect its surface area. For example, increasing the dimensions of a rectangular prism will increase its surface area, while changing the shape of an object may require different formulas to calculate its surface area.

4: How do you calculate the surface area of a three-dimensional object?

Answer: The formula for calculating surface area depends on the shape of the object. For example, the surface area of a cube is found by multiplying the length of one side by six, while the surface area of a cylinder involves calculating the areas of its bases and its curved surface.

5: What is surface area?

Answer: Surface area is the measure of the total area of the external surfaces of a three-dimensional object. It represents the amount of material needed to cover or coat the object.

6: Is Surface Area the Same as Area?

Answer: The main difference between surface area and area is that surface area is the area of 3D shapes such as a sphere, cylinder, and so on, whereas, area is the measurement of the space occupied by 2D shapes such as triangles, squares, and so on.

7: How to Find the Surface Area of a Rectangular Prism?

Answer: The surface area of a rectangular prism can be calculated by using the following formula: Surface area of rectangular prism = 2(lw + wh + lh), where l, w, and h are the length, width, and height of the rectangular prism respectively.

8: What is the Surface Area of a Cube?

Answer: A cube is made up of 6 square faces. So, the surface area of a cube is the sum of the areas of all those 6 faces. We know that area of a square = a2, where a is the side length of the square. So, the surface area of a cube with side length a is 6a2.