To Find the Weight of a Given Body Using Parallelogram Law of Vectors

To Find the Weight of a Given Body Using Parallelogram Law of Vectors

Aim
To find the weight of a given body using parallelogram law of vectors.

Apparatus
Parallelogram law of forces apparatus (Gravesand’s apparatus), plumb line, two hangers with slotted weights, a body (a wooden block) whose weight is to be determined, thin strong or thread, white drawing paper sheet, drawing pins, mirror strip, sharp pencil, half metre scale, set squares, protractor.

Theory

Diagram

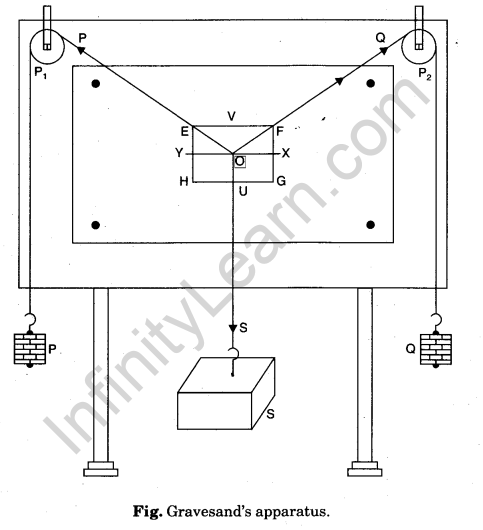
Procedure

1. Set up the Gravesand’s apparatus with its board vertical, tested with the help of a plumb line.
2. Test that pulleys P₁ and P₂ are frictionless. Oil them if necessary.
3. Fix the white drawing paper sheets on the board with the help of drawing pins.
4. Take three pieces of strong thread and tie their one end together to make knot O. This knot becomes junction of the three threads.
5. From the other ends of two threads, tie a hanger with some slotted weights in each. These serve as the weights P and Q. From the other end of third thread tie the given body S.
6. Pass threads with weights P and Q over the pulleys and let the third thread with given body S, stay vertical in the middle of the board.
7. Adjust the weights P and Q (forces) such that the junction O stays in equilibrium slightly below the middle of the paper.
8. The weights P, Q and wooden block S act as three forces
   
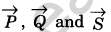
   acting along the three threads at the junction O. The forces are in equilibrium.
9. See that all the weights hang freely and none of them touches the board or the table.
10. Mark the position of junction O on the white paper sheet by a sharp pencil.
11. Disturb weights P and Q and leave them.
12. Note position of junction O. It must be very close to earlier position. (If not, oil the pulleys to remove friction.)
13. Keeping mirror strip lengthwise under each thread, mark the position of the ends of the image of thread in the mirror, covering the image by the thread (this removes parallax error). The position are P₁ ,P₂ for thread of weight P, Q₁ and Q₂ for thread of weight Q and S₁ , S₂ for thread of weight S as shown in figure.
    
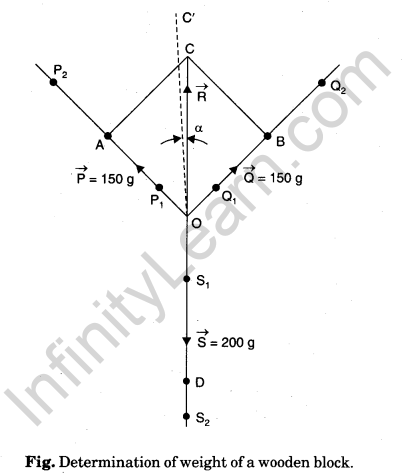
14. Remove paper from the board.
15. With the help of a half metre scale draw lines through points P₁ and P₂ to represent P, through points Q₁ and Q₂ to represent Q and through points S₁ and S₂ to represent S. These lines must meet at point O.
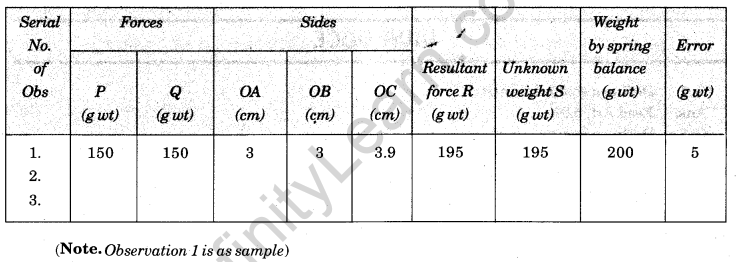
16. Taking a scale, 1 cm = 50 g, take OA = 3 cm and OB = 3 cm to represent P = 150 g and Q = 150 g.
17. Complete parallelogram OACB using set squares and join OC. It represents R.
18. Measure OC. It comes to be 3.9 cm.
19. For different sets of observation, change P and Q suitably.
20. Find weight of the wooden block by a spring balance.

Observation
Least count of spring balance =………. g
Zero error of spring balance =………..g
Weight of unknown body by spring balance = ………..g
Scale. Let 1 cm = 50 g.

Calculations

Result
The unknown weight of given body = 195 g
The error is within limits of experiment error.

Precautions

1. The board should be stable and vertical.
2. The pulleys should be friction less.
3. The hangers should not touch the board or table.
4. Junction O should be in the middle of the paper sheet.
5. Points should be marked only when weights are at rest.
6. Points should be marked with sharp pencil.
7. Arrows should be marked to show direction of forces.
8. A proper scale should be taken to make fairly big parallelogram.

Sources of error

1. Pulleys may have friction.
2. Weights may not be accurate.
3. Points may not be marked correctly.
4. Weight measured by spring balance may not be much accurate.

Viva Voce

Question. 1. Define a scalar quantity.
Answer. Read Art. 5.01.

Question. 2. Define a vector quantity.
Answer. Read Art. 5.01.

Question. 3. How a geometrical vector represents a vector quantity ?
Answer. Read Art. 5.02.

Question. 4. Define addition of vectors.
Answer. Read Art. 5.03.

Question. 5. State parallelogram law of addition of two vectors.
Answer. Read Art. 5.04 (a).

Question. 6. Write expression for magnitude and direction of the resultant of two vectors.
Answer. The required expression are

Question. 7. State triangle law of addition of two vectors.
Answer. Read Art. 5.05 (a).

Question. 8. Define equilibrium of vectors.
Answer. Read Art. 5.06.

Question. 9. Define an equilibrant vector.
Answer. Read Art. 5.06.

Question. 10. State triangle law for equilibrium of three vectors.
Answer. Read Art. 5.07 (a).

Question. 11. Can the law of vectors be used to add forces and velocities ?
Answer. Yes, they can be used, because forces and velocities are also vectors.

Question. 12. Why is addition of vectors different from addition of scalars ?
Answer. Because vectors have direction also, which makes all the difference.

Question. 13. Why is addition of vectors called composition of vectors ?
Answer. Composition means collection. By addition we collect (convert) many vectors into one single vector.

Question. 14. What is meant by resolution of vectors ?
Answer. It is reverse of composition of vectors. The breaking of a single vector into its components is called resolution of vectors.

Question. 15. What are rectangular components ?
Answer. The two components of a vector, which are perpendicular to each other, are called rectangular (or right angular) components.

Question. 16. What are the main sources of error in the experiment using Gravesand’s apparatus ?
Answer. Its sources of error are
(1) Friction in the pulleys.
(2) Weights in the threads.

Question. 17. Why the thread junction does not come at rest at same position always ?
Answer. It is due to friction on the pulleys.

Question. 18. How can this friction be reduced ?
Answer. It is done by oiling the pulleys.

Question. 19. Why the suspended weights are kept free from board or table ?
Answer. So that their effective weight may not become different due to reaction of board or table.