NCERT Exemplar Solutions for Class 9 Maths Chapter 5 – Introduction to Euclid’s Geometry

Introduction to Euclid’s Geometry is a crucial chapter for students preparing for Class 9 Maths. It introduces the foundational concepts of geometry through the work of the ancient Greek mathematician Euclid, which is essential for building a strong base in understanding geometric theorems and axioms.

This chapter covers:

• Basic Definitions of Geometry: Learn about points, lines, and planes, and how these basic elements form the foundation of all geometric studies.
• Euclid’s Axioms and Postulates: Understand Euclid’s approach to geometry, which consists of assumptions (axioms) and logical deductions (postulates) that help form geometric theorems.

By going through the NCERT Exemplar Solutions provided here, students can gain a better understanding of the basic structure and logic of geometry, which will be beneficial not only for their exams but also for further studies in Mathematics.

Download the PDF of NCERT Exemplar Solutions for Class 9 Maths Chapter 5 Introduction to Euclid’s Geometry

Download detailed step-by-step solutions PDF for all the exercises in NCERT Class 9 Maths Chapter 5: Introduction to Euclid’s Geometry. These solutions are designed to help students understand the concepts clearly and solve problems with confidence.

Key Concepts Covered:

• Definition of Point and Line: Explanation of the most fundamental terms in geometry.
• Euclid’s Five Postulates: Understanding the basis of Euclid’s geometry, from the first postulate (a straight line may be drawn from any point to any other point) to the fifth postulate (the famous parallel postulate).
• Proofs and Theorems: Logical deductions from the postulates are used to prove basic theorems in geometry.

By practicing these exemplar problems, students will be able to master the logic and reasoning skills required to excel in geometry.

Access Answers to NCERT Exemplar Solutions for Class 9 Maths Chapter 5 Introduction to Euclid’s Geometry

Question 1. The three steps from solids to points are:

(A) Solids-surfaces-lines-points

(B) Solids-lines-surfaces-points

(C) Lines-points-sufaces-solids

(D) Lines-surfaces-points-solids

Solution: (A): The three steps from solids to points are solids-surfaces-lines-points.

Question 2. The number of dimensions, a solid has:

(A) 1

(B) 2

(C) 3

(D) 0

Solution: (C): A solid e.g., Cuboid has shape, size, and position. So, solid has three dimensions.

Question 3. The number of dimensions, a surface has:

(A) 1

(B) 2

(C) 3

(D) 0

Solution: (B): Boundaries of a solid are called surfaces. A surface (plane) has only length and breadth. So, it has two dimensions.

Question 4. The number of dimension, a point has

(A) 0

(B) 1

(C) 2

(D) 3

Solution: (A): A point is that which has no part i. e., no length, no breadth and no height. So, it has no dimension.

Question 5. Euclid divided his famous treatise “The Elements” into

(A) 13 chapters

(B) 12 chapters

(C) 11 chapters

(D) 9 chapters

Solution: (A)

Euclid divided his famous treatise ‘The Elements” into 13 chapters.

Question 6. The total number of propositions in the Elements are

(A) 465

(B) 460

(C) 13

(D) 55

Solution: (A)

The statements that can be proved are called propositions or theorems. Euclid deduced 465 propositions in a logical chain using his axioms, postulates, definitions and theorems.

Question 7. Boundaries of solids are:

(A) surfaces

(B) curves

(C) lines

(D) points

Solution: (A): Boundaries of solids are surfaces.

Question 8. Boundaries of surfaces are:

(A) surfaces

(B) curves

(C) lines

(D) points

Solution: (B) : The boundaries of surfaces are curves.

More Resources for Class 9

• NCERT Exemplar for Class 9
• NCERT Exemplar for Class 9 Science

Question 9. In Indus Valley Civilization (about 3000 B.C.), the bricks used for construction work were having dimensions in the ratio

(A) 1 : 3 : 4

(B) 4 : 2 : 1

(C) 4 : 4 : 1

(D) 4 : 3 : 2

Solution: (B)

In Indus Valley Civilization, the bricks used for construction work were having dimensions in the ratio length : breadth : thickness = 4 : 2 : 1.

Question 10. A pyramid is a solid figure, the base of which is

(A) only a triangle

(B) only a square

(C) only a rectangle

(D) any polygon

Solution: (D)

A pyramid is a solid figure, the base of which is a triangle or square or some other polygon.

Question 11. The side faces of a pyramid are

(A) Triangles

(B) Squares

(C) Polygons

(D) Trapeziums

Solution: (A)

The side faces of a pyramid are always triangles.

Question 12. It is known that, if x + y = 10, then x + y + z = 10 + z. The Euclid’s axiom that illustrates this statement is:

(A) First Axiom

(B) Second Axiom

(C) Third Axiom

(D) Fourth Axiom

Solution: (B)

The Euclid’s axiom that illustrates the given statement is second axiom. According to this, if equals are added to equals, the wholes are equal.

Question 13. In ancient India, the shapes of altars used for household rituals were:

(A) Squares and circles

(B) Triangles and rectangles

(C) Trapeziums and pyramids

(D) Rectangles and squares

Solution: (A)

In ancient India, squares and circular altars were used for household rituals.

Question 14. The number of interwoven isosceles triangles in Sriyantra (in the Atharvaveda) is:

(A) Seven

(B) Eight

(C) Nine

(D) Eleven

Solution: (C)

The Sriyantra (in the Atharvaveda) consists of nine interwoven isosceles triangles.

Question 15. Greek’s emphasised on:

(A) Inductive reasoning

(B) Deductive reasoning

(C) Both (A) and (B)

(D) Practical use of geometry

Solution: (B)

Greek’s emphasised on deductive reasoning.

Question 16. In ancient India, altars with combination of shapes like rectangles, triangles and trapeziums were used for

(A) Public worship

(B) Household rituals

(C) Both (A) and (B)

(D) None of A, B, C

Solution: (A)

In ancient India altars whose shapes were combinations of rectangles, triangles and trapeziums were used for public worship.

Question 17. Euclid belongs to the country:

(A) Babylonia

(B) Egypt

(C) Greece

(D) India

Solution: (C)

Euclid belongs to the country Greece.

Question 18. Thales belongs to the country:

(A) Babylonia

(B) Egypt

(C) Greece

(D) Rome

Solution: (C)

Thales belongs to the country Greece.

Question 19. Pythagoras was a student of:

(A) Thales

(B) Euclid

(C) Both (A) and (B)

(D) Archimedes

Solution: (A)

Pythagoras was a student of Thales.

Question 20. Which of the following needs a proof ?

(A) Theorem

(B) Axiom

(C) Definition

(D) Postulate

Solution: (A)

The statements that needs a proof are called propositions or theorems.

Question 21. Euclid stated that all right angles are equal to each other in the form of

(A) an axiom

(B) a definition

(C) a postulate

(D) a proof

Solution: (C)

Euclid stated that all right angles are equal to each other in the form of a postulate.

Question 22. ‘Lines are parallel, if they do not intersect’ is stated in the form of

(A) an axiom

(B) a definition

(C) a postulate

(D) a proof

Solution: (B)

‘Lines are parallel, if they do not intersect’ is the definition of parallel lines.

NCERT Exemplar Class 9 Maths Chapter 5 Exercise 5.2

Question 1. Euclidean geometry is valid only for curved surfaces

Solution: False

Because Euclidean geometry is valid only for the figures in the plane but on the curved surfaces, it fails.

Question 2. The boundaries of the solids are curves.

Solution: Because the boundaries of the solids are surfaces.

Question 3. The edges of a surface are curves.

Solution: False

Because the edges of surfaces are lines.

Question 4. The things which are double of the same thing are equal to one another

Solution: True

Since, it is one of the Euclid’s axiom.

Question 5. If a quantity B is a part of another quantity A, then A can be written as the sum of B and some third quantity C.

Solution: True

Since, it is one of the Euclid’s axiom.

Question 6. The statements that are proved are called axioms.

Solution: False

Because the statements that are proved are called theorems.

Question 7. “For every line l and for every point P not lying on a given line l, there exits a unique line m passing though P and parallel to l is known as Playfair’s axiom.

Solution: True

Since, it is an equivalent version of Euclid’s fifth postulate and it is known as Playfair’s axiom.

Question 8. Two distinct intersecting lines cannot be parallel to the same line.

Solution: True

Since, it is an equivalent version of Euclid’s fifth postulate.

Question 9. Attempt to prove Euclid’s fifth postulate using the other postulates and axioms led to the discovery of several other geometries.

Solution: True

All attempts to prove the fifth postulate as a theorem led to a great achievement in the creation of several other geometries. These geometries are quite different from Euclidean geometry and are called non-Euclidean geometry.

NCERT Exemplar Class 9 Maths Chapter 5 Exercise 5.3

Question 1. Two salesmen make equal sales during the month of August. In September, each salesmen doubles his sale of the month of August. Compare their sales in September.

Solution: Let the equal sales of two salesmen in August be y. In September, each salesman doubles his sale of August.

Thus, sale of first salesman is 2y and sale of second salesman is 2y.

According to Euclid’s axioms, things which are double of the same things are equal to one another.

So, in September their sales are again equal.

Question 2.

It is known that x + y = 10 and that x = z. Show that z + y = 10.

Solution:

We have, x + y = 10 …(i)

and x = z …(ii)

On adding y to both sides, we have x + y = z + y …. (iii)

[ ∵ If equals are added to equals, the wholes are equal] From (i) and (iii), we get z + y = 10

Question 3. Look at the given figure. Show that length AH > sum of lengths of AB + BC + CD.

Solution:

From the given figure, we have

AB + BC + CD = AD

[AB, BC and CD are the parts of AD]

Since, AD is also the part of AH.

AH > AD [ ∵ The whole is greater than the part]

So, length AH > sum of lengths of AB + BC + CD.

Question 4. In the given figure, we have AB = BC, BX = BY. Show that AX = CY.

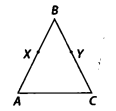
Solution: Given, AB = BC …(i)

and BX = BY …(ii)

On subtracting (ii) from (i), we get AB – BX = BC – BY

[∵ If equals are subtracted from equals, the remainders are equal]

∴ AX = CY

Question 5. In the given figure, we have X and Y are the mid-points of AC and BC and AX = CY. Show that AC = BC.

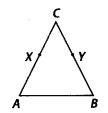
Solution: We have, X is the mid-point of AC.

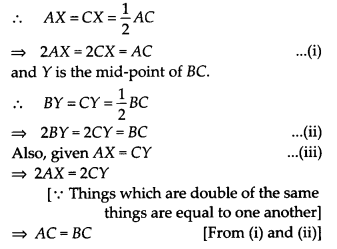
Question 6. In the given figure, we have

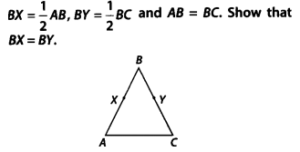
Solution:

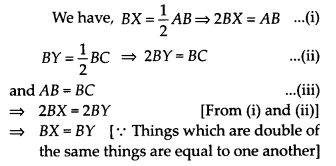
Question 7. In the given figure, we have ∠1 = ∠2 and ∠2 = ∠3. Show that ∠1 = ∠3.

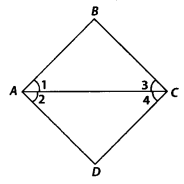
Solution: We have, ∠1 = ∠2 and ∠2 = ∠3 ⇒ ∠1 = ∠3 [ ∵ Things which are equal to the same thing are equal to one another]

Question 8. In the given figure, we have ∠1 = ∠3 and ∠2 = ∠4. Show that ∠A = ∠C.

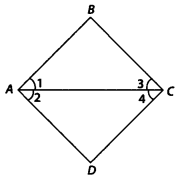
Solution: Given ∠1 = ∠3 …(i)

∠2 = ∠4 …(ii)

Adding (i) and (ii), we get ∠1 + ∠2 = ∠3 + ∠4

[∵ If equals are added to equals, then wholes are also equal]

⇒ ∠A = ∠C

Question 9. In the given figure, we have ∠ABC = ∠ACB, ∠3 = ∠4. Show that ∠1 = ∠2.

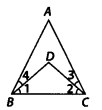
Solution:

Given ∠ABC = ∠ACB …(i)

and ∠A = ∠3 …(ii)

Subtracting (ii) from (i), we get ∠ABC – ∠4 = ∠ACB – ∠3

[ ∵ If equals are subtracted from equals, then remainders are also equal]

⇒ ∠1 = ∠2

Question 10. In the given figure, we have AC = DC, CB = CE. Show that AB = DE.

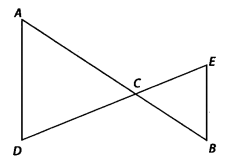
Solution: We have, AC = DC …(i)

and CB = CE …(ii)

Adding (i) and (ii), we get

AC + CB = DC + CE

[ ∵ If equals are added to equals, then wholes are also equal]

⇒ AB = DE

Question 11. In the given figure, if OX = 12XY, PX = 12XZ and OX= PX, show that XY= XZ

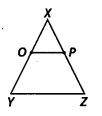
Solution: Given OX = 12XY ⇒ 20X = XY …(i)

PX = 12XZ ⇒ 2PX = XZ …(ii)

and OX = PX …(iii)

multiplying (iii) by 2, we get

2OX = 2PX

[∵ Things which are double of the same things are equal to one another]

⇒ XY = XZ [From (i) and (ii)]

Question 12. In the given figure

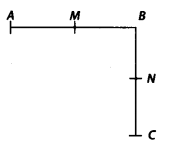
(i) AB = BC, M is the mid-point of AB and N is the mid-point of BC. Show that AM = NC.

(ii) BM = BN, M is the mid-point of AB and N is the mid-point of BC. Show that AB = BC.

Solution:

(i): Given, AB = BC …(1)

M is the mid-point of AB.

and N is the mid-point of BC.

Multiplying both sides of (1) by 12, we get

[ ∵ Things which are halves of the same things are equal to one another]

⇒ AM = NC [Using (2) and (3)]

(ii) Given, BM = BN …(1)

M is the mid-point of AB.

∴ AM = BM = 12AB

⇒ 2AM = 2BM = AB …(2)

and N is the mid-point of BC.

∴ BN = NC = 12BC

⇒ 2BN = 2NC = BC …(3)

multiplying both sides of (1) by 2, we get

2 BM = 2 BN

[ ∵ Things which are double of the same thing are equal to one another]

⇒ AB = BC [Using (2) and (3)]

NCERT Exemplar Class 9 Maths Chapter 5 Exercise 5.4

Question 1. Read the following statement:

An equilateral triangle is a polygon made up of three line segments out of which two line segments are equal to the third one and all its angles are 60° each. Define the terms used in this definition which you feel necessary. Are there any undefined terms in this? Can you justify that all sides and all angles are equal in a equilateral triangle.

Solution: The terms need to be defined are

1. Polygon : A closed figure bounded by three or more line Segments.
2. Line segment : Part of a line with two end points.
3. Line: Undefined term.
4. Point: Undefined term.
5. Angle: A figure formed by two rays with one common initial point.
6. Acute angle : Angle whose measure is between 0° to 90°.

Here undefined terms are line and point. All the angles of equilateral triangle are 60° each (given). Two line segments are equal to the third one (given).

“According to Euclid’s axiom, “things which are equal to the same things are equal to one another”, we conclude that all three sides of an equilateral triangle are equal.

Question 2. Study the following statements:

“Two intersecting lines cannot be perpendicular to the same line.” Check whether it is an equivalent version to the Euclid’s fifth postulate. [Hint: Identify the two intersecting lines / and m and the line n in the above statement.]

Solution: Two equivalent versions of Euclid’s fifth postulate are as follows:

1. For every line l and for every point P not lying on l, there exists a unique line m passing through P and parallel to l.
2. Two distinct intersecting lines cannot be parallel to the same line.

From above two statements it is clear that given statement is not an equivalent version to the Euclid’s fifth postulate.

Question 3. Read the following statements which are taken as axioms:

(i) If a transversal intersects two parallel lines, then corresponding angles are not necessarily equal.

(ii) If a transversal intersect two parallel lines, then alternate interior angles are equal.

Is this system of axioms consistent ? Justify your answer.

Solution:

As we know that, if a transversal intersects two parallel lines, then each pair of corresponding angles are equal, then first is false, so, not an axiom. Also, if a transversal intersects two parallel lines, then each pair of alternate interior angles are equal, then second is true so, it is an axiom.

So, in given statements, first is false and second is an axiom. Thus, given system of axioms is not consistent.

Question 4. Read the following two statements which are taken as axioms:

1. If two lines intersect each other, then the vertically opposite angles are not equal.
2. If a ray stands on a line, then the sum of two adjacent angles, so formed is equal to 180°. Is this system of axioms consistent ? Justify your answer.

Solution: As we know that, if two lines intersect each other, then the vertically opposite angles are equal, then first is false, so, not an axiom. Also, if a ray stands on a line, then the sum of two adjacent angles so formed is equal to 180°, then second is true so, it is an axiom.

So, in given statements, first is false and second is an axiom. Thus, given system of axioms is not consistent.

Question 5. Read the following axioms:

(i) Things which are equal to the same thing are equal to one another.

(ii) If equals are added to equals, the wholes are equal.

(iii) Things which are double of the same thing are equal to one another.

Check whether the given system of axioms is consistent or inconsistent.

Solution: Since, the given three axioms are Euclid’s axioms.

Real-World Applications of Euclid’s Geometry

Euclid’s Geometry is not only theoretical but also finds its applications in the real world:

1. Architecture and Design: Understanding the basic principles of Euclidean geometry is essential in fields like architecture, where shapes and spaces need to be constructed based on geometric principles.
2. Navigation and Mapping: Concepts from Euclidean geometry are still used today in cartography and navigation systems to map out the Earth’s surface.

Including such real-world applications in your study can help you grasp the importance and utility of what you’re learning.

Why Study Euclid’s Geometry with NCERT Exemplar Solutions?

The NCERT Exemplar Solutions for Class 9 Maths Chapter 5 help students:

1. Master Complex Concepts: Euclidean geometry might seem abstract, but our solutions break down the concepts into easy-to-understand steps.
2. Prepare for Competitive Exams: Concepts from Euclid’s Geometry are important not just for school exams but also for competitive exams like JEE.
3. Develop Critical Thinking: Euclid’s approach helps students develop logical reasoning skills which are critical for mathematics as a subject.

Introduction to Euclids Geometry FAQ’s

Is NCERT Exemplar Solutions for Class 9 Maths Chapter 5 suitable for CBSE students?

NCERT Exemplar Solutions have been prescribed for years as a complete source of information to CBSE students, to develop their analytical skills. They have proven to be essential for learning the syllabus and developing the confidence that is required to face their exams. The NCERT Exemplar Solutions for Class 9 Maths Chapter 5 explains the steps with precision, without missing out on essential aspects of solving a question.

Where can I download NCERT Exemplar Solutions for Class 9 Maths Chapter 5?

NCERT Exemplar Solutions for Class 9 Maths Chapter 5 Statistics are provided on the Infinity Learn website, which is considered to be one of the most important study materials for students studying in Class 9. The solutions provided at Infinity Learn are formulated in such a way that every step is explained clearly and in detail. The Solutions for Class 9 Maths NCERT are prepared by the subject experts to help students in their board exam preparation. It is very important for the students to get well versed with these solutions to get a good score in the Class 9 examination.

What is the meaning of Euclidean geometry according to NCERT Exemplar Solutions for Class 9 Maths Chapter 5?

Euclidean geometry is the study of geometrical shapes and figures based on different axioms and theorems. It is basically introduced for flat surfaces. It is better explained especially for the shapes of geometrical figures and planes. By referring to NCERT Exemplar Solutions for Class 9 Maths Chapter 5 students can score well in exams.