CBSE Class 9 Maths Notes Chapter 10 Areas of Parallelograms and Triangles
1. Congruent Figures: Two figures are called congruent if they have the same shape and same size. If two figures X and Y are congruent (see adjoining figure), then using a tracing paper we can superpose one figure over the other such that it will cover the other completely.
So, if two figures X and Y are congruent, they must have equal areas.
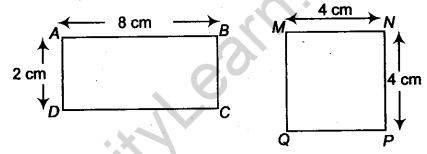
However the converse of this is not true i.e., two figures having equal areas need not be congruent. In adjoining figure, the rectangles ABCD and MNPQ have equal areas (8 × 2 cm2 and 4 × 4 cm2) but clearly, they are not congruent.
2. Area of a figure is a number (in some unit) associated with the part of the plane enclosed by the figure with the following two properties
- If A and B are two congruent figures, then ar (A) = ar(B).
- If a planar region formed by a figure T is made up of two non-overlapping planar regions formed by figures P and Q, then ar(T) = ar(P) + ar(Q)
3. Parallelograms on the same base and between the same parallels are equal in area.
4. A diagonal of a parallelogram divides it into two triangles of equal area.
5. The area of a parallelogram is the product of any of its sides and the corresponding altitude.
6. Triangles on the same base and between the same parallels are equal in area.
7. Area of a triangle = \(\frac { 1 }{ 2 }\) × Base × Height
8. If a triangle and a parallelogram are on the same base and between the same parallels, then the area of the triangle is equal to half the area of the parallelogram.
9. Area of a trapezium = \(\frac { 1 }{ 2 }\) × (Sum of the parallel sides) × (Distance between them)
10. Area of a rhombus = \(\frac { 1 }{ 2 }\) × Product of the diagonals
11. If two triangles have equal areas and one side of the one triangle is equal to one side of the other, then their corresponding altitudes are equal.
12. A median of a triangle divides it into two triangles of equal areas.
13. The line segment joining the mid-points of two sides of a triangle is parallel to the third side. [Mid-point theorem]





