Limits in Maths

In Maths, a limit is defined as a value that a function approaches for the given input. Limits are an important topic in mathematics. It is widely used in Calculus, for Mathematical analysis, to define integrals, derivatives, and continuity.

This article will discuss the Limits in brief along with their types, formulas, and examples.

Limits Definition in Maths

For a real-valued function “f” and a real number “c”, the limit is defined as:

lim_x→c f(x) = L

This definition is read as “the limit of a function of x or “f” of x as x approaches c is equal to L.” The word “lim” represents limit as the right arrow defines that the function approaches the limit as x approaches c.

Limits Definition in Calculus

In calculus, we define a limit as a particular value to which the output of a function approaches the respective input value. It is used in analysis projects and hence, the limit is always concerned with the behavior of the function at a particular point.

The representation of limits in calculus is as follows:

lim_x→c f(x) = L

Also Check – Cube

Limits Types of Integrals

Integrals are generally classified into two types. These are:

• Definite Integrals
• Indefinite Integrals

Definite Integrals

Definite Integrals are defined as the integrals whose upper limit and lower limit are defined properly.

Indefinite Integrals

Indefinite Integrals are the integrals that are expressed without the upper and lower limits. The function will have an arbitrary constant that integrates it.

Limits and Functions

A function may approach two different limits in some cases. These two approaches are:

• The first kind is when the variable approaches its limit through values that are larger than the limit. It is said to be a right-hand limit of the function.
• The second kind is when the variable approaches its limit through values that are smaller than the limit. It is said to be a left-hand limit of the function.

In such cases, a limit is not defined.

The limit of the function will exist if and only if both the right-hand limit and the left-hand limit are equal.

Also Check – Fibonacci Sequence

Limits and Continuity

Limits and continuity are closely related concepts. A function can be either continuous or discontinuous. For a function to be continuous, small changes in the input should result in small changes in the output.

If we say as f(x) → L as x → a, it means that the value of f(x) can get as close as we want to if x is close to a but is not equal to a.

Limits and Derivatives

To find the derivative of a function, f(a) or we can define it as a function at a point a, we use the following formula:

f'(a) = lim_x→a (f(x) – f(a)) / (x – a)

This formula helps us determine how the function changes at a point a.

Limits Formulas

Below is a list of the formulas used to solve the problem related to limits:

• lim_x→a (xⁿ – aⁿ) / (x-a) = na^n-1
• lim_x→0 (e^x – 1) / x = 1
• lim_x→0 (a^x – 1) / x = ln a
• lim_x→0 (ln (1 + x)) / x = 1
• lim_x→0 (log_a(1 + x)) / x = log_ae
• lim_x→0 (sin x) / x = 1
• lim_x→0 (tan x) / x = 1
• lim_x→0 (cos x) / x = 1
• lim_x→0 (sin^-1 x) / x = 1
• lim_x→0 (tan^-1 x) / x = 1
• lim_x→0 (1 + x)^1/x = e
• lim_x→∞ (1 + 1/x)^x = e

Limits Formula PDF

The formula sheets for Limits are important for the students appearing in the class 11th and 12th examinations. You may download the formula charts for Limits from the link below in a PDF Format.

You may also refer to the formula chart for the limits given below:

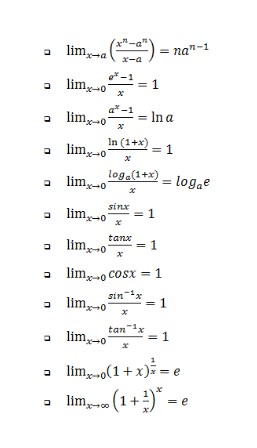
Must See – Average

Limits of Trigonometric Functions

Below is the list of the formulas for the trigonometric functions:

• lim_x→0 (sin x) / x = 1
• lim_x→0 (tan x) / x = 1
• lim_x→0 (cos x) / x = 1
• lim_x→0 (sin^-1 x) / x = 1
• lim_x→0 (tan^-1 x) / x = 1

Limits Properties

Let us assume that lim_x→a f(x) and lim_x→a g(x) exist and let c be a constant. Therefore, below are the properties of the limits:

• lim_x→a (c · f(x)) = c · lim_x→a f(x)
  A constant can be factored out from a limit.
• lim_x→a [f(x) + g(x)] = lim_x→a f(x) + lim_x→a g(x)
  We can add or subtract the limits as per the rule mentioned above.
• lim_x→a [f(x) · g(x)] = lim_x→a f(x) · lim_x→a g(x)
  Similar to the addition and subtraction property discussed above, we follow a similar rule for the multiplication of two or more limits.
• lim_x→a [f(x) / g(x)] = lim_x→a f(x) / lim_x→a g(x), provided that lim_x→a g(x) is not equal to zero.
  Similar to the addition and subtraction property discussed above, we follow a similar rule for the division of two limits.
• lim_x→a c = c
  The limit of a constant is always a constant.
• lim_x→a xⁿ = aⁿ

Limits Practice Questions

1. Check for the limit: limx0(sinx⋅x)
2. Find the limit of the function: limx0(tanx⋅sinx)
3. Evaluate the following limits:
   • limx0(sin2x)
   • limx0(cos2x)
   • limx0(tan2x)
4. Find the limit of the function: limx2(x2+6)
5. Find the limit of the function: limx4(x4+25x)

Limits Maths Practice FAQs

What is a limit in calculus?

A limit describes how a function behaves as the input gets closer to a specific value. It helps us understand the function’s value at that point, even if the function isn’t defined there.

How do you find the limit of a function as x approaches a certain value?

To find the limit of a function f(x) as x approaches a value a, you look at how f(x) behaves as x gets closer to a. This can involve direct substitution, factoring, or other techniques to simplify the function.

What does it mean if the limit does not exist?

If the limit does not exist, it means that as x approaches the value, f(x) does not approach a single, finite number. This can occur if f(x) goes to infinity, oscillates wildly, or behaves unpredictably near the point.