Table of Contents
Introduction to Cone
A cone is a three-dimensional geometric shape that becomes narrow towards the top starting with a flat circular base. The narrow top point is often called the apex or vertex. A cone is a type of pyramid with a circular cross-section. Because of this, it’s often referred to as a circular cone.
This article will discuss the shape of a cone, its properties and its definition in detail.
Definition of a Cone
A cone is formed by connecting a common point, known as the apex or vertex, to all the points on a circular base. The base does not include the apex. The height of the cone is the straight-line distance from the apex to the base. The circular base has a radius, and the slant height is the distance from the apex to any point on the edge of the base.
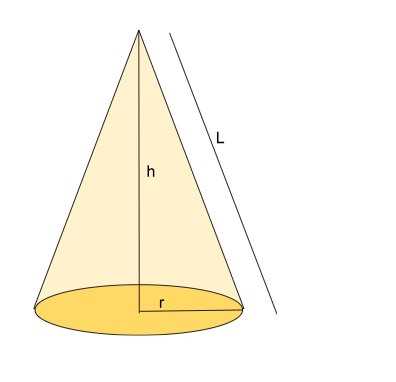
Using these dimensions, you can calculate the cone’s surface area and volume. The key measurements are:
- Height: The height of a cone is the perpendicular distance from the apex to the centre of the base.
- Radius: The radius of the base of the cone is the distance from the centre of the base to any point on its edge.
- Slant Height: The slant height is the distance from the apex to any point on the circumference of the base.
Properties of a Cone
A cone is a three-dimensional shape featuring a curved surface and a circular base. Here are some key properties that define a cone:
- A cone has a base that is always circular.
- A cone has one curved face, one apex (vertex), and no edges.
- The slant height is the distance from the apex to any point on the edge of the base.
- A cone with its apex directly above the centre of its circular base is called a right circular cone.
- A cone where the apex is not directly above the base is known as an oblique cone.
Formulas of Cone
There are three most important formulas related to cones:
- slant height
- surface area
- volume
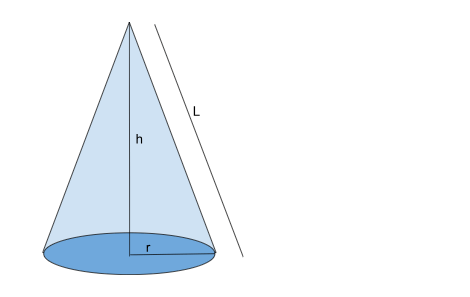
Slant Height
The slant height of a cone can be found using the Pythagorean theorem. If r is the radius of the base and h is the height of the cone, then the slant height l is given by:
l = √r2 + h2
Curved Surface Area
The curved surface area (CSA) of a cone is the area of the cone’s curved part, and it is calculated using the given formula:
Curved Surface Area = πrl
Total Surface Area
The total surface area (TSA) includes both the curved surface area and the area of the base. The formula is:
Total Surface Area = πr2 + πrl
Volume
The volume of a cone is the amount of space it occupies, given by:
volume = 13πr2h
Types of Cones
There are two main types of Cones. Each of these types of cones has distinct characteristics:
Right Circular Cone
A Right Circular Cone features a circular base and an axis that runs perpendicular to this base. The key points about a right circular cone are discussed in the table below.
| Base and Axis | The axis extends vertically from the apex (vertex) to the centre of the base, making a right angle with the base. |
| Vertex Position | The apex is directly above the centre of the base. |
| Common Use | This type is frequently used in geometry and real-world examples like ice cream cones and traffic cones. |
The term “right” refers to the right angle formed between the cone’s axis and its base. The symmetrical and straightforward nature of a right circular cone makes it a fundamental shape in geometry.
Oblique Cone
An Oblique Cone also has a circular base, but its characteristics differ from the right circular cone:
| Base and Axis | The axis of an oblique cone is not perpendicular to the base. It means that the apex is not directly above the centre of the base. |
| Position of the Vertex | The vertex is off-centre relative to the base, giving the cone a slanted look. |
| Appearance | This type of cone appears slanted or tilted compared to the base. |
The oblique cone’s tilt can make it appear less symmetric, and it’s often seen in applications where the slanting design is preferred or necessary.
Frustum of a Cone
A Frustum of a Cone is created when a right circular cone is sliced horizontally or parallel to its base. This cut removes the top portion of the cone, leaving behind the lower section, which is the frustum.
Characteristics of a Frustum of a Cone
- The frustum has two parallel circular bases and a slanted, curved surface connecting these bases.
- The slicing plane is parallel to the base of the cone, creating a truncated cone shape.
Solved Examples of Cone
1. Find the volume of the cone if the radius r = 4cm and the height h = 7cm.
Ans. We can find the volume of the given cone using the following formula: volume = 13r2h
Therefore, substituting r = 4cm and h = 7cm, we get,
volume = 1/3π(4)27
volume = 1/3π(16)7
volume = 1/3(22/7)(16)7
volume = 1/3(352)
volume = 117.333 cubic cm
2. Find the volume of the cone if the radius r = 5cm and the height h = 14cm.
Ans. We can find the volume of the given cone using the following formula: volume = 13r2h
Therefore, substituting r = 5cm and h = 14cm, we get,
volume = 1/3π(5)214
volume = 1/3π(25)14
volume = 1/3(22/7)(25)14
volume = 1/3(1100)
volume = 366.666 cubic cm
Practice Questions of Cone
- 1. Find the volume of the cone if the radius r = 5cm and the height h = 17cm.
- 2. Find the volume of the cone if the radius r = 8cm and the height h = 14cm.
- 3. Find the total surface area of the cone if the radius r = 3cm and the height h = 30cm.
- 4. Find the curved surface area of the cone if the radius r = 6cm and the height h = 52cm.
FAQs on Cone
What is a Cone?
A cone is a three-dimensional geometric shape that consists of a circular base and a curved surface that narrows smoothly to a single point called the apex. This pointed tip at the top of the cone is where all the lines from the base converge.
How Many Faces, Edges, and Vertices Does a Cone Have?
A cone has one face. Also, a cone does not have any edges and has one vertex, which is the apex or the tip of the cone.
What is the Slant Height of a Cone?
The slant height of a cone is the distance from the apex to a point on the edge of the circular base. It is the length along the slant of the cone.
Is a cone a pyramid?
No, a cone is not a pyramid. A cone has a circular base and one curved side that ends in a point, while a pyramid has a polygonal base (like a triangle or square) with flat triangular sides that meet at a single point.
Do cones have faces?
Yes, cones have one face, which is the circular base. The curved surface of a cone is not considered a face because it’s not flat like the faces of a polyhedron.









