Dilation

Dilation refers to resizing an object while maintaining its shape. The size can be increased or decreased depending on the scale factor. Dilation in mathematics is used in geometry to enlarge or shrink two-dimensional and three-dimensional shapes while preserving their proportions. For example, a square with sides of 4 units can be dilated to a square with sides of 40 units, but its shape remains unchanged.

In this article, we will learn more about Dilation, examples of Dilation and more.

Definition of Dilation

Dilation is a geometric transformation that resizes an object by either enlarging or shrinking it, based on a given scale factor. The result is a new figure called the image, while the original figure is called the pre-image.

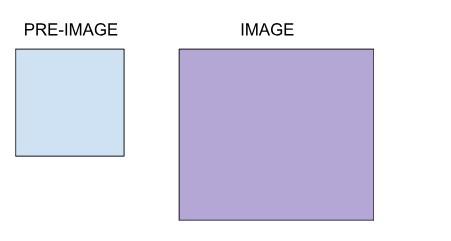
There are two types of dilation:

• Expansion: When the size of the object increases, the object is said to be expanded.
• Contraction: When the size of the object decreases, the object is said to be contracted.

In both cases, the shape of the object remains unchanged.

For example, if a square undergoes dilation, its size may increase or decrease, but its proportions and shape stay consistent.

One Stop Solutions for School Exam Preparation

Boost your school preparation with our comprehensive guide for CBSE, ICSE, and State Board exams. Get all the resources you need in one place and excel in your academic journey. Discover the ultimate one-stop solution at Infinity Learn today!

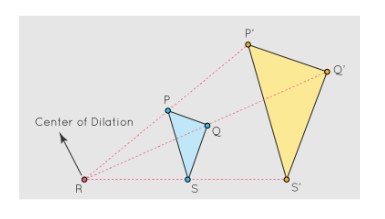
Centre of Dilation

In dilation geometry, the centre of dilation is a key concept. It is the point from which the figure expands or contracts. The resizing of the object occurs relative to this point. If a figure is enlarged or reduced, it stretches or shrinks from the centre of dilation. For example, in a dilation of a triangle, the enlargement or reduction happens from the centre of dilation, marked as point ‘R’ in the figure.

The Scale Factor

The scale factor is the value used to resize a geometric figure in relation to its original size. It represents the ratio between the dimensions of the original figure and the dilated figure.

• If the scale factor (k) is greater than 1 (k > 1), the image enlarges.
• If the scale factor is between 0 and 1 (0 < k < 1), the image contracts.
• If the scale factor is 1 (k = 1), the image remains the same size.
• The scale factor cannot be zero, and its magnitude determines the extent of dilation.

Scale Factor Formula

The scale factor can enlarge or shrink an object. The basic formula to calculate the scale factor of a dilated figure is:

• Scale factor = Dimension of the new shape/Dimension of the original shape
• Alternatively, to find the dimensions of the new shape, you can also use the following formula:
• Dimensions of the original shape × Scale factor = Dimension of the new shape
• This formula helps determine the size of the dilated figure based on the scale factor.

Online Mock Test

Boost Your Preparation With Our Free Online Mock Tests For IIT-JEE, NEET And CBSE Exams

Dilation in Geometry

Dilation in mathematics is the process of resizing an object or shape without altering its proportions or angles. The shape, whether it’s a point, line segment, polygon, etc., can be either enlarged or shrunk. However, the key feature of dilation is that the dimensions of the shape change uniformly, ensuring that its overall proportions and angles remain consistent.

How to Calculate the Scale Factor in Dilation?

Use the original dimension and the modified dimension which then allows for assessment of a scaling factor. Let us work out a triangle’s scaling factor given its original dimensions and enlarged measurements.

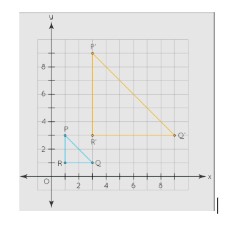
From the above figure, dilation lead to new coordinates of ΔPQR given as follows:

• P(1,3) → P’ (3,9)
• Q(3,1) → Q’ (9,3)
• R(1,1) → R’ (3,3)

Now we can explore each point carefully:

• Vertex P:

The x-coordinate 1 transformed to be 3 while the y-coordinate 3 transformed to be 9. This proves that both of P’s coordinates had their values triplicated in P’.

• Vertex Q:

Contrarily, x-coordinate 3 turned into 9 whereas y-coordinate 1 became 3. This shows that there was the same relationship existing between Q and Q’.

• Vertex R:

The x-coordinate 1 converted to 3 and y-coordinate 1 transformed to be 3 as well. Hence it can be depicted here in that both the position of R’s coordinates had their values of those locations multiplied by three times that of R’.

Thus, this dilation has a scale factor of 3. To create the enlarged Δ PQR’, every coordinate of ΔPQR is multiplied by the scale factor 3. In other words, if k is the scale factor, then (x,y) changes to (kx, ky).

The scale factor can also be computed simply using the formula:

Scale factor = Dimension of new shape ÷ Dimension of the original shape

Hence, in this instance, we can find the scale factor by dividing coordinates of new vertices with the coordinates of original vertices.

Let’s take dimensions of vertex P (1, 3) and P’ (3,9).

• Take the x-coordinate of P’ = 3 and that of P = 1.
• Put them into the formula: 3 ÷ 1 = 3.
• Now, consider the y-coordinate of P’ = 9 and that of P = 3.
• Then, apply to it the same formula 9 ÷ 3 = 3.
• Therefore, we have a scale factor of 3 for both coordinates.

Important Properties Of Dilation

Dilation in geometry preserves certain properties of the original figure while resizing it. Here are a few key properties that remain unchanged:

• Perpendicular and Parallel Lines: The relationships between perpendicular and parallel lines in the original figure are maintained in the dilated image. If lines were parallel or perpendicular before dilation, they remain so afterwards.
• Midpoints of Sides: The midpoints of the sides of the dilated figure correspond to the midpoints of the sides of the original figure. This means that if you find the midpoint of a side in the original shape, the same midpoint relationship will hold in the dilated shape.
• Angles: The angles in the dilated image are equal to the angles in the original figure. The dilation does not alter the measure of any angle in the figure.

Dilation FAQs