Table of Contents
Very Short Answer Type
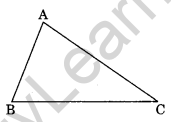
Question 1.
In the given figure, name
(a) the side opposite to vertex A
(b) the vertex opposite A to side AB
(c) the angle opposite to side AC
(d) the angle made by the sides CB and CA.
Solution:
(a) The side opposite to vertex A is BC.
(b) The vertex opposite to side AB is C.
(c) The angle opposite to side AB is ∠ACB.
(d) The angle made by the sides CB and CA is ∠ACB.
Question 2.
Examine whether the given triangles are congruent or not.
Solution:
Here,
AB = DE = 3 cm
BC = DF = 3.5 cm
AC = EF = 4.5 cm
ΔABC = ΔEDF (By SSS rule)
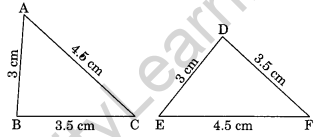
So, ΔABC and ΔEDF are congruent.
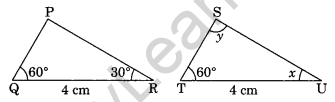
Question 3.
In the given congruent triangles under ASA, find the value of x and y, ΔPQR = ΔSTU.
Solution:
Given: ΔPQR = ΔSTU (By ASA rule)
∠Q = ∠T = 60° (given)
\(\bar { QR }\) = \(\bar { TU }\) = 4 cm (given)
∠x = 30° (for ASA rule)
Now in ΔSTU,
∠S + ∠T + ∠U = 180° (Angle sum property)
∠y + 60° + ∠x = 180°
∠y + 60° + 30° = 180°
∠y + 90° = 180°
∠y = 180° – 90° = 90°
Hence, x = 30° and y = 90°.
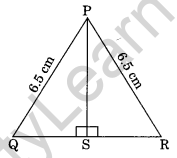
Question 4.
In the following figure, show that ΔPSQ = ΔPSR.
Solution:
In ΔPSQ and ΔPSR
\(\bar { PQ }\) = \(\bar { PR }\) = 6.5 cm (Given)
\(\bar { PS }\) = \(\bar { PS }\) (Common)
∠PSQ = ∠PSR = 90° (Given)
ΔPSQ = ΔPSR (By RHS rule)
Question 5.
Can two equilateral triangles always be congruent? Give reasons.
Solution:
No, any two equilateral triangles are not always congruent.
Reason: Each angle of an equilateral triangle is 60° but their corresponding sides cannot always be the same.
Question 6.
In the given figure, AP = BQ, PR = QS. Show that ΔAPS = ΔBQR
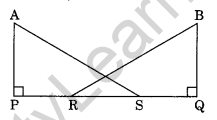
Solution:
In ΔAPS and ΔBQR
AP = BQ (Given)
PR = QS (Given)
PR + RS = QS + RS (Adding RS to both sides)
PS = QR
∠APS = ∠BQR = 90° (Given)
ΔAPS = ΔBQR (by SAS rule)
Question 7.
Without drawing the figures of the triangles, write all six pairs of equal measures in each of the following pairs of congruent triangles.
(i) ΔABC = ADEF
(ii) ΔXYZ = ΔMLN
Solution:
(i) Given: ΔABC = ΔDEF
Here AB = DE
BC = EF
AC = DF
∠A = ∠D, ∠B = ∠E and ∠C = ∠F
(ii) Given ΔXYZ = ΔMLN
Here XY = ML
YZ = LN
XZ = MN
∠X = ∠M, ∠Y = ∠L and ∠Z = ∠N
Question 8.
Lengths of two sides of an isosceles triangle are 5 cm and 8 cm, find the perimeter of the triangle.
Solution:
Since the lengths of any two sides of an isosceles triangle are equal, then
Case I: The three sides of the triangle are 5 cm, 5 cm and 8 cm.
Perimeter of the triangle = 5 cm + 5 cm + 8 cm = 18 cm
Case II: The three sides of the triangle are 5 cm, 8 cm and 8 cm.
Perimeter of the triangle = 5 cm + 8 cm + 8 cm = 21 cm
Hence, the required perimeter is 18 cm or 21 cm.
Question 9.
Write the rule of congruence in the following pairs of congruent triangles.
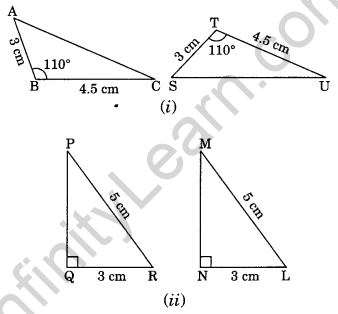
Solution:
(i) Here, AB = ST = 3 cm
BC = TU = 4.5 cm
∠ABC = ∠STU = 110°
ΔABC = ΔSTU (By SAS rule)
(ii) Here ∠PQR = ∠MNL = 90°
hypt. PR = hypt. ML
QR = NL = 3 cm
ΔPQR = ΔMNL (By RHS rule)
Question 10.
In the given figure, state the rule of congruence followed by congruent triangles LMN and ONM.
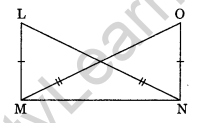
Solution:
In ΔLMN and ΔONM
LM = ON
LN = OM
MN = NM
ΔLMN = ΔONM
Congruence of Triangles Class 7 Extra Questions Short Answer Type
Question 11.
In the given figure, PQR is a triangle in which PQ = PR. QM and RN are the medians of the triangle. Prove that
(i) ΔNQR = ΔMRQ
(ii) QM = RN
(iii) ΔPMQ = ΔPNR
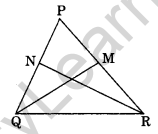
Solution:
ΔPQR is an isosceles triangle. [∵ PQ = PR]
⇒ \(\frac { 1 }{ 2 }\) PQ = \(\frac { 1 }{ 2 }\) PR
⇒ NQ = MR and PN = PM
(i) In ΔNQR and ΔMRQ
NQ = MR (Half of equal sides)
∠NQR = ∠MRQ (Angles opposite to equal sides)
QR = RQ (Common)
ΔNQR = ΔMRQ (By SAS rule)
(ii) QM = RN (Congruent parts of congruent triangles)
(iii) In ΔPMQ and ΔPNR
PN = PM (Half of equal sides)
PR = PQ (Given)
∠P = ∠P (Common)
ΔPMQ = ΔPNR (By SAS rule)
Question 12.
In the given figure, PQ = CB, PA = CR, ∠P = ∠C. Is ΔQPR = ΔBCA? If yes, state the criterion of congruence.
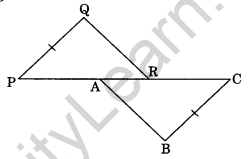
Solution:
Given:
PQ = CB, PA = CR
and ∠P = ∠C
In ΔQPR and ΔBCA,
PQ = CB (Given)
∠QPR = ∠BCA (Given)
PA = CR (Given)
PA + AR = CR + AR (Adding AR to both sides)
or PR = CA
ΔQPR = ΔBCA (By SAS rule)
Question 13.
In the given figure, state whether ΔABC = ΔEOD or not. If yes, state the criterion of congruence.
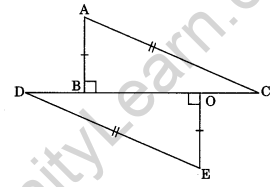
Solution:
In ΔABC and ΔEOD
AB = OE
∠ABC = ∠EOD = 90°
AC = ED
ΔABC = ΔEOD
Hence, ΔABC = ΔEOD
RHS is the criterion of congruence.
Question 14.
In the given figure, PQ || RS and PQ = RS. Prove that ΔPUQ = ΔSUR.
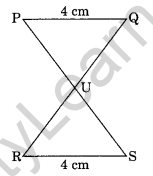
Solution:
In ΔPUQ and ΔSUR
PQ = SR = 4 cm
∠UPQ = ∠USR (Alternate interior angles)
∠PQU = ∠SRU (Alternate interior angles)
ΔPUQ = ΔSUR (By ASA rule)
Congruence of Triangles Class 7 Extra Questions Long Answer Type
Question 15.
In the given figure ΔBAC = ΔQRP by SAS criterion of congruence. Find the value of x and y.
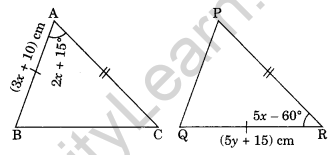
Solution:
Given: ΔBAC = ΔQRP (By SAS rule)
So, BA = QR
⇒ 3x + 10 = 5y + 15 ……(i)
∠BAC = ∠QRP
⇒ 2x + 15° = 5x – 60° ……(ii)
From eq. (ii), we have
2x + 15 = 5x – 60
⇒ 2x – 5x = -15 – 60
⇒ -3x = -7 5
⇒ x = 25
From eq. (i), we have
3x + 10 = 5y + 15
⇒ 3 × 25 + 10 = 5y + 15
⇒ 75 + 10 = 5y + 15
⇒ 85 = 5y + 15
⇒ 85 – 15 = 5y
⇒ 70 = 5y
⇒ y = 14
Hence, the required values of x and y are 25 and 14 respectively.
Question 16.
Observe the figure and state the three pairs of equal parts in triangles ABC and DCB.
(i) Is ΔABC = ΔDCB? Why?
(ii) Is AB = DC? Why?
(iii) Is AC = DB? Why? (NCERT Exemplar)
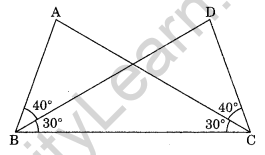
Solution:
(i) In ΔABC and ΔDCB
∠ABC = ∠DCB = 70° (40° + 30° = 70°) (Given)
∠ACB = ∠DCB = 30° (Given)
BC = CB (Common)
ΔABC = ΔDCB (By ASA rule)
(ii) Yes,
AB = DC (Congruent parts of congruent triangles)
(iii) Yes,
AC = DB (Congruent parts of congruent triangles)
Question 17.
In the given figure, ΔQPS = ΔSRQ. Find each value.
(a) x
(b) ∠PQS
(c) ∠PSR
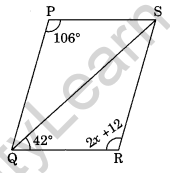
Solution:
(a) ΔQPS = ΔSRQ
∠QPS = ∠SRQ (Congruent part of congruent triangles)
106 = 2x + 12
⇒ 106 – 12 = 2x
⇒ 94 = 2x
⇒ x = 47
∠QRS = 2 × 47 + 12 = 94 + 12 = 106°
So, PQRS is a parallelogram.
∠QSR = 180° – (42° + 106°) = 180° – 148° = 32°
(b) ∠PQS = 32° (alternate interior angles)
(c) ∠PSQ = 180° – (∠QPS + ∠PQS) = 180° – (106° + 32°) = 180° – 138° = 42°
∠PSR = 32° + 42° = 74°
Congruence of Triangles Class 7 Extra Questions Higher Order Thinking Skills (HOTS) Type
Question 18.
In ΔABC, medians BD and CE are equal and intersect each other at O. Prove that ΔABC is an isosceles triangle.
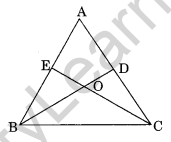
Solution:
We know that the medians of a triangle intersect each other in the ratio 2 : 1.
BD = CE (Given)
\(\frac { 2 }{ 3 }\) BD = \(\frac { 2 }{ 3 }\) CE
⇒ OB = OC
\(\frac { 1 }{ 3 }\) BD = \(\frac { 1 }{ 3 }\) CE
⇒ OE = OD
In ΔBOE and ΔCOD,
OB = OC
OE = OD
∠BOE = ∠COD (Vertically opposite angles)
ΔBOE = ΔCOD (By SAS rule)
BE = CD (Congruent parts of congruent triangles)
2BE = 2CD
⇒ AB = AC
Hence ΔABC is an isosceles triangle.
Question 19.
Prove that the lengths of altitudes drawn to equal sides of an isosceles triangle are also equal.
(i) ∠TRQ = ∠SQR?
(ii) If ∠TRQ = 30°, find the base angles of the ΔPQR.
(iii) Is ΔPQR an equilateral triangle?
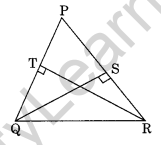
Solution:
In ΔQTR and ΔRSQ
∠QTR = ∠RSQ = 90° (Given)
∠TQR = ∠SRQ (Base angle of an isosceles triangle)
∠QRT = ∠RQS (Remaining third angles)
QR = QR (Common)
ΔQTR = ΔRSQ (By ASA rule)
QS = RT (Congruent parts of congruent triangles)
Hence proved.
(i) ∠TRQ = ∠SQR (Congruent parts of congruent triangles)
(ii) In ΔQTR,
∠TRQ = 30° (Given)
∠QTR + ∠TQR + ∠QRT = 180° (Angle sum property)
⇒ 90° + ∠TQR + 30° = 180°
⇒ 120° + ∠TQR = 180°
⇒ ∠TQR = 180° – 120° = 60°
⇒ ∠TQR = ∠SRQ = 60°
Each base angle = 60°
(iii) In ΔPQR,
∠P + ∠Q + ∠R = 180° (Angle sum property)
⇒ ∠P + 60° + 60° = 180° (From ii)
⇒ ∠P + 120° = 180°
⇒ ∠P = 180° – 120° = 60°
Hence, ΔPQR is an equilateral triangle.



