Algebraic Expressions Class 7 Extra Questions Maths Chapter 12

Algebraic Expressions Class 7 Extra Questions Maths Chapter 12

Extra Questions for Class 7 Maths Chapter 12 Algebraic Expressions

Algebraic Expressions Class 7 Extra Questions Very Short Answer Type

Question 1.
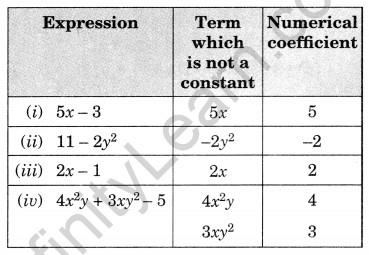
Identify in the given expressions, terms which are not constants. Give their numerical coefficients.
(i) 5x – 3
(ii) 11 – 2y²
(iii) 2x – 1
(iv) 4x²y + 3xy² – 5
Solution:

Question 2.
Group the like terms together from the following expressions:
-8x²y, 3x, 4y, \(\frac { -3 }{ 2 }\)x , 2x²y, -y
Solution:
Group of like terms are:
(i) -8x²y, 2x²y
(ii) 3x, \(\frac { -3 }{ 2 }\)x
(iii) 4y, -y

Question 3.
Identify the pairs of like and unlike terms:
(i) \(\frac { -3 }{ 2 }\)x, y
(ii) -x, 3x
(iii) \(\frac { -1 }{ 2 }\)y2x, \(\frac { 3 }{ 2 }\)xy²
(iv) 1000, -2
Solution:
(i) \(\frac { -3 }{ 2 }\)x, y → Unlike Terms
(ii) -x, 3x → Like Terms
(iii) \(\frac { -1 }{ 2 }\)y2x, \(\frac { 3 }{ 2 }\)xy² → Like Terms
(iv) 1000, -2 → Like Terms

Question 4.
Classify the following into monomials, binomial and trinomials.
(i) -6
(ii) -5 + x
(iii) \(\frac { 3 }{ 2 }\)x – y
(iv) 6x² + 5x – 3
(v) z² + 2
Solution:
(i) -6 is monomial
(ii) -5 + x is binomial
(iii) \(\frac { 3 }{ 2 }\)x – y is binomial
(iv) 6x² + 5x – 3 is trinomial
(v) z² + z is binomial

Question 5.
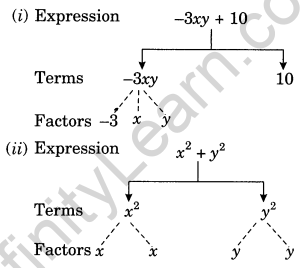
Draw the tree diagram for the given expressions:
(i) -3xy + 10
(ii) x² + y²
Solution:

Question 6.
Identify the constant terms in the following expressions:
(i) -3 + \(\frac { 3 }{ 2 }\)x
(ii) \(\frac { 3 }{ 2 }\) – 5y + y²
(iii) 3x² + 2y – 1
Solution:
(i) Constant term = -3
(ii) Constant term = \(\frac { 3 }{ 2 }\)
(iii) Constant term = -1

Question 7.
Add:
(i) 3x²y, -5x²y, -x²y
(ii) a + b – 3, b + 2a – 1
Solution:
(i) 3x²y, -5x²y, -x²y
= 3x²y + (-5x²y) + (-x²y)
= 3x²y – 5x²y – x²y
= (3 – 5 – 1 )x²y
= -3x²y
(ii) a + b – 3, b + 2a – 1
= (a + b – 3) + (b + 2a – 1)
= a + b – 3 + b + 2a – 1
= a + 2a + b + b – 3 – 1
= 3a + 2b – 4

Question 8.
Subtract 3x² – x from 5x – x².
Solution:
(5x – x²) – (3x² – x)
= 5x – x² – 3x² + x
= 5x + x – x² – 3x²
= 6x – 4x²

Question 9.
Simplify combining the like terms:
(i) a – (a – b) – b – (b – a)
(ii) x² – 3x + y² – x – 2y²
Solution:
(i) a – (a – b) – b – (b – a)
= a – a + b – b – b + a
= (a – a + a) + (b – b – b)
= a – b
(ii) x² – 3x + y² – x – 2y²
= x² + y² – 2y² – 3x – x
= x² – y² – 4x

Algebraic Expressions Class 7 Extra Questions Short Answer Type

Question 10.
Subtract 24xy – 10y – 18x from 30xy + 12y – 14x.
Solution:
(30xy + 12y – 14x) – (24xy – 10y – 18x)
= 30xy + 12y – 14x – 24xy + 10y + 18x
= 30xy – 24xy + 12y + 10y – 14x + 18x
= 6xy + 22y + 4x

Question 11.
From the sum of 2x² + 3xy – 5 and 7 + 2xy – x² subtract 3xy + x² – 2.
Solution:
Sum of the given term is (2x² + 3xy – 5) + (7 + 2xy – x²)
= 2x² + 3xy – 5 + 7 + 2xy – x²
= 2x² – x² + 3xy + 2xy – 5 + 7
= x² + 5xy + 2
Now (x² + 5xy + 2) – (3xy + x² – 2)
= x² + 5xy + 2 – 3xy – x² + 2
= x² – x² + 5xy – 3xy + 2 + 2
= 0 + 2xy + 4
= 2xy + 4

Question 12.
Subtract 3x² – 5y – 2 from 5y – 3x² + xy and find the value of the result if x = 2, y = -1.
Solution:
(5y – 3x² + xy) – (3x² – 5y – 2)
= 5y – 3x² + xy – 3x² + 5y + 2
= -3x² – 3x² + 5y + 5y + xy + 2
= -6x² + 10y + xy + 2
Putting x = 2 and y = -1, we get
-6(2)² + 10(-1) + (2)(-1) + 2
= -6 × 4 – 10 – 2 + 2
= -24 – 10 – 2 + 2
= -34

Question 13.
Simplify the following expressions and then find the numerical values for x = -2.
(i) 3(2x – 4) + x² + 5
(ii) -2(-3x + 5) – 2(x + 4)
Solution:
(i) 3(2x – 4) + x² + 5
= 6x – 12 + x² + 5
= x² + 6x – 7
Putting x = -2, we get
= (-2)² + 6(-2) – 7
= 4 – 12 – 7
= 4 – 19
= -15
(ii) -2(-3x + 5) – 2(x + 4)
= 6x – 10 – 2x – 8
= 6x – 2x – 10 – 8
= 4x – 18
Putting x = -2, we get
= 4(-2) – 18
= -8 – 18
= -26

Question 14.
Find the value of t if the value of 3x² + 5x – 2t equals to 8, when x = -1.
Solution:
3x² + 5x – 2t = 8 at x = -1
⇒ 3(-1)² + 5(-1) – 2t = 8
⇒ 3(1) – 5 – 2t = 8
⇒ 3 – 5 – 2t = 8
⇒ -2 – 2t = 8
⇒ 2t = 8 + 2
⇒ -2t = 10
⇒ t = -5
Hence, the required value of t = -5.

Question 15.
Subtract the sum of -3x³y² + 2x²y³ and -3x²y³ – 5y⁴ from x⁴ + x³y² + x²y³ + y⁴.
Solution:
Sum of the given terms:

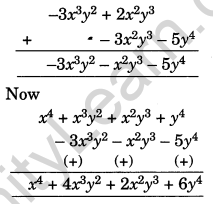
Required expression

Question 16.
What should be subtracted from 2x³ – 3x²y + 2xy² + 3y² to get x³ – 2x²y + 3xy² + 4y²? [NCERT Exemplar] Solution:
We have

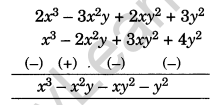
Required expression

Question 17.
To what expression must 99x³ – 33x² – 13x – 41 be added to make the sum zero? [NCERT Exemplar] Solution:
Given expression:
99x³ – 33x² – 13x – 41
Negative of the above expression is
-99x³ + 33x² + 13x + 41
(99x³ – 33x² – 13x – 41) + (-99x³ + 33x² + 13x + 41)
= 99x³ – 33x² – 13x – 41 – 99x³ + 33x² + 13x + 41
= 0
Hence, the required expression is -99x³ + 33x² + 13x + 41

Algebraic Expressions Class 7 Extra Questions Higher Order Thinking Skills (HOTS) Type

Question 18.
If P = 2x² – 5x + 2, Q = 5x² + 6x – 3 and R = 3x² – x – 1. Find the value of 2P – Q + 3R.
Solution:
2P – Q + 3R = 2(2x² – 5x + 2) – (5x² + 6x – 3) + 3(3x² – x – 1)
= 4x² – 10x + 4 – 5x² – 6x + 3 + 9x² – 3x – 3
= 4x² – 5x² + 9x² – 10x – 6x – 3x + 4 + 3 – 3
= 8x² – 19x + 4
Required expression.

Question 19.
If A = -(2x + 3), B = -3(x – 2) and C = -2x + 7. Find the value of k if (A + B + C) = kx.
Solution:
A + B + C = -(2x + 13) – 3(x – 2) + (-2x + 7)
= -2x – 13 – 3x + 6 – 2x + 7
= -2x – 3x – 2x – 13 + 6 + 7
= -7x
Since A + B + C = kx
-7x = kx
Thus, k = -7

Question 20.
Find the perimeter of the given figure ABCDEF.

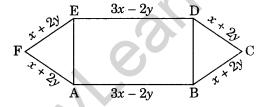
Solution:
Required perimeter of the figure
ABCDEF = AB + BC + CD + DE + EF + FA
= (3x – 2y) + (x + 2y) + (x + 2y) + (3x – 2y) + (x + 2y) + (x + 2y)
= 2(3x – 2y) + 4(x + 2y)
= 6x – 4y + 4x + 8y
= 6x + 4x-4y + 8y
= 10x + 4y
Required expression.

Question 21.
Rohan’s mother gave him ₹ 3xy² and his father gave him ₹ 5(xy² + 2). Out of this total money he spent ₹ (10 – 3xy²) on his birthday party. How much money is left with him? [NCERT Exemplar] Solution:
Money give by Rohan’s mother = ₹ 3xy²
Money given by his father = ₹ 5(xy² + 2)
Total money given to him = ₹ 3xy² + ₹ 5 (xy² + 2)
= ₹ [3xy² + 5(xy² + 2)] = ₹ (3xy² + 5xy² + 10)
= ₹ (8xy² + 10).
Money spent by him = ₹ (10 – 3xy)²
Money left with him = ₹ (8xy² + 10) – ₹ (10 – 3xy²)
= ₹ (8xy² + 10 – 10 + 3x²y)
= ₹ (11xy²)
Hence, the required money = ₹ 11xy²