Table of Contents
Exponents and Powers Class 7 Extra Questions Maths Chapter 13
Extra Questions for Class 7 Maths Chapter 13 Exponents and Powers
Exponents and Powers Class 7 Extra Questions Very Short Answer Type
Question 1.
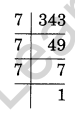
Express 343 as a power of 7.
Solution:
We have 343 = 7 × 7 × 7 = 73
Thus, 343 = 73
Question 2.
Which is greater 32 or 23?
Solution:
We have 32 = 3 × 3 = 9
23 = 2 × 2 × 2 = 8
Since 9 > 8
Thus, 32 > 23
Question 3.
Express the following number as a powers of prime factors:
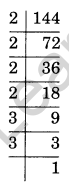
(i) 144
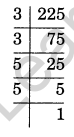
(ii) 225
Solution:
(i) We have
144 = 2 × 2 × 2 × 2 × 3 × 3 = 24 × 32
Thus, 144 = 24 × 32
(ii) We have
225 = 3 × 3 × 5 × 5 = 32 × 52
Thus, 225 = 32 × 52
Question 4.
Find the value of:
(i) (-1)1000
(ii) (1)250
(iii) (-1)121
(iv) (10000)0
Solution:
(i) (-1)1000 = 1 [∵ (-1)even number = 1]
(ii) (1)250 = 1 [∵ (1)even number = 1]
(iii) (-1)121 = -1 [∵ (-1)odd number = -1]
(iv) (10000)0 = 1 [∵ a0 = 1]
Question 5.
Express the following in exponential form:
(i) 5 × 5 × 5 × 5 × 5
(ii) 4 × 4 × 4 × 5 × 5 × 5
(iii) (-1) × (-1) × (-1) × (-1) × (-1)
(iv) a × a × a × b × c × c × c × d × d
Solution:
(i) 5 × 5 × 5 × 5 × 5 = (5)5
(ii) 4 × 4 × 4 × 5 × 5 × 5 = 43 × 53
(iii) (-1) × (-1) × (-1) × (-1) × (-1) = (-1)5
(iv) a × a × a × b × c × c × c × d × d = a3b1c3d2
Question 6.
Express each of the following as product of powers of their prime factors:
(i) 405
(ii) 504
(iii) 500
Solution:
(i) We have
405 = 3 × 3 × 3 × 3 × 5 = 34 × 51
Thus, 405 = 34 × 51
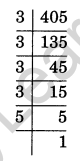
(ii) We have
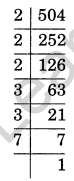
504 = 2 × 2 × 2 × 3 × 3 × 7 = 23 × 32 × 71
Thus, 504 = 23 × 32 × 71
(iii) We have
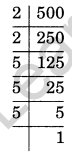
500 = 2 × 2 × 5 × 5 × 5 = 22 × 53
Thus, 500 = 22 × 53
Question 7.
Simplify the following and write in exponential form:
(i) (52)3
(ii) (23)3
(iii) (ab)c
(iv) [(5)2]2
Solution:
(i) (52)3 = 52×3 = 56
(ii) (23)3 = 23×3 = 29
(iii) (ab)c = ab×c = abc
(iv) [(5)2]2 = 52×2 = 54
Question 8.
Verify the following:
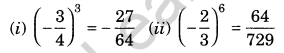
Solution:

Question 9.
Simplify:
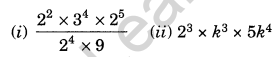
Solution:
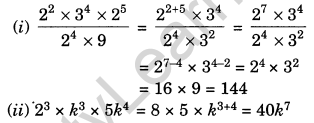
Question 10.
Simplify and write in exponential form:
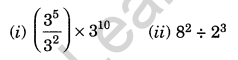
Solution:
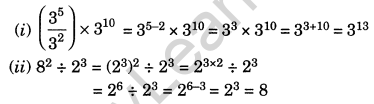
Exponents and Powers Class 7 Extra Questions Short Answer Type
Question 11.
Express each of the following as a product of prime factors is the exponential form:
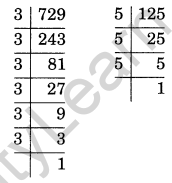
(i) 729 × 125
(ii) 384 × 147
Solution:
(i) 729 × 125 = 3 × 3 × 3 × 3 × 3 × 3 × 5 × 5 × 5 = 36 × 53
Thus, 729 × 125 = 36 × 53
(ii) 384 × 147 = 2 × 2 × 2 × 2 × 2 × 2 × 2 × 3 × 3 × 7 × 7 = 27 × 32 × 72
Thus, 384 × 147 = 27 × 32 × 72
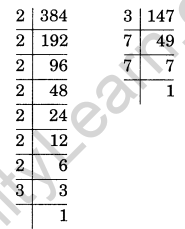
Question 12.
Simplify the following:
(i) 103 × 90 + 33 × 2 + 70
(ii) 63 × 70 + (-3)4 – 90
Solution:
(i) 103 × 90 + 33 × 2 + 70
= 1000 + 54 + 1
= 1055
(ii) 63 × 70 + (-3)4 – 90
= 216 × 1 + 81 – 1
= 216 + 80
= 296
Question 13.
Write the following in expanded form:
(i) 70,824
(ii) 1,69,835
Solution:
(i) 70,824
= 7 × 10000 + 0 × 1000 + 8 × 100 + 2 × 10 + 4 × 100
= 7 × 104 + 8 × 102 + 2 × 101 + 4 × 100
(ii) 1,69,835
= 1 × 100000 + 6 × 10000 + 9 × 1000 + 8 × 100 + 3 × 10 + 5 × 100
= 1 × 105 + 6 × 104 + 9 × 103 + 8 × 102 + 3 × 101 + 5 × 100
Question 14.
Find the number from each of the expanded form:
(i) 7 × 108 + 3 × 105 + 7 × 102 + 6 × 101 + 9
(ii) 4 × 107 + 6 × 103 + 5
Solution:
(i) 7 × 108 + 3 × 105 + 7 × 102 + 6 × 101 + 9
= 7 × 100000000 + 3 × 100000 + 7 × 100 + 6 × 10 + 9
= 700000000 + 300000 + 700 + 60 + 9
= 700300769
(ii) 4 × 107 + 6 × 103 + 5
= 4 × 10000000 + 6 × 1000 + 5
= 40000000 + 6000 + 5
= 40006005
Question 15.
Find the value of k in each of the following:
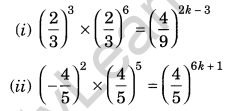
Solution:


Question 16.
Find the value of
(a) 30 ÷ 40
(b) (80 – 20) ÷ (80 + 20)
(c) (20 + 30 + 40) – (40 – 30 – 20)
Solution:
(a) We have 30 ÷ 40 = 1 ÷ 1 = 1 [∵ a0 = 1]
(6) (80 – 20) ÷ (80 + 20) = (1 – 1) ÷ (1 + 1) = 0 ÷ 2 = 0
(c) (20 + 30 + 40) – (40 – 30 – 20)
= (1 + 1 + 1) – (1 – 1 – 1) [∵ a0 = 1]
= 3 – 1
= 2
Question 17.
Express the following in standard form:
(i) 8,19,00,000
(ii) 5,94,00,00,00,000
(iii) 6892.25
Solution:
(i) 8,19,00,000 = 8.19 × 107
(ii) 5,94,00,00,00,000 = 5.94 × 1011
(iii) 6892.25 = 6.89225 × 103
Question 18.
Evaluate:
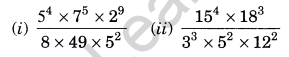
Solution:

Exponents and Powers Class 7 Extra Questions Higher Order Thinking Skills (HOTS) Type
Question 19.
Find the value of x, if
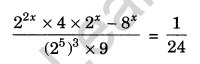
Solution:
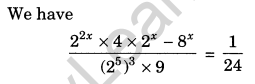

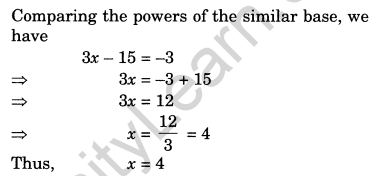
Question 20.
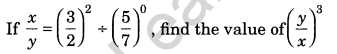
Solution:








