Table of Contents
Cube and cube roots are fundamental concepts in Class 8 maths. These concepts help us solve problems by finding the cube of a number and the cube root of a number. In this section, we have extra questions on cube and cube roots to help you practice and improve your skills.
These extra questions Cube and cube roots in Class 8 maths are designed to be challenging yet manageable, allowing you to develop your critical thinking and problem-solving skills. By working through these questions, you will gain a deeper understanding of the importance of cube and cube roots class 8 extra questions in real-life applications and develop a strong foundation for future mathematical studies.
Extra Questions for Class 8 Maths Chapter 7 Cubes and Cube Roots
Explore the concepts of extra questions cubes and cube roots for Class 8. These concepts are crucial for solving various mathematical problems. Here, we have extra questions to help you practice and improve your skills in finding cubes and cube roots.
Cubes and Cube Roots Class 8 Extra Questions Very Short Answer Type
Ques: Find the cubes of the following:
(a) 12
(b) -6
(c) \(\frac { 2 }{ 3 }\)
(d) \(\frac { -5 }{ 6 }\)
Solution:
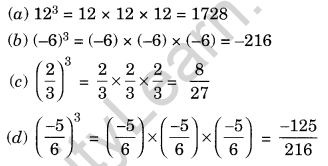
Ques: Find the cubes of the following:
(a) 0.3
(b) 0.8
(c) .001
(d) 2 – 0.3
Solution.
(a) (0.3)3 = 0.3 × 0.3 × 0.3 = 0.027
(b) (0.8)3 = 0.8 × 0.8 × 0.8 = 0.512
(c) (0.001)3 = (0.001) × (0.001) × (0.001) = 0.000000001
(d) (2 – 0.3)3 = (1.7)3 = 1.7 × 1.7 × 1.7 = 4.913
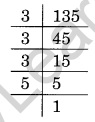
Ques: Is 135 a perfect cube?
Solution:
Prime factorisation of 135, is:
135 = 3 × 3 × 3 × 5
We find that on making triplet, the number 5 does not make a group of the triplet.
Hence, 135 is not a perfect cube.
Ques: Find the cube roots of the following:
(a) 1728
(b) 3375
Solution:


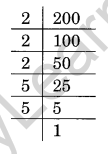
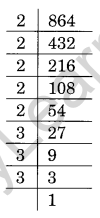
Ques: Examine if (i) 200 (ii) 864 are perfect cubes.
Solution:
(i) 200 = 2 × 2 × 2 × 5 × 5
If we form triplet of equal factors, the number 2 forms a group of three whereas 5 does not do it.
Therefore, 200 is not a perfect cube.
(ii) We have 864 = 2 × 2 × 2 × 2 × 2
If we form triplet of equal factors, the number 2 and 3 form a group of three whereas another group of 2’s does not do so.
Therefore, 864 is not a perfect cube.
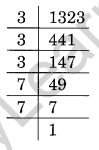
Ques: Find the smallest number by which 1323 may be multiplied so that the product is a perfect cube.
Solution:
1323 = 3 × 3 × 3 × 7 × 7
Since we required one more 7 to make a triplet of 7.
Therefore 7 is the smallest number by which 1323 may be multiplied to make it a perfect cube.
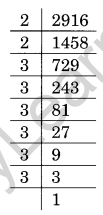
Ques: What is the smallest number by which 2916 should be divided so that the quotient is a perfect cube?
Solution:
Prime factorisation of
2916 = 2 × 2 × 3 × 3 × 3 × 3 × 3 × 3
Since we required one more 2 to make a triplet
Therefore, the required smallest number by which 2916 should be divided to make it a perfect cube is 2 × 2 = 4, i.e., 2916 ÷ 4 = 729 which is a perfect cube.
Ques: Check whether 1728 is a perfect cube by using prime factorisation. (NCERT Exemplar)
Solution:
Prime factorisation of 1728 is
1728 = 2 × 2 × 2 × 2 × 2 × 2 × 3 × 3 × 3
Since all prime factors can be grouped in triplets.
Therefore, 1728 is a perfect cube.
Ques: Using prime factorisation, find the cube root of 5832. (NCERT Exemplar)
Solution:

Ques:
![]()
Solution:

Cubes and Cube Roots Class 8 Extra Questions Short Answers Type
Ques:
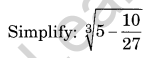
Solution:
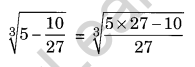
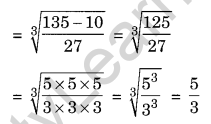
Ques: Find the cube roots of
(i) 4\(\frac { 12 }{ 125 }\)
(ii) -0.729
Solution:

Ques: Express the following numbers as the sum of odd numbers using the given pattern

Solution:
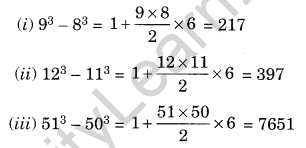
Ques: Observe the following pattern and complete the blank spaces.
13 = 1
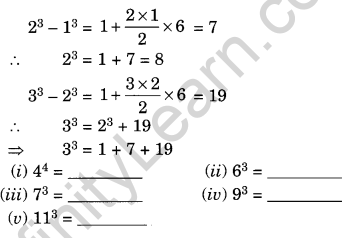
Solution: