Square Root Formula 

Introduction:

The square root is a mathematical operation that involves finding the value which, when multiplied by itself, gives a given number. It is denoted by the symbol √. Square roots are commonly used in various mathematical and scientific calculations, such as solving equations, measuring distances, and determining the sides of geometric shapes. They play a fundamental role in understanding and manipulating numbers in many areas of mathematics and beyond.

What is square root?

In mathematics, the square root of a number is a value that, when multiplied by itself, gives the original number. It is the inverse operation of the square.

For example,

The square of 4 is 16. Thus, the square root of 16 is 4.

How to represent a square root?

The square root is represented by the symbol, √ , also known as the radical.

The number inside this symbol is called the Radicand or Base.

For example,

The square root of 16, is written as √16.

How to find the square root of a number in exponential form?

To find the square root of a number in exponential form, keep the base the same and halve

the exponent.

For example,

To find √2

4, we keep the base the same, which is 2, and halve the exponent. So, half of 4,

which is 2.

So, √2

4 = 2

2 = 4.

Let us verify this.

2

4 = 16

∴ √2

4 = √16

∴ √2

4 = 4

How to find the square root of a number by prime factorization?

Let us understand the following steps of the prime factorization method by finding the

square root of 225.

Step 1: Find the prime factors.

Step 2: Make pairs of the same prime factors.

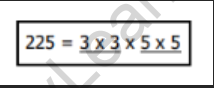
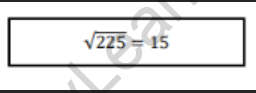
Step 3: Choose one number from each pair and multiply.

Step 4: The result in step 3 is the square root.

How to find the square root of a number by long division?

The long division method is used to find the square root of large numbers usually.

Let us understand the steps in this method by finding the square root of 8281.

Step 1: Write the division as shown below:

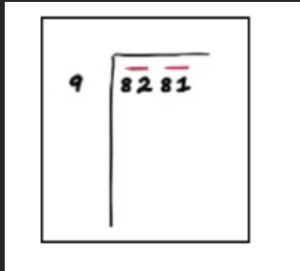
Step 2: Mark pairs of digits from the units end.

Here, the pairs are 81 and 82.

Step 3: Find a perfect square equal to or just lower than the first pair from the left. Write

the square root of this number to the left.

Here, the first pair is 82.

The perfect square lower and closest to 82 is 81.

92 = 81.

So, write the number 9 to the left of 8281.

Step 4: Multiply above and add below the same number.

Multiply 9 with 9 and write the product, that is 81, below 82.

Add 9 with 9 and write the sum, that is 18, on the left side.

Step 5: Draw a box next to the sum. Subtract the product from the number above it.

Here, draw a box next to 18 and subtract 81 from 82. This gives 1.

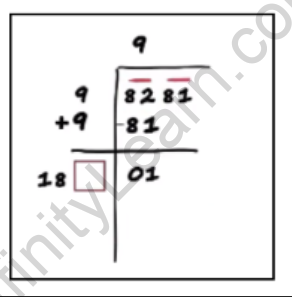
Step 6: Bring the next pair down.

The next pair is 81. Bring it down and write it next to 1.

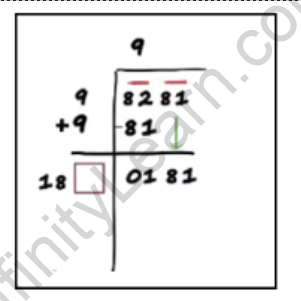
Step 7: Draw a box above and below as shown.

Here, draw a box next to 9 and another box below the box from step 5.

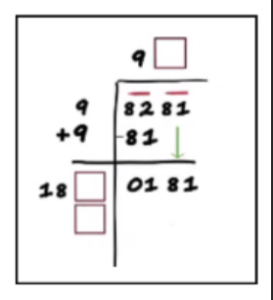
Step 8: Find a number to fill the boxes such that the product on the left gives the result

equal to or less than the number on the right. Use trial and error to find the digit in the

boxes. The number is the same in all the boxes.

Here, we need to find the number, such that the product we get will be less than or equal to 181.

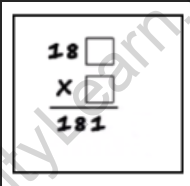
In this case it is 1, as 181 × 1 = 181.

Step 9: Multiply above and add below.

Multiply by 1 and add 1. The product is 181 and the sum is 182.

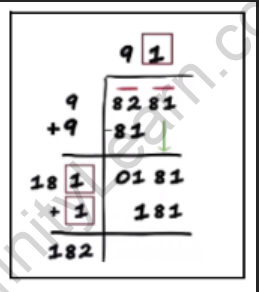
Step 10: Subtract the product from the number above it.

Subtracting 181 from 181 gives 0.

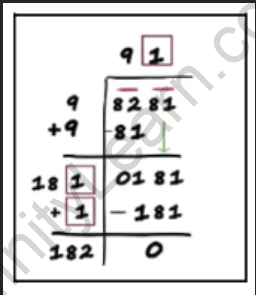
Step 11: Repeat the above process till 0 is obtained and no more pairs are left. Then the

long division stops.

The number on top of the division is the square root.

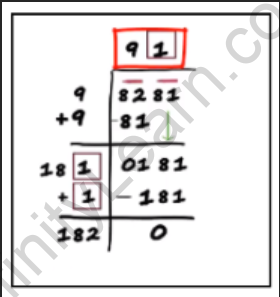
Here, √8281 = 91

The final sum on the left of the long division is always twice the number on the top.

In this case, 182 = 2 × 91.

Solved Examples on Square Root Formula:

Example 1: Find the square root of 11025.

Solution:

Step 1: Find the prime factors of 11025.

∴ 11025 = 3 x 3 x 5 x 5 x 7 x 7

Step 2: Pair the prime factors.

11025 = 3 x 3 x 5 x 5 x 7 x 7

Step 3: Choose one number from each pair and multiply.

11025 = 3 x 5 x 7 = 105

Step 4: The product in step 3 is the square root of 11025.

√11025 = 105

Example 2: Find the square root of 144 using prime factorization.

Solution:

Step 1: Prime factorize 144.

144 = 2x2x2x2x3x2

Step 2: Take the square root of each prime factor.

√2×2x2×2x3×2 = 12

Step 3: Simplify the expression.

√144 = 12

Therefore, the square root of 144 is 12.

Frequently Asked Questions on Square Root Formula:

1: What is a square root?

Answer: A square root is a value that, when multiplied by itself, gives the original number. It is the inverse operation of squaring.

2: How to find square root using prime factorization?

Answer: To find the square root of a number using prime factorization, follow these steps:

1. Prime factorize the given number by breaking it down into its prime factors.

1. Group the prime factors in pairs, each representing the same factor.

1. Take one factor from each pair and write them outside the square root sign.

1. Multiply the factors written outside the square root sign.

1. If any factor is left unpaired, write it inside the square root sign.

1. Simplify the expression if possible.

3: Is a square always positive?

Answer: Yes, a square is always positive or zero. When you square a number (multiply it by itself), the result is either positive or zero. Negative numbers do not have real square roots, as the square of a real number cannot be negative.

4: What are the properties of square roots?

Answer: Some properties of square roots include: the square root of a product is the product of the square roots, the square root of a quotient is the quotient of the square roots, and the square root of a squared value is the absolute value of the original value.

5: Can I approximate square roots without using a calculator?

Answer: Yes, you can approximate square roots without a calculator using techniques such as prime factorization, estimation, or using known square roots as reference points. These methods provide reasonable approximations of square roots.

6: What is a √ in math?

Answer: In mathematics, the symbol √ represents the square root operation. It is used to denote the principal square root of a number. When a number is written as √x, it means finding the value that, when multiplied by itself, gives x. For example, √25 equals 5, as 5 multiplied by itself is 25. The square root symbol (√) is widely used in various mathematical equations and calculations involving roots, exponents, and quadratic functions.

7: Is there a square root of zero?

Answer: Yes, the square root of zero is zero. When you multiply zero by itself, the result is also zero. Therefore, the square root of zero is zero.

8: Is 25 a perfect square?

Answer: Yes, 25 is a perfect square. A perfect square is a number that can be expressed as the square of an integer. In the case of 25, it is equal to 5 raised to the power of 2, which is 52 = 25.