Table of Contents
Introduction to Gradient
Calculus’s foundational idea of gradient assesses how quickly a function changes in relation to its variables. It is essential for comprehending how functions behave and streamlining various procedures. The gradient, its definition, directional derivative, attributes, problem-solving strategies, and frequently asked questions are all covered in this article..
Definition of Gradient
The vector pointing in the direction of the sharpest ascent or descent at any given position is represented by the gradient of a function. It is represented by the symbol (nabla) and is described as the vector of the function’s partial derivatives with respect to each variable.
In mathematics, the gradient f of a function f(x1, x2, x3,…,xn) is denoted by: ∇f and it is equal to
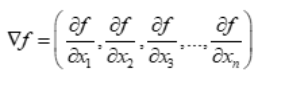
Directional derivative
The directional derivative calculates how quickly a function shifts in a certain direction. It is created by taking the gradient vector’s dot product and the direction-representative unit vector.
The following formulas yield the directional derivative of a function f in the direction of a unit vector u:
Df(u) = ∇f . u = |∇f| |u| cosθ
where ∇f denotes the gradient of f, u is the unit vector, |u| denotes the magnitude of the unit vector, and θ denotes the angle between |f| and |u|.
Properties of Gradient
- The gradient is always pointing in the direction of the function’s steepest increase.
- The gradient’s strength indicates how quickly the function is changing in that direction.
- When the gradient is zero, a critical point (the maximum, minimum, or saddle point) is present.
- The gradient is in opposition to the function’s level curves or surfaces.
Problems on Gradient
Finding the gradient of the function f(x, y) = x2 + 3xy – 2y2 at the position (2,-1) is problem number one.
Solution: We compute the partial derivatives with respect to x and y to determine the gradient:
∂f/∂x = 2x + 3y, ∂f/∂x = 3x – 4y
The coordinates of the point (2, -1) are substituted as follows:
∂f/∂x = 1, ∂f/∂x = 10
Therefore, the gradient of the curve at the point As a result, (2, -1) is ∇f = (1, 10)
Frequently asked questions about Gradient
What does the gradient's geometric meaning entail?
The steepest rise or decline on a surface or in space is indicated by the gradient.
How do a function's level curves and gradient relate to one another?
The gradient and the level curves are always parallel. It indicates the direction of the function's greatest rate of change.
A maximum or minimum point can have a gradient of zero.
The gradient is zero at a maximum or minimum location.
How can the gradient be applied to issues with optimisation?
The gradient is utilised in optimisation to identify important locations when the function is optimised.
What connection does the gradient have to the directional derivative?
The vector that indicates the direction of the highest directional derivative is called the gradient.
What in calculus is the gradient?
The gradient in calculus is the vector of a function's partial derivatives. It indicates the direction of the function's steepest ascent or descent at any given time.
How does optimisation employ the gradient?
The gradient is essential to optimisation since it aids in identifying key locations where the function is optimised. It directs the lookup for a function's maximum or minimum values.
What connection does the gradient curve have to the level curve?
A function's level curves are always orthogonal (perpendicular) to the gradient. It indicates the direction of the function's greatest rate of change.
A maximum or minimum point can have a gradient of zero.
The gradient is 0 at the maximum and minimum points of a function, respectively. This happens because at that certain point, the function has achieved a peak or a valley.
How does vector calculus use the gradient?
In vector calculus, the gradient is used to determine a scalar field's maximum rate of change or direction of change. It is essential for understanding vector fields and how they behave.









