Get Free NCERT Solutions for Class 10 Maths Chapter 2 Ex 2.4 PDF. Polynomials Class 10 Maths NCERT Solutions are extremely helpful while doing homework. Exercise 2.4 Class 10 Maths NCERT Solutions were prepared by Experienced LearnCBSE.in Teachers. Detailed answers of all the questions in Chapter 2 maths class 10 Polynomials Exercise 2.4 provided in NCERT TextBook.
Topics and Sub Topics in Class 10 Maths Chapter 2 Polynomials:
| Section Name | Topic Name |
| 2 | Polynomials |
| 2.1 | Introduction |
| 2.2 | Geometrical Meaning Of The Zeroes Of A Polynomial |
| 2.3 | Relationship Between Zeroes And Coefficients Of A Polynomial |
| 2.4 | Division Algorithm For Polynomials |
| 2.5 | Polynomials |
| 2.6 | Summary |
You can also download the free PDF of Ex 2.4 Class 10 Polynomials NCERT Solutions or save the solution images and take the print out to keep it handy for your exam preparation.
| Board | CBSE |
| Textbook | NCERT |
| Class | Class 10 |
| Subject | Maths |
| Chapter | Chapter 2 |
| Chapter Name | Polynomials |
| Exercise | Ex 2.4 |
| Number of Questions Solved | 5 |
| Category |
NCERT Solutions For Class 10 Maths Chapter 2 Ex 2.4
Ex 2.4 Class 10 Maths Question 1.
Verify that the numbers given alongside of the cubic polynomials below are their zeroes. Also, verify the relationship between the zeroes and the coefficients in each case:
(i) 2x3 + x2 – 5x + 2; \(\frac { 1 }{ 4 }\), 1, -2
(ii) x3 – 4x2 + 5x – 2; 2, 1, 1
Solution:

Ex 2.4 Class 10 Maths Question 2.
Find a cubic polynomial with the sum, some of the product of its zeroes taken two at a time, and the product of its zeroes as 2, -7, -14 respectively.
Solution:
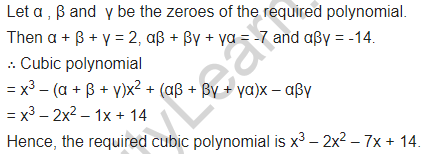
Ex 2.4 Class 10 Maths Question 3.
If the zeroes of the polynomial x3 – 3x2 + x + 1 are a-b, a, a + b, find a and b.
Solution:

Ex 2.4 Class 10 Maths Question 4.
If two zeroes of the polynomial x4 – 6x3 – 26x2 + 138x – 35 are 2 ± √3, find other zeroes.
Solution:

Ex 2.4 Class 10 Maths Question 5.
If the polynomial x4 – 6x3 + 16x2 – 25x + 10 is divided by another polynomial x2 – 2x + k, the remainder comes out to be x + a, find k and a.
Solution:






