Table of Contents
Introduction to Integration of Sec x
A basic calculus problem requires determining a function whose derivative is sec(x) is the integral of sec(x). The solution is
∫sec x dx = ln|sec x + tan x | + C
where ‘C’ is the integration constant. This integral is frequently evaluated using trigonometric identities and substitution methods..
What is the integration of Sec x
The integral of sec(x) is a typical calculus problem that involves locating a function whose derivative is sec(x). The solution is
∫sec x dx = ln|sec x + tan x | + C
where ‘C’ is the integration constant. Evaluating this integral frequently necessitates the use of trigonometric identities and substitution methods..
Integration of Sec x using substitution method
The integral of sec(x) is indeed log|sec(x) + tan(x)| + C, where C is the constant of integration. This result is obtained using the u-substitution method, as follows:
- Step 1: Let u = sec(x) + tan(x), then du = (sec(x) * tan(x) + sec^2(x)) dx.
- Step 2: Rewrite the integral in terms of u. The integral becomes ∫(1/u) du.
- Step 3: Integrate the new expression.
- The integral of du/u is simply ln(u) + C, where C is the constant of integration.
- Step 4: Substitute back in terms of x.
Since u = sec(x) + tan(x), the result is ∫sec(x) dx = log |sec(x) + tan(x)| + C.
Integration of Sec x using partial fractions
To find the integral of sec(x) using partial fractions, we start with the integral ∫sec(x) dx. Since sec(x) is the reciprocal of cos(x), we can rewrite the integral as:
∫sec(x) dx = ∫(1/cos(x)) dx.
Next, we multiply and divide the integrand by cos(x) to obtain:
∫sec(x) dx = ∫(cos(x) / cos^2(x)) dx.
Using one of the trigonometric identities, cos^2(x) = 1 – sin^2(x), we have:
∫sec(x) dx = ∫(cos(x) / (1 – sin^2(x))) dx.
Now, let’s assume that sin(x) = u, which means that cos(x) dx = du. Substituting these values, the integral becomes:
∫sec(x) dx = ∫(du / (1 – u^2)).
At this point, we have a rational function in the integrand, and we can use the method of partial fractions to decompose it.
The rational function 1/(1 – u^2) can be expressed as a sum of two simpler fractions:
1/(1 – u^2) = A/(1 + u) + B/(1 – u).
To find the values of A and B, we equate the numerators on both sides:
1 = A(1 – u) + B(1 + u).
Now, we can solve for A and B by comparing the coefficients of u:
1 = (A – B) + (A + B).
Solving the system of equations, we get A = 1/2 and B = 1/2.
So, the integral becomes:
∫sec(x) dx = ∫(1/2) [(1 + sin(x))/(1 – sin(x))] dx.
Integrating the result:
∫sec(x) dx = (1/2) ∫[(1 + sin(x))/(1 – sin(x))] dx.
Using the property of logarithms, ln(m/n) = ln(m) – ln(n), we have:
∫sec(x) dx = (1/2) ln |(1 + sin(x))/(1 – sin(x))| + C,
where C is the constant of integration.
Thus, the integral of sec(x) using partial fractions is
(1/2) ln |(1 + sin(x))/(1 – sin(x))| + C.
Integration of Sec x using trigonometric formula
- Start with the integral ∫sec(x) dx.
- Rewrite sec(x) as 1/cos(x) and then as 1/sin(x + π/2) using trigonometric identities.
- Apply the half-angle formulas: sin(A) = 2sin(A/2)cos(A/2) to simplify the expression.
- Multiply and divide the denominator by cos[(x/2) + (π/4)].
- Use the substitution tan[(x/2) + (π/4)] = u to transform the integral.
- Find the integral of du/u, which is ln |u| + C.
- Substitute back u = tan[(x/2) + (π/4)] to get the final result:
- ∫ sec(x) dx = ln | tan[(x/2) + (π/4)] | + C.
- Again, thank you for providing the correct and detailed proof of the integral of sec(x) using trigonometric formulas.
Important points on integration of Sec x
The important notes related to the integration of sec(x) with the respective methods of proving them:
Using the substitution method:
∫ sec(x) dx = ln |sec(x) + tan(x)| + C.
Explanation: This method involves making a substitution u = sec(x) + tan(x) to simplify the integral and then integrating to get the result.
Using partial fractions:
∫ sec(x) dx = (1/2) ln |(1 + sin(x)) / (1 – sin(x))| + C.
Explanation: This method uses partial fraction decomposition to rewrite sec(x) as a sum of simpler fractions and then integrates each term individually to obtain the final result.
Using trigonometric formulas:
∫ sec(x) dx = ln |tan[(x/2) + (π/4)]| + C.
Explanation: This method employs trigonometric identities and half-angle formulas to transform the integral into a more manageable form and then integrates to find the solution.
Understanding these different methods provides valuable tools for evaluating the integral of sec(x) in various scenarios and helps deepen the understanding of integration techniques. Each method has its advantages and may be more convenient in specific situations.
Integration other trigonometric ratios
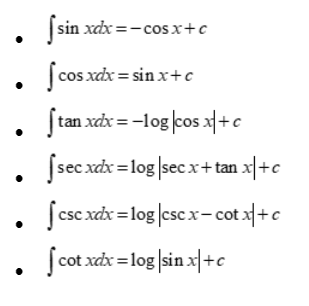
FAQs on Integration of Sec x
What is the formula for integral of sec(x)
The formula for the integral of sec(x) is: ∫ sec(x) dx = ln |sec(x) + tan(x)| + C, where C is the constant of integration. This formula can be obtained using different methods such as substitution, trigonometric formulas, or hyperbolic functions, as mentioned in the previous discussions. The integral of sec(x) is a common integral in calculus and frequently appears in various mathematical and scientific applications.
What is the trigonometric identity related to sec(x)
The trigonometric identity related to sec(x) is: sec^2(x) = 1 + tan^2(x). This identity is derived from the Pythagorean identity for right triangles, which states that for any right triangle with angle x, the square of the length of the hypotenuse (sec(x)) is equal to the sum of the squares of the lengths of the other two sides (1 for the adjacent side and tan(x) for the opposite side). Another way to write this identity is: 1 + tan^2(x) = sec^2(x). It is an essential trigonometric identity and is often used in trigonometric calculations and proofs.
How do you integrate sec(x)
Rewrite sec(x) as 1/cos(x). Multiply and divide the integrand by cos(x). Use the trigonometric identity cos^2(x) = 1 - sin^2(x). Substitute sin(x) = u and cos(x) dx = du. Decompose 1/(1 - u^2) using partial fractions. Integrate the result: (1/2) ln |(1 + sin(x))/(1 - sin(x))| + C.
What is the integral of sec(2x)
The integral of sec(2x) is: ∫sec(2x) dx = (1/2) ln |sec(2x) + tan(2x)| + C, where C is the constant of integration.
What is the derivative of tan(x)
The derivative of tan(x) is:d/dx (tan(x)) = sec^2(x).








