The Triangles and its Properties Class 7 Extra Questions Very Short Answer Type
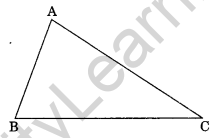
Question 1. In ∆ABC, write the following:
(a) Angle opposite to side BC.
(b) The side opposite to ∠ABC.
(c) Vertex opposite to side AC.
Solution:
(a) In ∆ABC, Angle opposite to BC is ∠BAC
(b) Side opposite to ∠ABC is AC
(c) Vertex opposite to side AC is B
Also Check: CBSE Syllabus for Class 1 to 12
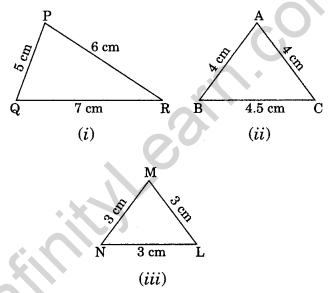
Question 2. Classify the following triangle on the bases of sides
Solution:
(i) PQ = 5 cm, PR = 6 cm and QR = 7 cm
PQ ≠ PR ≠ QR
Thus, ∆PQR is a scalene triangle.
(ii) AB = 4 cm, AC = 4 cm
AB = AC
Thus, ∆ABC is an isosceles triangle.
(iii) MN = 3 cm, ML = 3 cm and NL = 3 cm
MN = ML = NL
Thus, ∆MNL is an equilateral triangle.
Question 3.
In the given figure, name the median and the altitude. Here E is the midpoint of BC.
Solution
In ∆ABC, we have
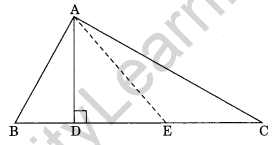
AD is the altitude.
AE is the median.
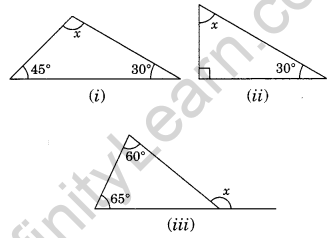
Question 4. In the given diagrams, find the value of x in each case.
Solution:
(i) x + 45° + 30° = 180° (Angle sum property of a triangle)
⇒ x + 75° – 180°
⇒ x = 180° – 75°
x = 105°
(ii) Here, the given triangle is right angled triangle.
x + 30° = 90°
⇒ x = 90° – 30° = 60°
(iii) x = 60° + 65° (Exterior angle of a triangle is equal to the sum of interior opposite angles)
⇒ x = 125°
Question 5.Which of the following cannot be the sides of a triangle?
(i) 4.5 cm, 3.5 cm, 6.4 cm
(ii) 2.5 cm, 3.5 cm, 6.0 cm
(iii) 2.5 cm, 4.2 cm, 8 cm
Solution:
(i) Given sides are, 4.5 cm, 3.5 cm, 6.4 cm
Sum of any two sides = 4.5 cm + 3.5 cm = 8 cm
Since 8 cm > 6.4 cm (Triangle inequality)
The given sides form a triangle.
(ii) Given sides are 2.5 cm, 3.5 cm, 6.0 cm
Sum of any two sides = 2.5 cm + 3.5 cm = 6.0 cm
Since 6.0 cm = 6.0 cm
The given sides do not form a triangle.
(iii) 2.5 cm, 4.2 cm, 8 cm
Sum of any two sides = 2.5 cm + 4.2 cm = 6.7 cm
Since 6.7 cm < 8 cm
The given sides do not form a triangle.
Question 6. In the given figure, find x.
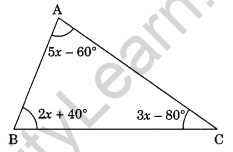
Solution:
In ∆ABC, we have
5x – 60° + 2x + 40° + 3x – 80° = 180° (Angle sum property of a triangle)
⇒ 5x + 2x + 3x – 60° + 40° – 80° = 180°
⇒ 10x – 100° = 180°
⇒ 10x = 180° + 100°
⇒ 10x = 280°
⇒ x = 28°
Thus, x = 28°
Question 7. One of the equal angles of an isosceles triangle is 50°. Find all the angles of this triangle.
Solution:
Let the third angle be x°.
x + 50° + 50° = 180°
⇒ x° + 100° = 180°
⇒ x° = 180° – 100° = 80°
Thus ∠x = 80°
Question 8.
In ΔABC, AC = BC and ∠C = 110°. Find ∠A and ∠B.
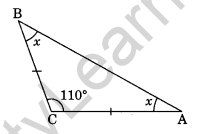
Solution:
In given ΔABC, ∠C = 110°
Let ∠A = ∠B = x° (Angle opposite to equal sides of a triangle are equal)
x + x + 110° = 180°
⇒ 2x + 110° = 180°
⇒ 2x = 180° – 110°
⇒ 2x = 70°
⇒ x = 35°
Thus, ∠A = ∠B = 35°
The Triangles and its Properties Class 7 Extra Questions Short Answer Type
Question 9. Two sides of a triangle are 4 cm and 7 cm. What can be the length of its third side to make the triangle possible?
Solution:
Let the length of the third side be x cm.
Condition I: Sum of two sides > the third side
i.e. 4 + 7 > x ⇒ 11 > x ⇒ x < 11
Condition II: The difference of two sides less than the third side.
i.e. 7 – 4 < x ⇒ 3 < x ⇒ x > 3
Hence the possible value of x are 3 < x < 11
i.e. x < 3 < 11
Question 10. Find whether the following triplets are Pythagorean or not?
(a) (5, 8, 17)
(b) (8, 15, 17)
Solution: (a) Given triplet: (5, 8, 17)
172 = 289
82 = 64
52 = 25
82 + 52 = 64 + 25 = 89
Since 89 ≠ 289
52 + 82 ≠ 172
Hence (5, 8, 17) is not Pythagorean triplet.
(b) Given triplet: (8, 15, 17)
172 = 289
152 = 225
82 = 64
152 + 82 = 225 + 64 = 289
172 = 152 + 82
Hence (8, 15, 17) is a Pythagorean triplet.
Question 11. In the given right-angled triangle ABC, ∠B = 90°. Find the value of x.
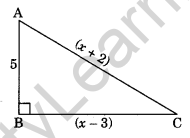
Solution: In ΔABC, ∠B = 90°
AB2 + BC2 = AC2 (By Pythagoras property)
(5)2 + (x – 3)2 = (x + 2)2
⇒ 25 + x2 + 9 – 6x = x2 + 4 + 4x
⇒ -6x – 4x = 4 – 9 – 25
⇒ -10x = -30
⇒ x = 3
Hence, the required value of x = 3
Question 12. AD is the median of a ΔABC, prove that AB + BC + CA > 2AD (HOTS)
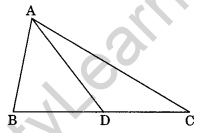
Solution: In ΔABD,
AB + BD > AD …(i)
(Sum of two sides of a triangle is greater than the third side)
Similarly, In ΔADC, we have
AC + DC > AD …(ii)
Adding (i) and (ii), we have
AB + BD + AC + DC > 2AD
⇒ AB + (BD + DC) + AC > 2AD
⇒ AB + BC + AC > 2AD
Hence, proved.
Question 13. The length of the diagonals of a rhombus is 42 cm and 40 cm. Find the perimeter of the rhombus.
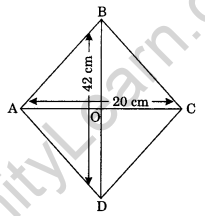
Solution: AC and BD are the diagonals of a rhombus ABCD.
Since the diagonals of a rhombus bisect at the right angle.
AC = 40 cm
AO = \(\frac { 40 }{ 2 }\) = 20 cm
BD = 42 cm
OB = \(\frac { 42 }{ 2 }\) = 21 cm
In right angled triangle AOB, we have
AO2 + OB2 = AB2
⇒ 202 + 212 = AB2
⇒ 400 + 441 = AB2
⇒ 841 = AB2
⇒ AB = √841 = 29 cm.
Perimeter of the rhombus = 4 × side = 4 × 29 = 116 cm
Hence, the required perimeter = 116 cm
Question 14. The sides of a triangle are in the ratio 3 : 4 : 5. State whether the triangle is right-angled or not.
Solution:
Let the sides of the given triangle are 3x, 4x and 5x units.
For right angled triangle, we have
Square of the longer side = Sum of the square of the other two sides
(5x)2 = (3x)2 + (4x)2
⇒ 25x2 = 9x2 + 16x2
⇒ 25x2 = 25x2
Hence, the given triangle is a right-angled.
Question 15. A plane flies 320 km due west and then 240 km due north. Find the shortest distance covered by the plane to reach its original position.
Solution:
Here, OA = 320 km
AB = 240 km
OB = ?
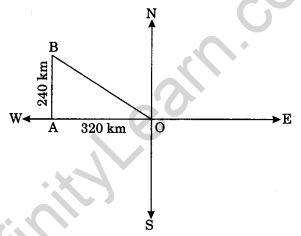
Clearly, ∆OBA is right angled triangle
OB2 = OA2 + AB2 (By Pythagoras property)
⇒ OB2 = 3202 + 2402
⇒ OB2 = 102400 + 57600
⇒ OB2 = 160000
⇒ OB = √160000 = 400 km.
Hence the required shortest distance = 400 km.
The Triangles and its Properties Class 7 Extra Questions Higher Order Thinking Skills (HOTS) Type
Question 16. In the following figure, find the unknown angles a and b, if l || m.
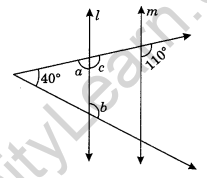
Solution:
Here, l || m
∠c = 110° (Corresponding angles)
∠c + ∠a = 180° (Linear pair)
⇒ 110° + ∠a = 180°
⇒ ∠a = 180° – 110° = 70°
Now ∠b = 40° + ∠a (Exterior angle of a triangle)
⇒ ∠b = 40° + 70° = 110°
Hence, the values of unknown angles are a = 70° and b = 110°
Question 17. In figure (i) and (ii), Find the values of a, b and c.
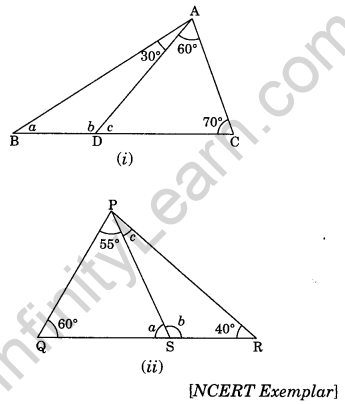
Solution:
(i) In ∆ADC, we have
∠c + 60° + 70° = 180° (Angle sum property)
⇒ ∠c + 130° = 180°
⇒ ∠c = 180° – 130° = 50°
∠c + ∠b = 180° (Linear pair)
⇒ 50° + ∠b = 180°
⇒ ∠ b = 180° – 50° = 130°
In ∆ABD, we have
∠a + ∠b + 30° = 180° (Angle sum property)
⇒ ∠a + ∠130° + 30° = 180°
⇒ ∠a + 160° = 180°
⇒ ∠a = 180° – 160° = 20°
Hence, the required values are a = 20°, b = 130° and c = 50°
(ii) In ∆PQS, we have
∠a + 60° + 55° = 180°(Angle sum property)
⇒ ∠a + 115° = 180°
⇒ ∠a = 180° – 115°
⇒ ∠a = 65°
∠a + ∠b = 180° (Linear pair)
⇒ 65° + ∠b = 180°
⇒ ∠b = 180° – 65° = 115°
In ∆PSR, we have
∠b + ∠c + 40° = 180° (Angle sum property)
⇒ 115° + ∠c + 40° = 180°
⇒ ∠c + 155° = 180°
⇒ ∠c = 180° – 155° = 25°
Hence, the required angles are a = 65°, b = 115° and c = 25°
Question 18. I have three sides. One of my angle measure 15°. Another has a measure of 60°. What kind of a polygon am I? If I am a triangle, then what kind of triangle am I? [NCERT Exemplar]
Solution:
Since I have three sides.
It is a triangle i.e. three-sided polygon.
Two angles are 15° and 60°.
Third angle = 180° – (15° + 60°)
= 180° – 75° (Angle sum property)
= 105°
which is greater than 90°.
Hence, it is an obtuse triangle.






