Distance Formula

What is distance formula?

The distance formula is a mathematical formula used to calculate the distance between two points in a coordinate plane

It is derived from the Pythagorean Theorem and is applicable in two- or three-dimensional space.

The formula allows us to find the straight-line distance between two points, regardless of the direction or path taken.

In a two-dimensional coordinate plane, the distance formula is given by:

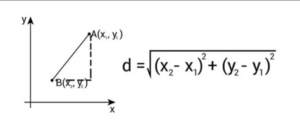
Distance:

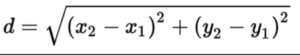
In this formula, (x1, y1) represents the coordinates of the first point, and (x2, y2) represents the coordinates of the second point. By subtracting the x-coordinates and y-coordinates of the two points, squaring them, adding the results, and taking the square root of the sum, we can determine the distance between the two points.

In a three-dimensional coordinate space, the distance formula is similar but includes an additional term for the z-coordinate:

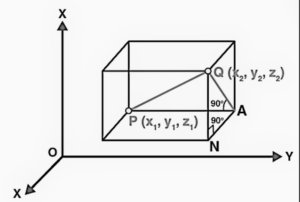
Distance formula:

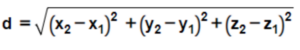
Here, (x1, y1, z1) represents the coordinates of the first point, and (x2, y2, z2) represents the coordinates of the second point. The formula calculates the straight-line distance in three dimensions.

To use the distance formula, simply substitute the coordinates of the two points into the formula and perform the necessary calculations. The resulting value represents the distance between the two points.

The distance formula is widely used in various fields, including mathematics, physics, engineering, and computer science. It provides a fundamental tool for measuring distances and determining spatial relationships between points.

Solved examples on Distance Formula:

Example 1: Find the distance between the points A(2, 3) and B(5, 1).

Solution:

Using the distance formula:

Distance:

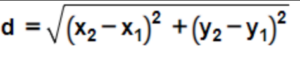
Substituting the given coordinates:

Distance = √((5 – 2)² + (1 – 3)²)

Distance = √(3² + (-2)²)

Distance = √(9 + 4)

Distance = √13

Distance ≈ 3.61

Therefore, the distance between points A(2, 3) and B(5, 1) is approximately 3.61 units.

Example 2: Determine the distance between the points P(-1, 2) and Q(4, -3).

Solution:

Using the distance formula:

Distance:

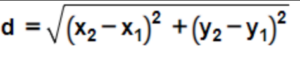
Substituting the given coordinates:

Distance = √((4 – (-1))² + (-3 – 2)²)

Distance = √((4 + 1)² + (-3 – 2)²)

Distance = √(5² + (-5)²)

Distance = √(25 + 25)

Distance = √50

Distance ≈ 7.07

Therefore, the distance between points P(-1, 2) and Q(4, -3) is approximately 7.07 units.

Example 3: Find the distance between the points R(0, 0) and S(0, 5).

Solution:

Using the distance formula:

Distance:

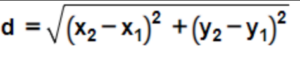
Substituting the given coordinates:

Distance = √((0 – 0)² + (5 – 0)²)

Distance = √(0² + 5²)

Distance = √25

Distance = 5

Therefore, the distance between points R(0, 0) and S(0, 5) is 5 units.

Frequently Asked Questions on Distance Formula

What is the distance formula?

The distance formula is a mathematical formula used to calculate the distance between two points in a coordinate plane. It is derived from the Pythagorean theorem and is represented as follows: Distance = √((x2 - x1)² + (y2 - y1)²), where (x1, y1) and (x2, y2) are the coordinates of the two points.

When is the distance formula used?

The distance formula is used when you want to find the straight-line distance between two points in a coordinate plane. It is applicable in various fields, including mathematics, physics, engineering, and computer science.

Can the distance formula be used in three dimensions?

Yes, the distance formula can be extended to three dimensions. In three-dimensional space, the formula is given as Distance = √((x2 - x1)² + (y2 - y1)² + (z2 - z1)²), where (x1, y1, z1) and (x2, y2, z2) are the coordinates of the two points.

Is the distance always positive?

Yes, the distance between two points is always positive or zero. It represents a physical distance, which cannot be negative.

Can the distance formula be used for non-integer coordinates?

Yes, the distance formula can be used for any real-valued coordinates, including non-integer coordinates. It provides an accurate measure of distance regardless of the coordinate values.

How is the distance formula derived?

The distance formula is derived from the Pythagorean Theorem. By considering the coordinates of two points as the lengths of the sides of a right triangle, the formula calculates the length of the hypotenuse, which represents the distance between the points.

Can the distance formula be applied to calculate the distance between more than two points?

No, the distance formula is specifically designed to find the distance between two points. To calculate the distance between multiple points, you would need to apply the formula iteratively for each pair of points.