Table of Contents
Introduction:
Equivalent resistance formulas are used in electrical circuits to simplify complex circuits into a single equivalent resistance. The equivalent resistance represents the total resistance that a current would encounter if it flowed through the entire circuit. Here are some important formulas related to equivalent resistance:
Equivalent Resistance Formula for Resistors in series:
Consider a simple circuit with three resistors R1, R2, and R3 connected in series along with an Ammeter and a plug key.
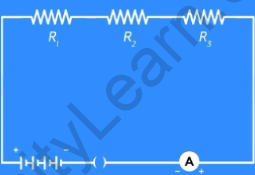
Resistors in series
Close the plug key and note down the Ammeter reading. Next, place the ammeter between the resistors R1 and R2, and then between R2 and R3 and note down the respective ammeter readings.
From the readings recorded, we see that the current is the same in each reading. Let this current be ‘I’ ampere. So, in a series of combinations of resistors, the current flowing is the same throughout the circuit.
Now remove the ammeter and insert a voltmeter across the start of the first resistor and the end of the third resistor. Then plug the key and note the potential difference across the resistors. Let’s say it’s ‘V’ volts.
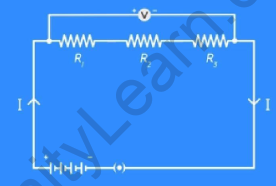
Disconnect the voltmeter and insert three voltmeters in the circuit, one across each of the resistors. Then plug the key and measure the potential difference across each of the resistors. You will notice that the potential difference across each of the resistors is different. Let’s call them V1, V2, and V3 respectively.
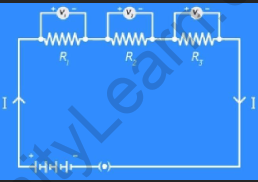
Even though the voltages are different, you will notice that the potential difference V is equal to the sum of the potential differences V1, V2, and V3.
V = V1 + V2 + V3 … (1)
Let the 3 resistors together form resistance of R ohms. Thus by Ohm’s Law,
V = IR … (2)
Similarly, applying Ohm’s law for each resistor,
V1 = IR1 … (3)
V2 = IR2 … (4)
V3 = IR3 … (5)
Now on substituting equations (2), (3), (4), and (5) in equation (1), IR = IR1 + IR2 + IR3
∴ Rs = R1 + R2 + R3
Thus, when two or more resistors are connected in series, then the overall combined resistance, denoted by ‘Rs’, is the sum of the individual resistances.
Equivalent Resistance Formula for Resistors in Parallel:
Consider a simple circuit with three resistors R1, R2 and R3, an Ammeter and a plug key. In this circuit, we have 3 resistors of different values connected in parallel since all the resistors have common start and endpoints. Let the points be X and Y.
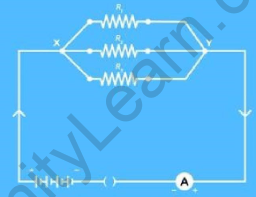
Resistors in parallel
The potential difference is always measured between two points. If the two points are common, it means the potential difference across each of the resistors will be the same.
The points X and Y are common for each of the resistors and also for the battery. So, if the potential difference across the battery is ‘V’ volts, then the potential difference across each resistor will also be V volts.
In this circuit, the current across each resistor will not be the same.
Let the current across R1, R2, and R3 be I1, I2, and I3 respectively. Let the total current flowing in the circuit be I. Then the total current I will be equal to the sum of the separate currents flowing through each of the resistors.
By Ohm’s Law,
I = V/Rp … (2)
Where Rp is the combined resistance of the resistors in parallel.
| Also, | |
| I1 = V/R1… | (3) |
| I2 = V/R2… | (4) |
| I3 = V/R3… | (5) |
The potential difference across each resistor will be the same as that of the battery. Substituting equations (2), (3), (4), and (5) in (1),
V/Rp = V/R1 + V/R2 + V/R3
∴ 1/Rp= 1/R1 + 1/R2 + 1/R3
Thus, when resistors are connected in parallel, the reciprocal of the equivalent resistance Rp is equal to the sum of the reciprocals of the individual resistances.
Solved Examples on Equivalent Resistance Formula:
Example 1: As shown in the figure, two resistors with resistances 10 Ω and 15 Ω are connected to a 5 V battery. Find the:
- Total resistance of the circuit
- Potential difference across the 15 Ohms resistor
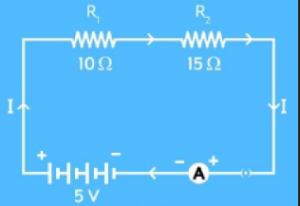
Figure 1
Given:
Resistance (R1) = 10 Ω Resistance (R2) = 15 Ω Potential difference (V) = 5 V
To find:
- Total resistance of the circuit (Rs)
- Potential difference across the 15 Ohms resistor (V2)
Formula:
- Rs = R1 + R2
- V2 = IR2
Solution:
From the circuit diagram, the two resistors are connected in series. ∴ Total Resistance of the circuit is given by
Rs = R1 + R2
∴ Rs = 10 + 15 = 25 Ω
∴ Rs = 25 Ω
Therefore, the total resistance of the circuit is 25 Ω .
Applying Ohm’s law to the entire circuit,
V = IRs
∴ 5 = I ✕ 25
∴ I = 5/25
∴ I = 0.2 A
When resistors are connected in series, the current flowing in the circuit will be the same at every point in the circuit.
Therefore, by using Ohm’s law, V2 = IR2
∴ V2 = 0.2 x 15 = 3V
Therefore, the potential difference across the 15 Ohms resistor is 3V.
Example 2: Consider a circuit with three resistors connected in series: R1 = 10 ohms, R2 = 20 ohms, and R3 = 30 ohms. Calculate the equivalent resistance of the circuit.
Solution: To find the equivalent resistance of resistors in series, we simply add up their individual resistances.
R_eq = R1 + R2 + R3
R_eq = 10 + 20 + 30
R_eq = 60 ohms
Therefore, the equivalent resistance of the circuit is 60 ohms.
Frequently Asked Questions on Equivalent Resistance Formula:
1: How do you find the equivalent resistance of parallel?
Answer: To find the equivalent resistance of resistors connected in parallel, use the formula:
1/Req = 1/R1 + 1/R2 + 1/R3 + …
where Req is the equivalent resistance and R1, R2, R3, … are the individual resistances in parallel. In other words, calculate the reciprocal of each resistance, sum them up, and take the reciprocal of the sum to obtain the equivalent resistance.
2: Why is equivalent resistance less in parallel?
Answer: In a parallel connection of resistors, the current divides among the branches, resulting in a lower equivalent resistance compared to a series connection. Each resistor in parallel has the same voltage across it, but the current is divided based on the resistances. According to Ohm’s Law, lower resistance allows for a larger current to flow. In a parallel circuit, the branches with lower resistance offer less opposition, allowing more current to flow through them. This combined effect of multiple paths for current flow leads to a lower total resistance in a parallel connection.
3: What is equivalent resistance?
Answer: The equivalent resistance is the combined resistance of multiple resistors in a circuit. It represents a single resistor that would have the same effect on current flow as the combination of all the individual resistors. The equivalent resistance can be found by summing the resistances in series or using the reciprocal of the sum of reciprocals in parallel.
4: What is the equivalent resistance formula of series and parallel?
Answer: The formula for calculating the equivalent resistance in a series connection is obtained by summing the individual resistances: Rs = R1 + R2 + R3 + … In a parallel connection, the formula involves taking the reciprocal of the sum of the reciprocals of the individual resistances: Rp = (1/R1 + 1/R2 + 1/R3 + …)-1.
5: What is the equivalent resistance formula for 2 resistors in parallel?
Answer: The formula for calculating the equivalent resistance of two resistors in parallel is given by: Rp = (R1 x R2) / (R1 + R2). This formula takes into account the reciprocals of the resistances and their sum to determine the overall resistance of the parallel combination of resistors.
6: What is the total resistance for two 2-ohm resistors connected in parallel?
Answer: When two 2-ohm resistors are connected in parallel, the total resistance can be calculated using the formula Rp = (R1 x R2) / (R1 + R2). Substituting the values, we get Rp = (2 x 2) / (2 + 2) = 4/4 = 1 ohm. Therefore, the total resistance for two 2-ohm resistors connected in parallel is 1 ohm.
7: What is the best way to find equivalent resistance?
Answer: The best way to find the equivalent resistance in a circuit depends on the specific circuit configuration.
If the circuit consists of resistors connected in series and parallel, the best approach is to simplify the circuit step-by-step. Start by identifying resistors that are in series and calculate their equivalent resistance using the series formula (R_eq = R1 + R2 + …). Then, identify resistors in parallel and calculate their equivalent resistance using the parallel formula (1/R_eq = 1/R1 + 1/R2 + …). Repeat this process until you have simplified the entire circuit into a single equivalent resistance.
8: Which kind of connection will have higher equivalent resistance?
Answer: In a series connection of resistors, the equivalent resistance is obtained by summing the individual resistances, resulting in a higher overall resistance than a parallel connection. In series, the same current flows through each resistor, while in parallel, the voltage across each resistor is the same. The reciprocal of the sum of the reciprocals of the individual resistances gives the equivalent resistance in parallel, which is always smaller than the smallest individual resistance. Thus, a series connection yields a higher equivalent resistance compared to a parallel connection when using the same set of resistors.
9: What is the unit of equivalent resistance?
Answer: The unit of equivalent resistance is the same as the unit of resistance, which is the ohm (Ω). The ohm is the standard unit of electrical resistance in the International System of Units (SI).
The ohm is represented by the symbol Ω and is named after the German physicist Georg Simon Ohm. It is defined as the resistance between two points in a conductor when a constant current of one ampere (A) is flowing through it, producing a potential difference of one volt (V) across the conductor.
Therefore, when calculating the equivalent resistance of a circuit, the resulting value will be expressed in ohms (Ω). This unit indicates the level of opposition to the flow of electric current offered by the circuit or component.
10: Is equivalent resistance the same as individual resistance?
Answer: No, the equivalent resistance is not the same as the individual resistance of a single resistor in a circuit. The equivalent resistance refers to the single resistance value that would replace a combination of resistors in a circuit while maintaining the same overall effect on current flow.
When resistors are connected in different configurations (such as series or parallel), their individual resistances combine to create an overall effect on the circuit. The equivalent resistance represents this combined effect and simplifies the circuit analysis by reducing multiple resistors to a single equivalent resistor.



