Parallelogram Formula

Introduction

A parallelogram is a special kind of quadrilateral. If a quadrilateral has two pairs of parallel opposite sides, then it is called a parallelogram. Finding the area of parallelograms has very important applications in real life such as agriculture, construction, physics, etc.

What is the perimeter of a parallelogram?

A parallelogram is a quadrilateral which has its opposite sides parallel and equal in length. The perimeter of the parallelogram is twice the sum of one pair of its adjacent sides.

Consider a parallelogram whose adjacent sides are of length ‘a’ and ‘b’.

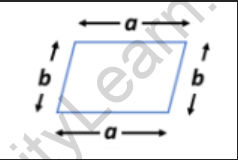
Thus, the perimeter of the parallelogram = a + b + a + b

= 2a + 2b

= 2(a + b)

Alternatively, we can also use the formula:

Perimeter = 2(l + w)

In this formula, ‘l’ represents the length of the parallelogram, and ‘w’ represents its width.

It’s important to note that the perimeter of a parallelogram is always expressed in the same unit as the lengths of the sides.

The perimeter formula allows us to quickly determine the total length of the sides of a parallelogram, which is useful in various applications, such as calculating fencing requirements, estimating material quantities, or determining the distance around a given shape.

What is the area of a parallelogram?

The formula for the area of a parallelogram is a fundamental concept in geometry. The area (A) of a parallelogram is determined by multiplying the length of its base (b) by its corresponding height (h).
The area (A) of a parallelogram is given by the formula: A = base × height.

The base refers to any one of the parallel sides of the parallelogram, and the height represents the perpendicular distance between the base and its opposite side. The formula highlights the relationship between the base and height in determining the amount of space enclosed within the parallelogram. It is a simple yet powerful formula that applies to all parallelograms, regardless of their size or orientation.

Solved Examples on Parallelogram Formula:

Example 1: Find the area of a parallelogram with a base of 8 cm and a height of 5 cm.

Solution:

Using the formula for the area of a parallelogram, we have:

Area = base × height

Area = 8 cm × 5 cm

Area = 40 cm²

Therefore, the area of the parallelogram is 40 cm².

Example 2: The perimeter of a parallelogram is 30 meters, and one side is 8 meters long. Find the length of the adjacent side.

Solution:

Let the length of the adjacent side be x.

Given that the perimeter is 30 meters, we can write the equation:

Perimeter = 2 × (length of base + length of adjacent side)

30 = 2 × (8 + x)

Simplifying the equation:

30 = 16 + 2x

2x = 30 – 16

2x = 14

x = 7

Therefore, the length of the adjacent side is 7 meters.

Frequently Asked Questions on Parallelogram Formula:

1: What is the rule for the perimeter of a parallelogram?

Answer: The rule for calculating the perimeter of a parallelogram is to add the lengths of all four sides. Since opposite sides of a parallelogram are equal in length, the formula for the perimeter simplifies to P = 2a + 2b, where ‘a’ and ‘b’ represent the lengths of two adjacent sides. Alternatively, we can use the formula P = 2(l + w), where ‘l’ is the length and ‘w’ is the width of the parallelogram. By adding the lengths of the sides, we can determine the total distance around the parallelogram, which gives us its perimeter.

2: Do all parallelograms with the same perimeter have the same area?

Answer: No, not all parallelograms with the same perimeter have the same area. The area of a parallelogram depends not only on its perimeter but also on the dimensions of its sides and the angle between those sides. Parallelograms with different side lengths and angles can have the same perimeter but different areas.
For example, consider two parallelograms with the same perimeter: one could have longer sides and acute angles, while the other could have shorter sides and obtuse angles. Despite having the same perimeter, the first parallelogram will generally have a larger area than the second parallelogram.

3: What are the properties of a parallelogram ?

Answer: The seven properties of a parallelogram are as follows:

Opposite sides are parallel: The opposite sides of a parallelogram are always parallel, meaning they will never intersect.

Opposite sides are equal in length: The opposite sides of a parallelogram are of equal length. This property makes the opposite sides congruent.

Opposite angles are equal: The opposite angles of a parallelogram are congruent. In other words, they have the same measure.

Consecutive angles are supplementary: The consecutive angles of a parallelogram add up to 180 degrees. In other words, they are supplementary.

Diagonals bisect each other: The diagonals of a parallelogram bisect each other, meaning they divide each other into two equal halves.

Diagonals create congruent triangles: The diagonals of a parallelogram create congruent triangles with the sides of the parallelogram.

Opposite sides and angles are congruent: The opposite sides and angles of a parallelogram are congruent to each other.

These properties are unique to parallelograms and can be used to identify and classify shapes based on their characteristics.

4: What is the formula for the area of a parallelogram?

Answer: The formula for the area of a parallelogram is A = base × height, where the base represents the length of one of the parallel sides and the height represents the perpendicular distance between the base and its opposite side.

5: Can you find the area of a parallelogram with only the lengths of the sides?

Answer: No, you cannot find the area of a parallelogram with only the lengths of the sides. The area calculation requires the measurement of the base and the corresponding height.

6: What is the Area of a Parallelogram Formula?

Answer: The area of a parallelogram can be calculated by finding the product of its base with the altitude. The base and altitude of a parallelogram are always perpendicular to each other. The formula to calculate the area of a parallelogram is given as Area of parallelogram = (base × height) square units.

7: How to Find Area of a Parallelogram Without Height?

Answer: The area of a parallelogram can be calculated without the height when the length of adjacent sides and the angle between them is known. The formula to find the area for this case is given as, area = ab sin (θ), where ‘a’ and ‘b’ are lengths of adjacent sides, and, θ is the angle between them.

Also, the area can be calculated when the diagonals and their intersecting angle are given, using the formula, Area = ½ × d1 × d2 sin (y), where ‘d1’ and ‘d2’ are lengths of diagonals of the parallelogram, and ‘y’ is the angle between them.

8: How to Calculate the Area of Parallelogram Whose Adjacent Sides are Given?

Answer: To find the area of a parallelogram when the lengths of adjacent sides are given, we need the angle between them. The formula to find the area for this case is given as, area = ab sin (θ), where ‘a’ and ‘b’ are lengths of adjacent sides, and, θ is the angle between the adjacent sides of the parallelogram.