Table of Contents
Introduction
The radius (denoted by “r”) is a crucial measurement in geometry, particularly when dealing with circles and spheres. While the radius has its own formulas, it can also be expressed in terms of other measurements. Here are some notes on finding the radius formula in terms of diameter, area, surface area, volume, and other related quantities:
Definition and Formula
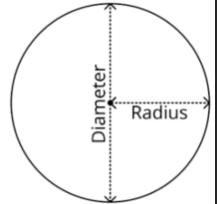
Diameter: The diameter (denoted by “d”) is the length of a line segment that passes through the center of a circle or sphere, connecting two points on its circumference or surface, respectively. The relationship between radius and diameter is:
Diameter(d) = 2r
Solving for the radius gives:
r = d/2
Area of a Circle: The area of a circle (denoted by “A”) can be used to find the radius by rearranging the area formula:
Area = πr2
Solving for the radius gives:
r = √(Area/π)
Circumference of a Circle: The circumference of a circle (denoted by “C”) can also be used to find the radius by rearranging the circumference formula:
Circumference = 2πr
Solving for the radius gives:
r = Circumference / (2π)
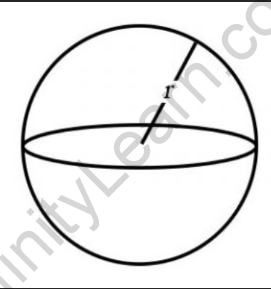
Surface Area of a Sphere: The surface area of a sphere (denoted by “SA”) can be used to find the radius by rearranging the surface area formula:
Surface Area = 4πr2
Solving for the radius gives:
r = √(Surface Area / (4π))
Volume of a Sphere: The volume of a sphere (denoted by “V”) can be used to find the radius by rearranging the volume formula:
Volume = (4/3)πr3
Solving for the radius gives:
r = ∛(Volume / ((4/3)π))
Understanding how to express the radius formula in terms of other measurements allows for flexibility in solving geometry problems and relating different geometric quantities. These formulas enable the calculation of the radius based on given information or the derivation of the radius when other quantities are known.
Solved Examples on Radius Formula:
Example 1: Finding Radius from Diameter
Given: Diameter = 12 cm
To find: Radius (r)
Solution:
Using the relationship between radius and diameter: Diameter = 2r
Substituting the given value: 12 cm = 2r
Dividing both sides by 2: r = 6 cm
Therefore, the radius is 6 cm.
Example 2: Finding Radius from Area of a Circle
Given: Area = 154 sq. units
To find: Radius (r)
Solution:
Using the formula: Area = πr^2
Substituting the given value: 154 = πr^2
Dividing both sides by π and taking the square root: r = √(154/π) ≈ 7 units
Therefore, the radius is approximately 7 units.
Example 3: Finding Radius from Circumference of a Circle
Given: Circumference = 30 cm
To find: Radius (r)
Solution:
Using the formula: Circumference = 2πr
Substituting the given value: 30 = 2πr
Dividing both sides by 2π: r = 30 / (2π) ≈ 4.77 cm
Therefore, the radius is approximately 4.77 cm.
Example 4: Finding Radius from Surface Area of a Sphere
Given: Surface Area = 314 sq. units
To find: Radius (r)
Solution:
Using the formula: Surface Area = 4πr2
Substituting the given value: 314 = 4πr2
Dividing both sides by 4π and taking the square root: r = √(314 / (4π)) ≈ 3.55 units
Therefore, the radius is approximately 3.55 units.
Frequently asked questions on Radius Formula:
1: What is the basic formula for radius?
Answer: The basic formula for radius depends on the context. In the case of a circle, the radius (r) is the distance from the center of the circle to any point on its circumference. The basic formula to calculate the radius of a circle is: r = √(A / π), where A represents the area of the circle. In the case of a sphere, the radius (r) is the distance from the center to any point on its surface. The basic formula to calculate the radius of a sphere is: r = ∛(V / ((4/3) x π)), where V represents the volume of the sphere.
2: How is the radius related to the diameter?
Answer: The radius and diameter of a circle are related as follows:
The radius is half the length of the diameter.
Mathematically, we can express this relationship as: Radius = Diameter / 2
The diameter is twice the length of the radius.
Mathematically, we can express this relationship as: Diameter = 2 x Radius
In other words, if you know the value of the radius, you can find the diameter by multiplying the radius by 2. Conversely, if you know the value of the diameter, you can find the radius by dividing the diameter by 2. The radius and diameter are interrelated and provide different ways to measure the size of a circle.
3: How can I find the radius if I know the area of a circle?
Answer: If you know the area of a circle, you can find the radius by using the formula:
Radius = √(Area / π).
Here, π represents the mathematical constant pi.
4: What is the relation between the radius and circumference of a circle?
Answer: To find the radius from the circumference, you can use the formula:
Radius = Circumference / (2 x π).
5: What is the radius of a circle?
Answer: The radius of a circle is the distance from the center of the circle to any point on its circumference. It is denoted by the symbol “r.”
6: How is Diameter Related to the Radius of the Circle?
Answer: The diameter of a circle is twice the radius. It can also be said that the length of the radius is half the diameter. The relation between radius and diameter can be expressed in the formula: Diameter = 2 × radius. Use a free online radius calculator to calculate the radius with the given diameter.
7: How to Find the Radius from Circumference?
Answer: The circumference of a circle and radius are related to each other and their relation can be expressed as Circumference = 2πr, where ‘r’ is the radius. So, when the circumference is known, the formula used to calculate the radius of a circle is Radius = Circumference / 2π.
8: What is the Radius Formula?
Answer: The radius of a circle can be calculated through various formulas. Observe the following formulas to calculate the radius:
When the diameter is known, the formula is, Radius = Diameter / 2
When the circumference is known, the formula is, Radius = Circumference / 2π
When the area is known, the formula is, Radius = ⎷(Area of the circle / π)







