Table of Contents
Trapezoid Formula
Introduction
Trapezoids are quadrilaterals that have two parallel sides and two non-parallel sides. It is also called a Trapezium. A trapezoid is a four-sided closed shape or figure which cover some area and also has its perimeter. It is a 2D figure and not 3D figure. The sides which are parallel to each other are termed the bases of the trapezoid. The non-parallel sides are known as legs or lateral sides. The distance between the parallel sides is known as the altitude. The area of trapezium along with its types, properties and other trapezoid-related formulas are provided here in this article.
Trapezoid Formula
The trapezoid formula is used to calculate the area of a trapezoid, a quadrilateral with one pair of parallel sides. The formula states that the area (A) of a trapezoid is equal to half the sum of the lengths of its parallel sides (base1 and base2) multiplied by the height (h).
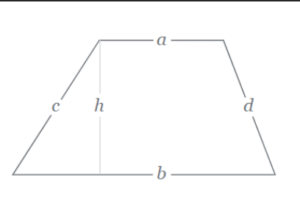
Mathematically, the formula can be written as:
A = (1/2) x (base1 + base2) x h
To understand how this formula is derived, we can break down the trapezoid into a rectangle and two triangles. The height of the trapezoid is the perpendicular distance between the parallel sides, and it determines how tall the trapezoid is.
The rectangle is formed by extending the shorter base (base1) to the longer base (base2). Its width is equal to the height of the trapezoid. Thus, the area of the rectangle is base1 x h.
Next, we have two triangles. Each triangle is formed by one of the bases and the height of the trapezoid. The area of a triangle is calculated as half the base multiplied by the height. Therefore, the combined area of both triangles is (1/2) x base2 x h.
Adding the area of the rectangle and the two triangles together, we get the total area of the trapezoid:
A = (base1 x h) + (1/2 x base2 x h) = (1/2) x (base1 + base2) x h
This formula allows us to calculate the area of a trapezoid by knowing the lengths of its parallel sides and the height. It is important to ensure that the bases are parallel for the formula to be valid.
Solved Examples on Trapezoid Formula:
Example 1: Find the area of a trapezoid with base1 = 5 cm, base2 = 9 cm, and height = 4 cm.
Solution:
Using the trapezoid formula: A = (1/2) x (base1 + base2) x height
Substituting the given values: A = (1/2) x (5 + 9) x 4
Calculating: A = (1/2) x 14 x 4
A = 28 cm2
Therefore, the area of the trapezoid is 28 square centimeters.
Example 2:
The area of a trapezoid is 45 square units. The length of base1 is 8 units, and the length of base2 is 12 units. Find the height.
Solution:
Using the trapezoid formula: A = (1/2) x (base1 + base2) x height
Substituting the given values: 45 = (1/2) x (8 + 12) x height
Simplifying: 45 = (1/2) x 20 x height
45 = 10 x height
Dividing both sides by 10: height = 4.5 units
Therefore, the height of the trapezoid is 4.5 units.
Example 3: The area of a trapezoid is 72 square inches. The length of base1 is 10 inches, and the height is 8 inches. Find the length of base2.
Solution:
Using the trapezoid formula: A = (1/2) x (base1 + base2) x height
Substituting the given values: 72 = (1/2) x (10 + base2) x 8
Simplifying: 72 = 4 x (10 + base2)
Dividing both sides by 4: 18 = 10 + base2
Subtracting 10 from both sides: base2 = 8 inches
Therefore, the length of base2 is 8 inches.
Frequently Asked Questions on Trapezoid Formula:
What is the formula for finding the area of a trapezoid?
The formula for finding the area of a trapezoid is (1/2) multiplied by the sum of the lengths of its parallel sides, known as the bases, multiplied by the height of the trapezoid. Mathematically, it can be expressed as Area = (1/2) x (base1 + base2) x height.
Are the diagonals of a trapezoid equal?
No, the diagonals of a trapezoid are not necessarily equal in length. A trapezoid is a quadrilateral with one pair of parallel sides. The diagonals of a trapezoid are the line segments connecting non-adjacent vertices. In a trapezoid, the diagonals are usually of different lengths, except in the special case of an isosceles trapezoid. In an isosceles trapezoid, the diagonals are equal, as the non-parallel sides are congruent. However, in a general trapezoid, the diagonals can have different lengths, depending on the specific dimensions and shape of the trapezoid.
Can a trapezoid be a square?
A trapezoid can be a square if all the sides are equal in length and at right angles to each other. So, all squares are trapezoids, but, not all trapezoids are squares.
Can a trapezoid have perpendicular diagonals?
Trapezoids do not necessarily have perpendicular diagonals. A trapezoid, however, can be drawn and oriented in such a way it has perpendicular diagonals.
Can the trapezoid formula be used if the bases are not parallel?
No, the trapezoid formula is only applicable when the trapezoid has one pair of parallel sides. If the bases are not parallel, a different formula or approach is required to calculate the area.
What are the different types of trapezoids?
There are different types of trapezoids: isosceles trapezoid, right trapezoid, and scalene trapezoid. A trapezoid with two non-parallel sides of the same length is called an isosceles trapezoid.
Is trapezoid a quadrilateral?
Yes, a trapezoid is a quadrilateral who has its two sides parallel and the other two sides are non-parallel.
What are the three attributes of trapezoids?
The base angles and the diagonals of an isosceles trapezoid are equal. The intersection point of the diagonals is collinear to the midpoints of the two opposite sides. Opposite sides of an isosceles trapezoid are of the same length or congruent to each other.







