Volume of Parallelepiped Formula 

Volume of Parallelepiped Formula

Introduction to Volume of Parallelepiped Formula

A parallelepiped is a three-dimensional shape that is formed by six parallelograms. The word ‘parallelepiped’ is derived from the Greek word parallelepipdon, meaning “a body having parallel bodies”. We can say that a parallelepiped relates with a parallelogram just like a cube relates with a square. Parallelepiped has 6 parallelogram-shaped faces, 8 vertices, and 12 edges. Let us understand properties and different formulas associated with a surface area and volume of a parallelepiped in the following sections.

What Is a Parallelepiped?

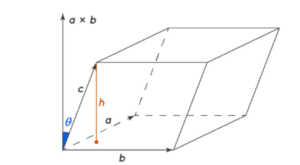
A parallelepiped is a three-dimensional shape with six faces, that are all in the shape of a parallelogram. It has 6 faces, 8 vertices, and 12 edges. Cube, cuboid, and rhomboid are all special cases of a parallelepiped. A cube is a parallelepiped whose all sides are square-shaped. Similarly, a cuboid and a rhomboid are parallelepipeds with rectangle and rhombus-shaped faces respectively. In the figure given below, we can observe a parallelepiped, with ‘a’, ‘b’, and ‘c’ as side lengths and ‘h’ as the height of the parallelepiped.

Properties of Parallelepiped

There are certain properties of a parallelepiped that help us distinguish it from other 3-D shapes. These properties are listed below,

• Parallelepiped is a three-dimensional solid shape.
• It has 6 faces, 12 edges, and 8 vertices.
• All faces of a parallelepiped are in the shape of a parallelogram.
• A parallelepiped has 2 diagonals on each face, called the face diagonals. It has a total of 12 face diagonals.
• The diagonals connecting the vertices not lying on the same face are called the body or space diagonal of a parallelepiped.
• Parallelepiped is referred to as a prism with a parallelogram-shaped base.
• Each face of a parallelepiped is a mirror image of the opposite face.

Volume of Parallelepiped

The volume of a parallelepiped is defined as the space occupied by the shape in a three-dimensional plane. The volume of a parallelepiped is expressed in cubic units, like in3, cm3, m3, ft3, yd3, etc.

Volume of Parallelepiped Formula

Volume of parallelepiped can be calculated using the base area and the height. The formula to calculate the volume of a parallelepiped is given as,

V = B × H

where,

B = Base area

H = Height of parallelepiped

Solved Examples on Volume of Parallelepiped Formula

Example 1: If the base face of a parallelepiped has opposite sides measuring 6 inches and 10 inches and its height is 7 inches, find the lateral surface area of the parallelepiped.

Solution:

Using the lateral area of parallelepiped formula,

LSA = Perimeter of base × height

⇒ LSA = 2(6 + 10) × 7 = 224 in2

Lateral area of given parallelepiped = 224 in2.

Example 2: A gift is packed in a rectangular box of dimensions 10 in, 7 in, and 8 in and it needs to be wrapped with gift paper. How much gift paper is required to wrap the gift box?

Solution:

The dimensions of the given gift box are,

length, l = 10 in

width, w = 7 in

height, h = 8 in

To find the amount of gift paper required, we need to find the total surface area of the box. Since the shape of the box can be compared to a rectangular parallelepiped,

TSA = 2 (lw + wh + hl)

= 2 (10 × 7 + 7 × 8 + 8 × 10)

= 2 (70 + 56 + 80)

= 412 in2.

The amount area of the gift paper required = 412 in2.

Frequently Asked Questions on Volume of Parallelepiped Formula

What Is Meant By a Parallelepiped?

Parallelepiped is a three-dimensional shape with 6 parallelogram-shaped faces, 12 edges, and 8 vertices. Parallelepiped is often referred to as a prism with a parallelogram-shaped base. Cube, cuboid, and rhomboid are all special cases of a parallelepiped with faces of the shape of a square, rectangle, and rhombus respectively.

What Is the Volume of a Parallelepiped?

The volume of a parallelepiped is the capacity or the shape or the total space occupied in a three-dimensional plane. The volume of the parallelepiped by cubic units, like in3, cm3, ft3, in3, etc.

What Is the Total Surface Area of a Parallelepiped?

The total surface area of a parallelepiped is the area covered by all the faces of a parallelepiped. It is expressed in square units, like in2, m2, cm2, ft2, etc.

What Is the Lateral Surface Area of a Parallelepiped?

The lateral surface area of a parallelepiped is the area or region covered by all the lateral or side faces of a parallelepiped. It is expressed in square units, using units like square inches, square meters, square feet, etc.

What Is a Rectangular Parallelepiped?

A rectangular parallelepiped is a type of parallelepiped whose all six faces are in a rectangular shape and the length of the parallel edges are equal.

What Is the Shape of a Parallelepiped?

Parallelopiped is a 3-D shape that has all the sides in the shape of a parallelogram. The opposite faces of a parallelepiped are mirror images of eachother.

How do you find the base area of a parallelepiped?

The three pairs of parallel faces form a hexahedron. For a given parallelepiped, let S is the area of the bottom face and H is the height, then the volume formula is given by; Since the base of parallelepiped is in the shape of a parallelogram, therefore we can use the formula for the area of the parallelogram to find the base area.

What Are the Parallelepiped Formulas?

Answer: The formulas associated with a parallelepiped are given as,

• LSA of parallelepiped = P × H
• TSA of parallelepiped = (P × H) + (2 × B)
• Volume of parallelepiped = B × H

where, B is the base area, H is the height of the parallelepiped, and P is the perimeter of base.