Table of Contents
Gravitational Acceleration Formula
Introduction:
Gravitational acceleration, often denoted as “g,” is a fundamental concept in physics that describes the acceleration experienced by objects due to the force of gravity. It is a measure of how quickly an object accelerates downward when dropped or falls freely under the influence of gravity. Gravitational acceleration is a universal constant near the Earth’s surface, approximately equal to 9.8 meters per second squared (9.8 m/s2). This acceleration determines the speed at which objects fall and plays a crucial role in understanding various phenomena, including projectile motion, free fall, and the behavior of celestial bodies.
Gravitational Acceleration Definition:
Gravitational acceleration is the acceleration experienced by an object due to the force of gravity. It represents the rate at which an object’s velocity changes when subjected to the gravitational pull of a massive body, such as a planet or a star.
Formula for Gravitational Acceleration:
The formula for gravitational acceleration, also known as acceleration due to gravity, relates the gravitational force acting on an object to its mass and the gravitational constant. The formula is as follows:
g = (G x M) / r2
where:
- “g” represents the gravitational acceleration.
- “G” is the gravitational constant, approximately equal to 6.67430 × 10-11 m3/(kg·s2).
- “M” represents the mass of the object that is causing the gravitational force.
- “r” represents the distance between the center of mass of the object causing the force and the center of mass of the object experiencing the force.
This formula describes how the gravitational force changes with distance and the masses of the objects involved. The gravitational acceleration is the acceleration experienced by an object in free fall near the surface of a massive body, such as Earth. On the surface of Earth, the gravitational acceleration is approximately 9.8 m/s2.
Derivation of Gravitational Acceleration Formula:
Let us try to find the value of acceleration due to gravity. For this, we will consider the case of a freely falling object. Consider a stone of mass ‘m’ falling freely under the influence of gravity only.
According, to Newton’s second law the force acting on the stone will be:
![]()
Now, if we consider the mass of the Earth to be ‘M’ and the distance between the stone of mass ‘m’ and the Earth to be ‘d’. As the distance between the center of the stone to the earth’s surface is negligible, we can consider ‘d’ as the radius ‘R’ of the earth. The gravitational force formula is given as,
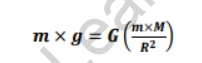
Dividing both sides by the mass of the object ‘m,’

The values of universal gravitational constant, the mass of the earth ‘M,’ and the radius of the earth ‘R’ are,
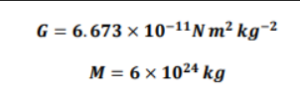
![]()
On substituting them, we get the value of acceleration due to the gravity on the earth as,
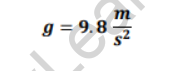
Also Read
Solved Examples on Gravitational Acceleration Formula:
Example 1: Determine the gravitational acceleration between two objects, one with a mass of 100 kg and the other with a mass of 50 kg, when they are 10 meters apart.
Solution:
Given:
Mass of object 1 (M1) = 100 kg
Mass of object 2 (M2) = 50 kg
Distance between the objects (r) = 10 meters
Using the formula g = G x (M1 + M2) / r2, we can calculate the gravitational acceleration:
g = (6.67430 × 10-11 x (100 kg + 50 kg) / (10 m)
g ≈ 1.12 × 10-9 m/s2
Therefore, the gravitational acceleration between the two objects is approximately 1.12 × 10-9 m/s2 .
Example 2: Calculating the acceleration due to gravity on the surface of a planet
Given:
Mass of the planet (M) = 5.972 × 1024 kg
Radius of the planet (r) = 6.371 × 106 meters
Gravitational constant (G) = 6.67430 × 10-11 N(m/kg)2
To determine the acceleration due to gravity (g) on the planet’s surface, we use the formula:
g = (G x M) / r2
Substituting the values:
g = (6.67430 × 10-11 x 5.972 × 1024 kg) / (6.371 × 106 m)2
g = (6.67430 × 10-11 x 5.972 × 1024 kg) / 4.049 × 1013 m2
g = 9.8227 m/s2
Therefore, the acceleration due to gravity on the surface of the planet is approximately 9.8227 m/s2.
Frequently Asked Questions on Gravitational Acceleration Formula:
1: What is the gravitational formula of acceleration?
Answer: The formula for gravitational acceleration is as follows:
g = G x M / r2
where:
- “g” represents the gravitational acceleration.
- “G” is the gravitational constant, approximately equal to 6.67430 × 10-11 m3/(kg·s2).
- “M” represents the mass of the object that is causing the gravitational force.
- “r” represents the distance between the center of mass of the object causing the force and the center of mass of the object experiencing the force.
2: Is gravitational acceleration zero?
Answer: No, gravitational acceleration is not zero. Gravitational acceleration exists whenever there is a gravitational force acting on an object. On Earth, the gravitational acceleration is approximately 9.8 m/s², causing objects to accelerate towards the Earth’s surface. However, the value of gravitational acceleration can vary depending on the mass and distance from other celestial bodies.
3: How do you calculate 9.8 m/s2?
Answer: Gravitational Acceleration Formula is given by:
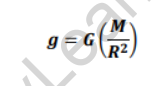
The values of universal gravitational constant, the mass of the earth ‘M,’ and the radius of the earth ‘R’ are,
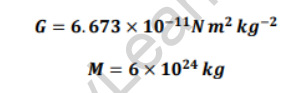
![]() On substituting them, we get the value of acceleration due to the gravity on the earth as,
On substituting them, we get the value of acceleration due to the gravity on the earth as,
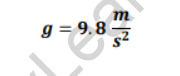
4: Is acceleration due to gravity(g) a universal constant?
Answer: Acceleration due to gravity (g) is not a universal constant. It varies depending on the location and the mass of the celestial body exerting the gravitational force. On Earth, the average value of acceleration due to gravity is approximately 9.8 m/s². However, on different planets or celestial bodies, the acceleration due to gravity can be significantly different. For example, on the Moon, the acceleration due to gravity is about 1/6th of that on Earth, while on Jupiter, it is much stronger. Therefore, the value of acceleration due to gravity is specific to each celestial body and is not a universal constant.
5: What is the SI unit of gravitational acceleration?
Answer: The SI unit of gravitational acceleration is meters per second squared (m/s²). Gravitational acceleration represents the rate at which an object accelerates under the influence of gravity. It measures the change in velocity per unit of time and is expressed in terms of meters per second squared.
6: What is the value of g?
Answer: The value of “g” represents the acceleration due to gravity and varies depending on the location and altitude on Earth. The standard average value of gravitational acceleration on the surface of the Earth is approximately 9.8 m/s².
7: What factors does gravitational acceleration depend on?
Answer: The formula for gravitational acceleration is as follows:
g = G x M / r2
As we can see, Gravitational acceleration depends on several factors. Firstly, it is influenced by the mass of the celestial body. The greater the mass, the stronger the gravitational acceleration. Secondly, the distance from the center of the celestial body affects gravitational acceleration. It decreases as the distance increases. The gravitational constant, denoted as G, is another factor and its value is constant universally. Additionally, local variations in gravitational acceleration can occur due to differences in topography and density variations within Earth’s crust. Lastly, the presence of other celestial bodies nearby can influence gravitational acceleration through gravitational interactions.
8: Why is it called gravitation?
Answer: Gravitation is called so because it refers to the natural phenomenon of attraction between objects with mass. The term “gravitation” is derived from the Latin word “gravitas,” meaning “heaviness” or “weight.” It describes the force of attraction that exists between any two objects with mass, causing them to move towards each other. This force is commonly known as gravity and is responsible for many observable phenomena, such as the motion of planets, the falling of objects, and the dynamics of celestial bodies in the universe.





