Table of Contents
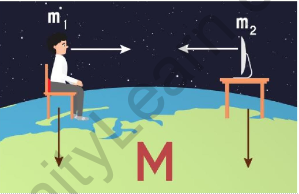
The gravitational force formula describes the attractive force between two objects with mass. It is given by Newton’s law of universal gravitation, which states that the gravitational force (F) between two objects is directly proportional to the product of their masses (m1 and m2) and inversely proportional to the square of the distance (r) between their centers.
The formula is expressed as F = G x (m1 x m2) / r2, where G is the gravitational constant. The gravitational force is always attractive, pulling objects toward each other. This formula helps in calculating the gravitational force between any two objects in the universe, providing insights into celestial motion, orbits, and the behavior of massive bodies.
What is Gravitational Force?
The gravitational force is the attractive force between any two objects with non-zero mass separated by a distance.
What is the Universal Law of Gravitation?
According to the universal law of gravitation, every object in the universe attracts every other object with a force, which is directly proportional to the product of their masses and inversely proportional to the square of the distance between them.
Let us try to understand this law.
Consider two objects A and B separated by a distance ‘d’. The distance between the centres is considered as the distance between the two objects. Let us assume that the mass of object A is 1 and that of object B is m2. As object A is bigger, let’s assume m1 > m2.
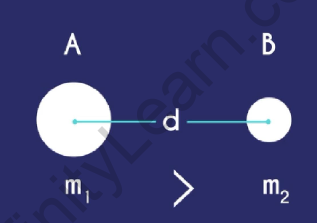
Two Objects Separated by a Distance
According to the universal law of gravitation,
![]()
And,
![]()
The given relationship can be represented as follows:
![]()
So, if the mass of any of the objects increases, the gravitational force will have more magnitude. More the distance between the two objects, the lesser the gravitational force.
The gravitational force formula can be written by introducing a proportionality constant ‘G’ as follows:
![]()
The proportionality constant G is called the universal gravitational constant. The universally accepted gravitational constant value is as follows:
G = 6.673 x 10-11 Nm2kg-2
Formula and Unit of Gravitational Force:
The formula for gravitational force is given by F = G x (m1 x m2) / r2, where F is the force, G is the gravitational constant, m1 and m2 are the masses, and r is the distance between them. The unit of gravitational force is the Newton (N).
Case study of Universal Law of Gravitation
Consider a case where you are sitting in front of your computer. Now, both you and the computer will exert a pulling force on each other but still neither of the two moves towards each other.
This is because there are other forces acting on you and the computer. For example, the gravitational force of the Earth is pulling you as well as the computer strongly towards itself. As a result, the force between you and the computer becomes negligible compared to it.
There is also a force of friction that is much more than the gravitational force between you and the computer.
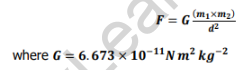
The value of G, that is the gravitational constant is very very small, and also the masses of the two objects are not big enough. Thus, the overall value of the gravitational force acting between the two is negligible.
Moreover, if we consider the gravitational force between you and the Earth or the computer and the Earth, then one of the masses will be the mass of the Earth, which is massive as compared to the other two masses. Therefore, the gravitational force pulling you and the computer down is much bigger than the force pulling you two towards each other.
Comparison of Gravitational Forces
Solved Examples of Gravitational Force Formula:
Example 1: Suppose we have two objects: Object A with a mass of 5 kg and Object B with a mass of 8 kg. The distance between their centers of mass is 2 meters. Calculate the gravitational force between them.
Solution:
Using Newton’s law of universal gravitation:
Given:
m1 = 5 kg
m2 = 8 kg
d = 2 meters
G = 6.67430 × 10(-11) N(m/kg)2 (gravitational constant)
Substituting the values into the formula:
F = (6.67430 × 10-11 x 5 x 8) / 22
F = (6.67430 × 10-11 x 40) / 4
F = 2.66852 × 10-10 N
Therefore, the gravitational force between Object A and Object B is approximately 2.66852 × 10-10 N.
Example 2: The mass of Zen is 70kg and that of Zara is 50kg. If the distance between them is 1 km, then calculate the force exerted by Zara on Zen.
Solution: Let be Zen’s mass, which is 70 kilograms, and be Zara’s mass, which is 50 kilograms. The distance d between them is 1 kilometer. Now, we need to convert the distance given in kilometers to meters. The distance d will equal 1000 meters. (G= 6.7 x 10-11 Nm2/kg-2)
Substituting the values in the formula:
![]()
We get the value of F as 2.345 x 10-13 N.
FAQ’s on Gravitational Force Formula
What is gravitational force?
Gravitational force is a fundamental force of nature that attracts objects with mass toward each other. It is responsible for the attraction between planets, stars, and other celestial bodies, as well as the force that keeps us grounded on Earth.
How do you use gravitational formula?
To use the gravitational force formula, you need to know the masses of the two objects and the distance between them. Plug these values into the formula F = G x (m1 x m2) / r2, where G is the gravitational constant. Calculate the product of the masses, divide it by the square of the distance, and multiply it by the gravitational constant to find the gravitational force between the two objects.
Is gravitational force equal on all objects?
To use the gravitational force formula, you need to know the masses of the two objects and the distance between them. Plug these values into the formula F = G x (m1 x m2) / r2, where G is the gravitational constant. Calculate the product of the masses, divide it by the square of the distance, and multiply it by the gravitational constant to find the gravitational force between the two objects.
Is gravitational force always present?
Yes, gravitational force is always present between objects that have mass. It is a fundamental force of nature that acts between any two objects with mass, regardless of their size or distance from each other. However, the strength of the gravitational force depends on the masses of the objects and the distance between them. In everyday life, we typically experience the gravitational force between the Earth and objects near its surface, which gives rise to phenomena such as weight and the motion of objects falling towards the ground.
Who discovered gravitational force?
The concept of gravitational force was first described by Sir Isaac Newton in the late 17th century. His work on the laws of motion and universal gravitation laid the foundation for our understanding of gravity.
How does gravitational force work?
Gravitational force works based on the principle that every object with mass attracts other objects with mass. The force of gravity between two objects depends on their masses and the distance between them. The greater the masses and the closer the objects, the stronger the gravitational force.
What is the formula for calculating gravitational force?
The formula to calculate gravitational force between two objects is given by Newton's law of universal gravitation: F = (G x m1 x m2) / r2, where F is the gravitational force, G is the gravitational constant, m1 and m2 are the masses of the two objects, and r is the distance between their centers of mass.
What is the gravitational constant?
The gravitational constant (G) is a fundamental constant in physics that appears in the formula for calculating gravitational force. It is approximately equal to 6.67430 × 10-11 N(m/kg)2.
Does gravitational force depend on the shape of an object?
No, gravitational force does not depend on the shape of an object. It depends solely on the masses of the objects and the distance between their centers of mass.
Does gravitational force act only on Earth?
No, gravitational force is present everywhere in the universe. It acts between all objects that have mass. However, the strength of the gravitational force decreases with increasing distance.
Can gravitational force be repulsive?
No, gravitational force is always attractive. It always pulls objects toward each other and never pushes them apart.
How does distance affect gravitational force?
Gravitational force decreases with increasing distance between objects. It follows an inverse square law, meaning that if you double the distance between two objects, the gravitational force between them becomes four times weaker.









