Table of Contents
- Frustum of a Cone
- Surface Area of Frustum of a Cone
- Volume of Frustum of a Cone
- Summary
- What’s Next?
In the previous segment, we learnt about the conversion of solids. In this segment, we will learn about the Frustum of a cone.
What is the Frustum of a cone?
When a cone is cut into two parts by a plane parallel to the base of the cone: the upper part of the cone remains the same in shape and the bottom part makes a Frustum.
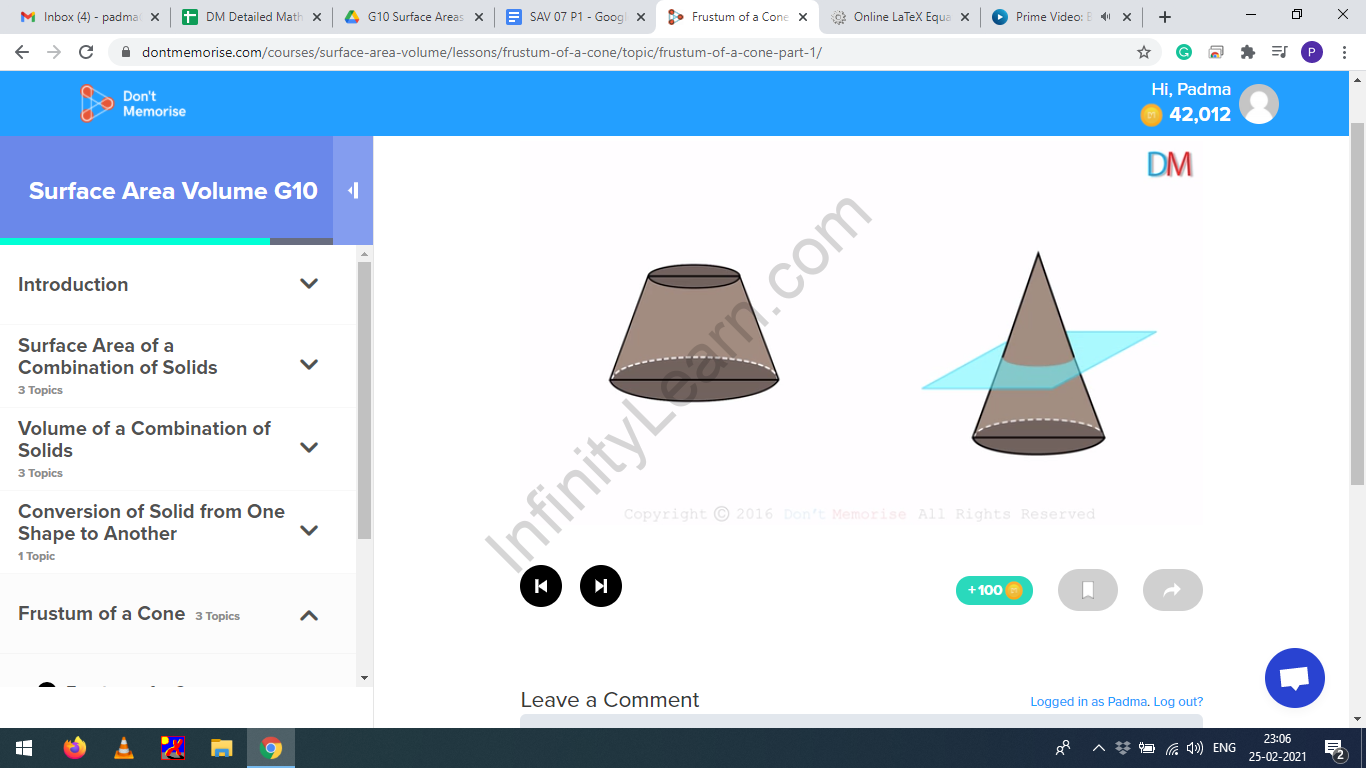
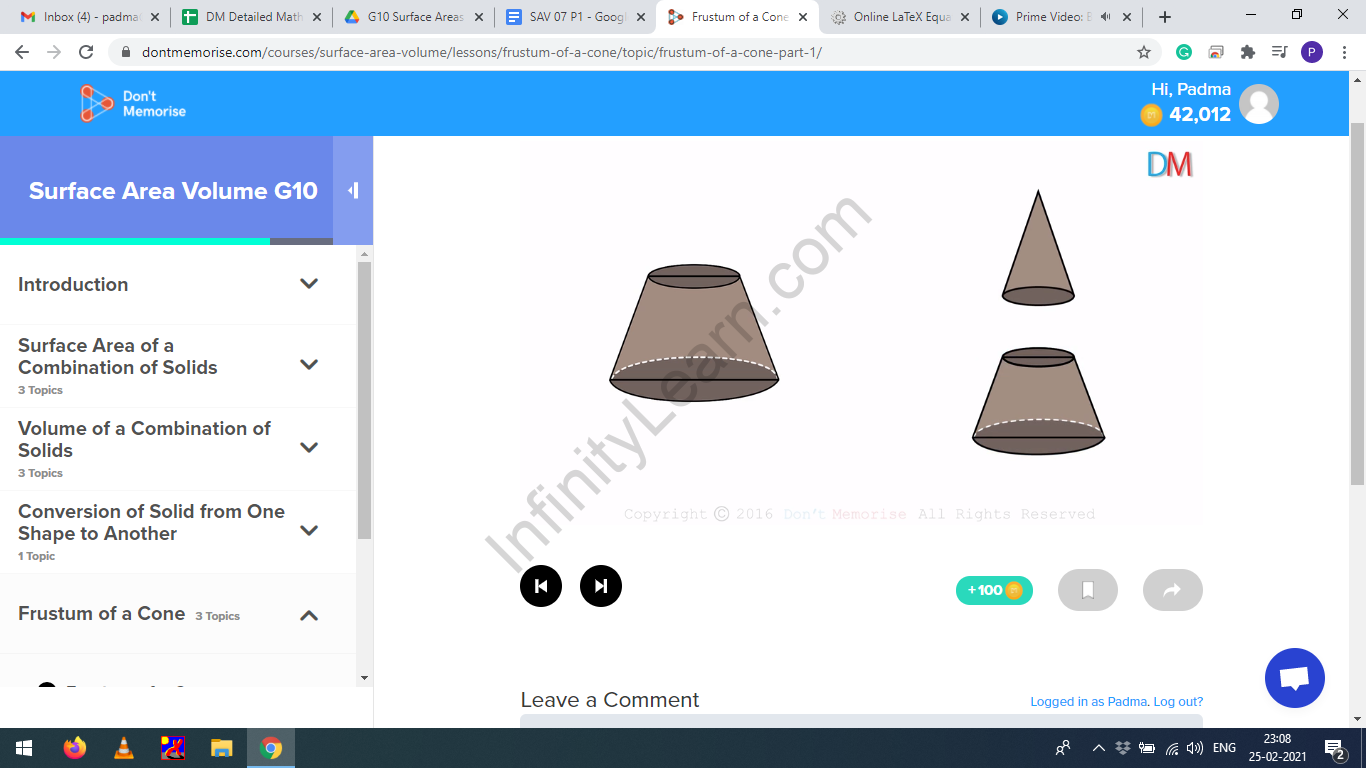
Frustum
Frustum of a cone
Consider the figure below:
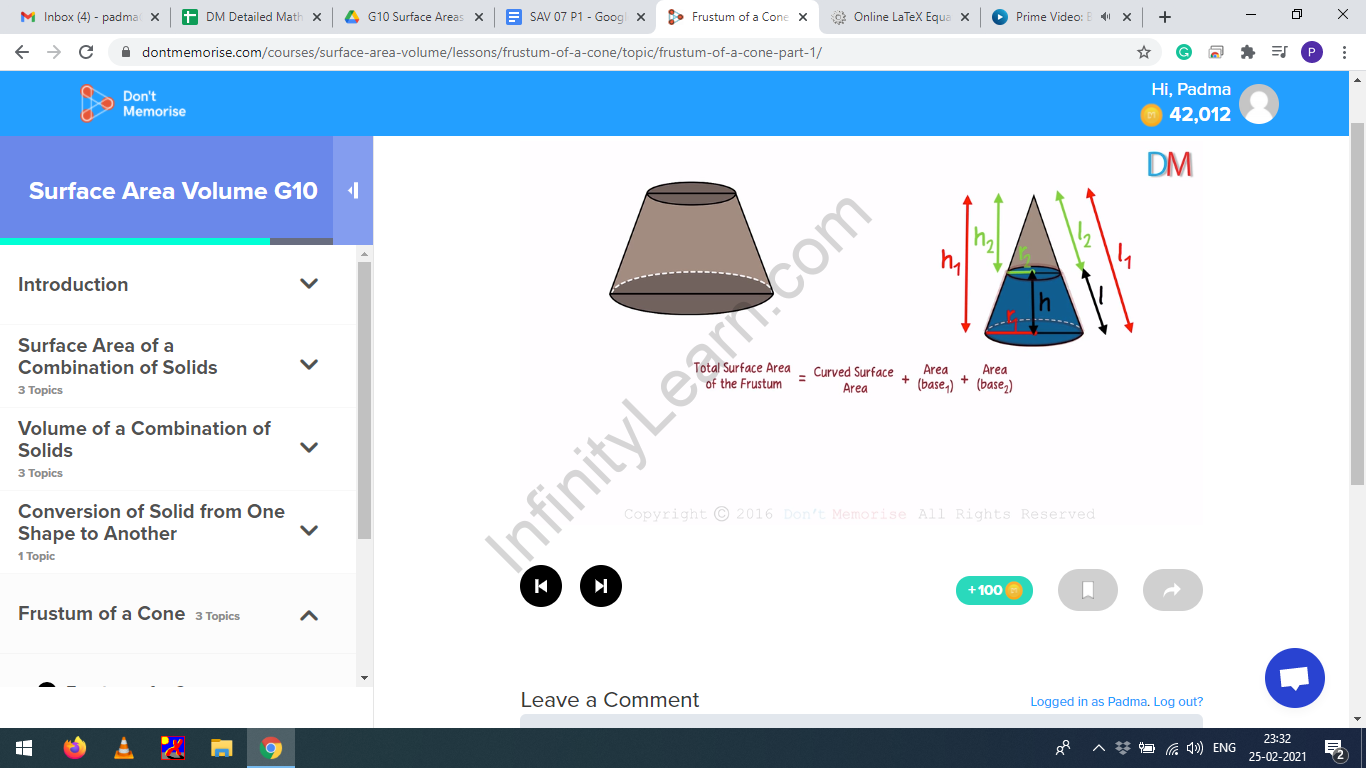
Figure 1
Let be the radius, slant height, and height of the bigger cone respectively and be the radius, slant height, and height of the smaller cone respectively. Let l, h be the slant height and height of the frustum respectively.
What is the surface area of the frustum of a cone?
CSA of frustum = CSA of bigger cone – CSA of smaller cone
So, CSA of frustum =
∴ CSA of frustum
Base 1 is the bigger circle and Base 2 is the smaller circle.
∴ Area of base 1 =
and Area of base 2
Total surface area of frustum = Curved surface area + Area of base 1 + Area of base 2
∴ Total surface area of frustum =
∴ Total surface area of frustum
What is the volume of a frustum of a cone?
Volume of the Frustum = Volume (Bigger cone) – Volume (Smaller cone)
∴ Volume of the Frustum
∴ Volume of the Frustum
Summary
| Frustum of a Cone | Bottom part of the cone that is formed when a cone is cut by a plane parallel to its base |
| Surface Area of Frustum of Cone |
|
| Volume of Frustum of Cone |
|
What’s next?
In the next segment of Class 10 Maths, we will look at the parameters of the frustum in detail.



