Table of Contents
- Conversion of Solids – Examples
- Conversion of Solids – Problems
- What’s Next?
In the previous segment, we derived the formula for surface area and volume of a gulab jamun. In this segment, we will learn about conversion of solids from one shape to another.
Conversion of solids – examples
Water occupies the shape of the container it is poured in. So, if a cuboid is filled with water, the water takes the shape of the cuboid. But when the same water is poured into a hemispherical ball, it has the shape of a hemisphere.
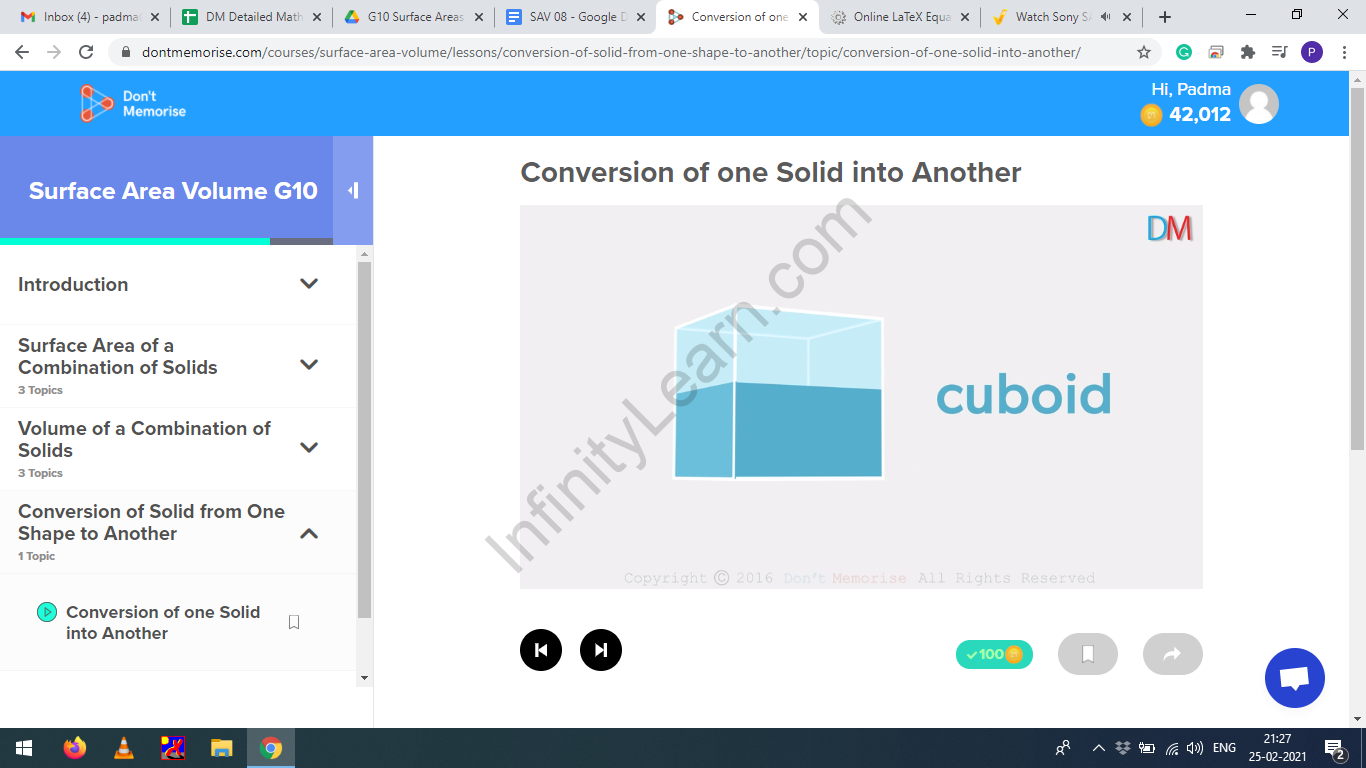
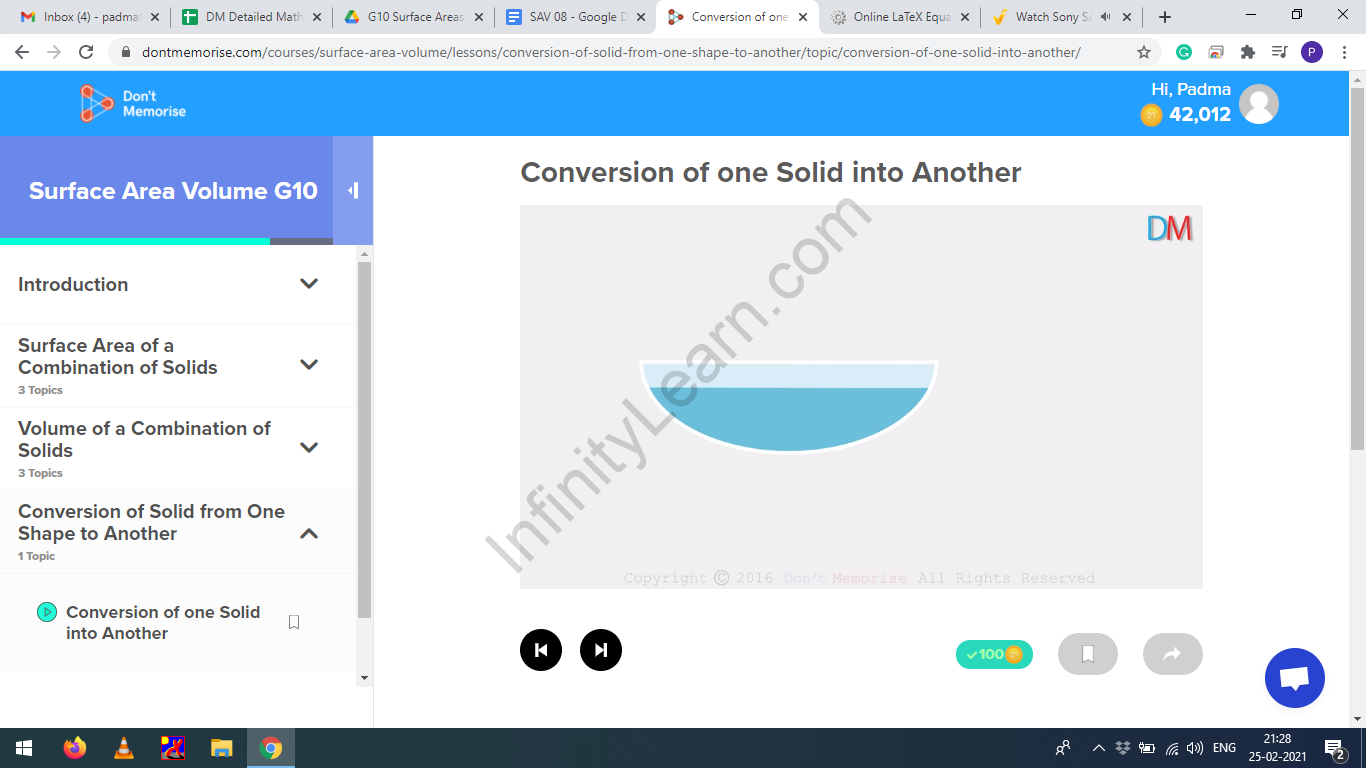
=
Volume of water in cuboid = Volume of water in hemisphere
However the amount of water is the same in both the containers. That is the volume of the water is unchanged.
Let us look at another example.
When a candle of a cylindrical shape is melted and the molten wax is poured into a conical flask, the shape of the candle changes from a cylinder to a cone. But the volume of wax remains the same.
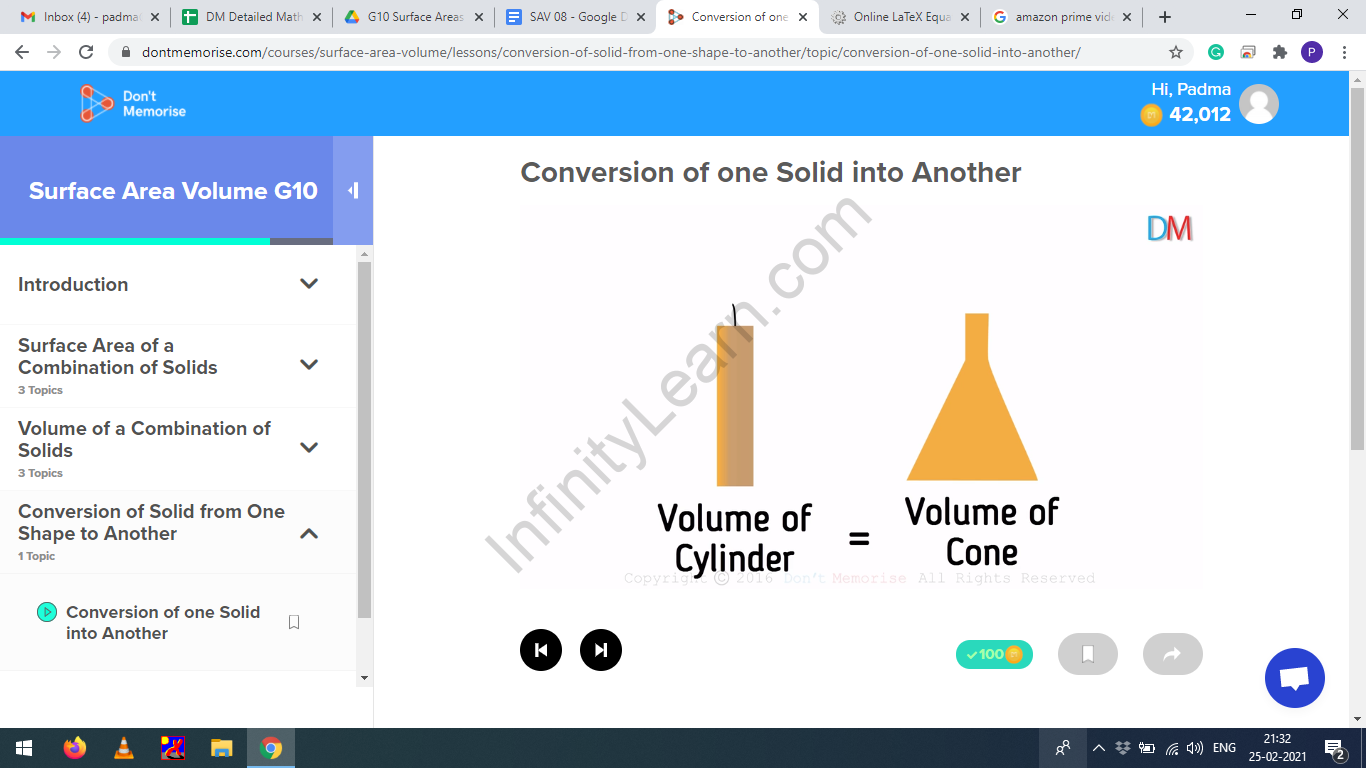
Volume of cylinder = Volume of cone
Problem
Q. A container shaped like a right circular cylinder having diameter 24 cm and height 15 cm is full of ice cream. The ice cream is to be filled into identical cones of height 8 cm and diameter 4 cm, having a hemispherical shape on the top. Find the number of such cones which can be filled with ice cream.
Solution:
Let the volumes of the cylinder, cone and hemisphere be respectively.
Let be respectively the diameters of the cylinder and the cone and be their respective radii.
The ice cream from the cylinder is filled into cones.
So, the volume of the ice cream will be equal to the volume of the containers.
volume of the ice cream in the cylinder = volume of the cylinder=
In the cones the ice cream filled with a hemispherical top.
Therefore, volume of ice cream in the cone = volume of cone + volume of hemisphere =
The parameters given are as below:
| Cylinder | Cone | Hemisphere |
| The base of the hemisphere is congruent to the cone’s base. Therefore, its radius is same as that of the cone |
If the maximum number of cones for filling the ice creams is n,
then,
Thus, the ice cream can be filled in 135 cones.
In the next segment of Class 10, we will learn about Frustum of a cone.



