Snell’s Law Formula

Introduction:

Snell’s law, also known as the law of refraction, is a fundamental principle in optics that describes how light waves change direction when they pass through the interface between two different transparent media. The formula for Snell’s law is n1sin(θ1) = n2sin(θ2), where n1 and n2 are the indices of refraction of the two media, and θ1 and θ2 are the angles of incidence and refraction, respectively. This equation quantitatively relates the angles of incidence and refraction to the refractive indices, providing a mathematical framework to understand and predict the bending of light at the interface. Snell’s law is widely applied in various optical phenomena and is essential in the design and analysis of lenses, prisms, and other optical devices.

The laws of refraction are as follows:

The incident ray, the refracted ray, and the normal at the point of incidence lie on the same plane.

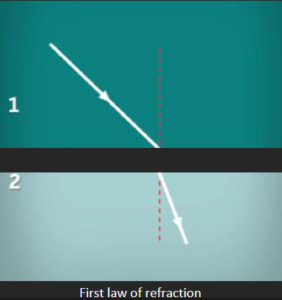
The refractive index of a refractive medium with respect to the incident medium is equal to the ratio of the sine of the incident angle to the sine of the refractive angle. This is also known as Snell’s law.

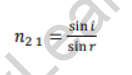
Snell’s Law Formula:

Consider a ray of light travelling from medium 1 to medium 2. Let the angle of incidence be i and the angle of refraction be r. Let the speed of light in medium 1 be v1 and that in medium 2 be v2. Let n21 be the refractive index of medium 2 with respect to medium 1.

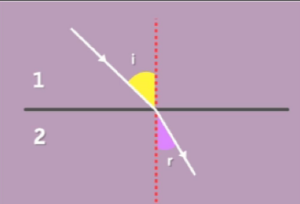
Then, according to Snell’s law,

Also, by definition of refractive index,

Thus, from statement (i) and (ii),

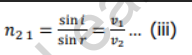
Let n1 and n2 be the absolute refractive indices of medium 1 and medium 2 respectively. If the velocity of light in vacuum is c, then,

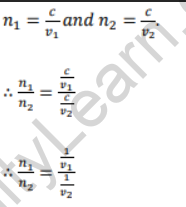
From statements (iii) and (iv), Snell’s law can be expressed as

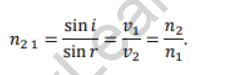
Key points about Snell’s Law:

• Snell’s law applies to the refraction of light when it passes from one medium to another, such as air to water or glass to air.
• The refractive index of a medium is a measure of how much the speed of light is reduced when it enters that medium.
• The angle of incidence is the angle between the incident ray and the normal (a line perpendicular to the interface between the two media).
• The angle of refraction is the angle between the refracted ray and the normal.
• Snell’s law implies that light bends towards the normal when it enters a medium with a higher refractive index and away from the normal when it enters a medium with a lower refractive index.
• When light passes from a medium with a higher refractive index to a medium with a lower refractive index, there exists a critical angle beyond which total internal reflection occurs.

Solved Examples on Snell’s Law Formula:

Example 1: Light enters from air to glass having a refractive index of 1.50. What is the speed of light in glass? (The speed of light in vacuum = 3 × 108 m/s).

Given:

Let air and glass be considered as medium 1 and medium 2 respectively. Refractive index of glass w.r.t. air (n21) = 1.50

Speed of light in vacuum (c) = 3 × 108 m/s

To find:

Speed of light in glass (2)

Formula:

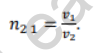
Answer:

By Snell’s law,

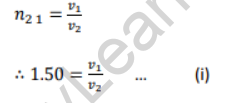
The speed of light in air is very close to the speed of light in vacuum. Thus, v1 = 3 × 108 m/s

Substituting in statement (i),

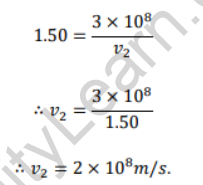
Thus the light will travel in the glass at a speed of 2 × 108 m/s.

Example 2: A light ray travels from water (refractive index = 1.33) into diamond (refractive index = 2.42). If the angle of incidence is 40 degrees, calculate the angle of refraction.

Solution:

Given:

n₁ (refractive index of water) = 1.33

n₂ (refractive index of diamond) = 2.42

θ₁ (angle of incidence) = 40 degrees

Using Snell’s law we can write,

n₁ x sin(θ₁) = n₂ x sin(θ₂)

Substituting the given values:

1.33 x sin(40) = 2.42 x sin(θ₂)

sin(θ₂) = (1.33 x sin(40)) / 2.42

sin(θ₂) ≈ 0.706

Taking the inverse sine (arcsine) of both sides:

θ₂ = arcsine(0.706)

Using a calculator:

θ₂ ≈ 44.1 degrees

Therefore, the angle of refraction is approximately 44.1 degrees.

Frequently asked questions on Snell’s Law Formula:

1: What is Snell’s law and law of refraction?

Answer: Snell’s law, also known as Snell-Descartes law, is a fundamental principle in optics that describes the behavior of light as it passes from one medium to another. It relates the angles of incidence and refraction to the refractive indices of the two media involved.

2: What is the mathematical expression of Snell’s law?

Answer: Snell’s law is expressed as: n₁ x sin(θ₁) = n₂ x sin(θ₂), where n₁ and n₂ are the refractive indices of the incident and refracting media, respectively, and θ₁ and θ₂ are the angles of incidence and refraction, respectively.

3: What is the refractive index?

Answer: The refractive index is a measure of how much the speed of light is reduced when it enters a particular medium compared to its speed in a vacuum. It is denoted by the symbol ‘n’ and is defined as the ratio of the speed of light in a vacuum to the speed of light in the medium.

4: What is V1 and V2 in Snell’s law?

Answer: In Snell’s law, V1 and V2 represent the velocities of light in two different media. The velocities of light in different media are related to the refractive indices of those media, as the refractive index is defined as the ratio of the speed of light in vacuum to the speed of light in the medium. Therefore, V1 and V2 can be understood as the speeds at which light propagates through the respective media. The ratio of the velocities, or equivalently the refractive indices, is used in Snell’s law to determine how the direction of light changes when it passes from one medium to another.

5: What are the two types of refractive index?

Answer: The two types of refractive index commonly referred to are the absolute refractive index and the relative refractive index.

1. Absolute Refractive Index: The absolute refractive index is a measure of how much a particular material bends light when compared to a vacuum or air. It is the ratio of the speed of light in vacuum to the speed of light in the material. The absolute refractive index is denoted by the symbol “n” and is dimensionless.

1. Relative Refractive Index: The relative refractive index is the ratio of the absolute refractive index of one material to another. It represents the change in the speed of light as it passes from one medium to another. The relative refractive index is also dimensionless and is denoted by the symbol “n1/n2”, where “n1” and “n2” represent the absolute refractive indices of the two media.

6: What is n1 and n2 in Snell’s law?

Answer: In Snell’s law, n1 and n2 represent the refractive indices of two different media through which light is passing. n1 refers to the refractive index of the initial medium (or incident medium), while n2 refers to the refractive index of the final medium (or refractive medium). The refractive index of a medium is a measure of how much the speed of light is reduced when it passes through that medium compared to its speed in a vacuum. The ratio of the refractive indices, n1/n2, is used in Snell’s law to determine how the direction of light is refracted or bent as it transitions from one medium to another.

7: What is the SI unit of refractive index?

Answer: The SI unit of refractive index is dimensionless, as it is a ratio of the speed of light in a vacuum to the speed of light in a given medium. It does not have a specific unit associated with it.

8: Why is it called Snell’s law?

Answer: Snell’s law is named after the Dutch mathematician and astronomer Willebrord Snellius (also known as Snell) who first formulated this law in the 17th century. Snell’s law describes the relationship between the angles of incidence and refraction when light passes through the boundary between two different transparent media. The law is commonly used to understand the bending of light as it passes through materials with different refractive indices.

9: What happens to light when it passes from one medium to another?

Answer: When light passes from one medium to another, it can change direction and speed. This change is known as refraction. The bending of light occurs due to the change in its speed as it moves from a medium with one refractive index to another with a different refractive index.

10: What is the relationship between the angles of incidence and refraction?

Answer: The relationship between the angles of incidence and refraction is given by Snell’s law. It states that the ratio of the sines of the angles of incidence and refraction is equal to the ratio of the refractive indices of the two media.

11: What happens if the angle of incidence is greater than the critical angle?

Answer: If the angle of incidence is greater than the critical angle, total internal reflection occurs. This means that all of the light is reflected back into the medium of higher refractive index, and none of it is transmitted into the second medium.