Practice Test on Math Relations helps students to get a grip on the concept of Relations. Get to know about various questions like Representation of a Relation, finding Domain and Range, Cartesian Product of Two Sets, etc. Learn topics of Relations easily and solve the questions in Math Relation Worksheet whenever you want. Identify the knowledge gap and concentrate on the areas you are lagging and improvise on them.
1. Let A = {3, 4, 5, 6} and B = {x, y, z}. Let R be a relation from A into B defined by R = {(3, x), (4, y), (5, z), (6, x), (6, y)} find the domain and range of R.
Solution:
Given Relation R = {(3, x), (4, y), (5, z), (6, x), (6, y)}
The domain is the first component of the ordered pairs in the Relation R whereas Range is the second component of the ordered pairs. Repetition is not allowed.
Domain = {3, 4, 5, 6}
Range = {x, y, z}
2. Find the Domain and Range Value from the given tabular form
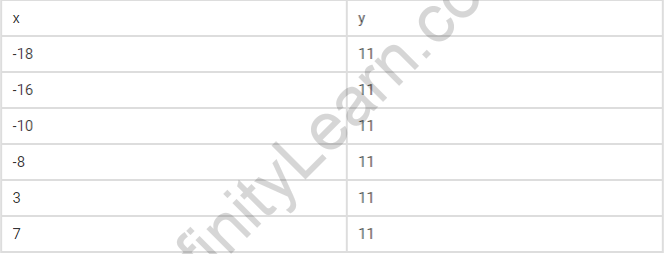
Solution:
Domain = {-18, -16, -10, -8, 3, 7}
Range = {11}
3. Determine the domain and range of the given functions:
{7, -9), (1, -5), (4, 3), (8, 5), (8, -14)}
Solution:
Given Relation = {7, -9), (1, -5), (4, 3), (8, 5), (8, -14)}
The domain is the first component of the ordered pairs in the Relation R whereas Range is the second component of the ordered pairs. Repetition is not allowed.
Domain = {7, 1, 4, 8} Range R = {-9, -5, 3, 5, -14}
4. What is the domain of this set of ordered pairs?
{ (3, 7), (4, -3), (1, 5), (-10, 6) }
Solution:
The domain is the first component in the ordered pairs.
Domain = { 3, 4, 1, -10}
5. If Set A = { 3, 4, 5}, Set B = {x, y, z} find the Cartesian Product of Two Sets?
Solution:
Set A = { 3, 4, 5}, Set B = {x, y, z}
AxB = {(3, x), (4, x), (5, x), (3, y), (4, y), (5, y), (3, z), (4, z), (5, z)}
6. Which of the following statement is true
a) All the relations are functions.
b) In every relation, each input value has exactly one output value.
c) A relation is defined as a set of input and output values that are related in some way.
d) All the above statements are true.
Solution:
c) A relation is defined as a set of input and output values that are related in some way.
7. The following Arrow Diagram shows a Relation from Set A to Set B. Find the Domain and Range?
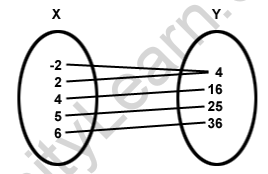
Solution:
The domain is the first component of the ordered pairs in the Relation R whereas Range is the second component of the ordered pairs. Repetition is not allowed.
Domain = { -2, 2, 4, 5, 6}
Range = { 4, 16, 25, 36}
8. The below figure shows a relation between Set x and Set y. Write the same in Roster Form, Set Builder Form, and find the domain and Range?
Solution:
In the Set Builder Form R = {(x, y): x is the square of y, x ∈ X, y ∈ Y}
In Roster Form R = {(2, 1)(4, 2)}
Domain = {2, 4}
Range = {1, 2}
9. What can you say about the ordered pairs (x, y) and (y, x)?
Solution:
Ordered Pairs (x, y) ≠ (y, x).
In case of Ordered Pairs Order Matters.
10. If A × B = {(a, 2); (a, 6); (a, 3); (b, 3); (b, 6); (b, 2)}, find B × A.
Solution:
Given AxB = {(a, 2); (a, 6); (a, 3); (b, 3); (b, 6); (b, 2)}
BxA = {(2, a); (6, a); (3, a); (3, b); (6, b); (2, b)}



