For Class 10 Mathematics Chapter 9, “Some Applications of Trigonometry,” important questions are available here to help students prepare for the board exams. These questions follow the latest CBSE pattern and align with the revised syllabus. Students preparing for the CBSE 2022-2023 Mathematics exam are encouraged to practice these important questions on “Some Applications of Trigonometry” for Class 10. By solving these questions, students can improve their understanding and score well in the questions related to this chapter.
Applications of Trigonometry Class 10 Important Questions
Q 1. The ratio of the height of a tower and length of its shadow on the ground is √3 : 1 what is the angle of elevation of the sun ? [CBSE 2017]
Answer:
Let TW be tower and WS be its shadow.
Let ∠TSW = θ (angle of elevation)

tan θ = TW WS=3√1
⇒ tan θ = √3
⇒ θ ⇒
Q 2: The shadow of a tower standing on level ground is found to be 40 m longer when the Sun’s altitude is 30° than when it is 60°. Find the height of the tower.
Answer: Let AB be the tower and BC be the length of its shadow when the sun’s altitude (angle of elevation from the top of the tower to the tip of the shadow) is 60° and DB be the length of the shadow when the angle of elevation is 30°.
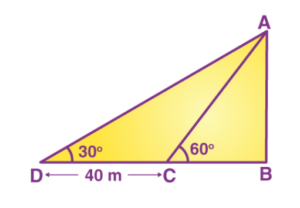
Let us assume, AB = h m, BC = x m
DB = (40 +x) m
In the right triangle ABC,
tan 60° = AB/BC
√3 = h/x
h = √3 x……….(i)
In the right triangle ABD,
tan 30° = AB/BD
1/√3 =h/(x + 40) ……..(ii)
From (i) and (ii),
x(√3 )(√3 ) = x + 40
3x = x + 40
2x = 40
x = 20
Substituting x = 20 in (i),
h = 20√3
Hence, the height of the tower is 20√3 m.
Q 3: From the top of a 7 m high building, the angle of elevation of the top of a cable tower is
60° and the angle of depression of its foot is 45°. Determine the height of the tower.
Solution:
Let AB be the height of the building and CE be the height of the tower.
Also, A be the point from where the elevation of the tower is 60° and the angle of depression of its foot is 45°.
EC = DE + CD
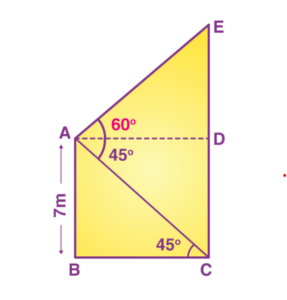
From the figure,
CD = AB = 7 m
BC = AD
In right ΔABC,
tan 45° = AB/BC
1 = 7/BC
BC = 7 {since BC = AD}
Thus, AD = 7 m
In right triangle ADE,
tan 60° = DE/AD
√3 = DE/7
⇒ DE = 7√3 m
EC = DE + CD = (7√3 + 7) = 7(√3 + 1)
Therefore, the height of the tower is 7(√3 + 1) m.
Q 4: Two poles of equal heights are standing opposite each other on either side of the road, which is 80 m wide. From a point between them on the road, the angles of elevation of the top of the poles are 60° and 30°, respectively. Find the height of the poles and the distances of the point from the poles.
Solution:
Let AB and CD be the poles of equal height.
O is the point between them from where the height of elevation is taken. BD is the distance between the poles.
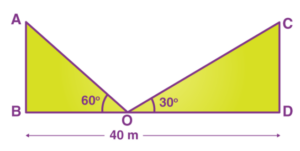
As per the above figure, AB = CD,
OB + OD = 80 m
Now,
In right ΔCDO,
tan 30° = CD/OD
1/√3 = CD/OD
CD = OD/√3 … (1)
In right ΔABO,
tan 60° = AB/OB
√3 = AB/(80-OD)
AB = √3(80-OD)
AB = CD (Given)
√3(80-OD) = OD/√3 (Using equation (1))
3(80-OD) = OD
240 – 3 OD = OD
4 OD = 240
OD = 60
Substituting the value of OD in equation (1)
CD = OD/√3
CD = 60/√3
CD = 20√3 m
Also,
OB + OD = 80 m
⇒ OB = (80-60) m = 20 m
Therefore, the height of the poles are 20√3 m and the distance from the point of elevation are 20 m and 60 m respectively.
Q 5: A circus artist is climbing a 20 m long rope, which is tightly stretched and tied from the top of a vertical pole to the ground. Find the height of the pole, if the angle made by the rope with the ground level is 30°.
Solution:
Let AB be the vertical pole and AC be the length of the rope.
Also, the angle of elevation = ∠ACB = 30°
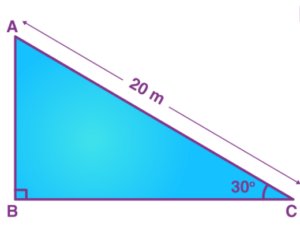
In right triangle ABC,
sin 30 = AB/AC
1/2 = AB/20
AB = 20/2 = 10
Therefore, the height of the vertical pole is 10 m.
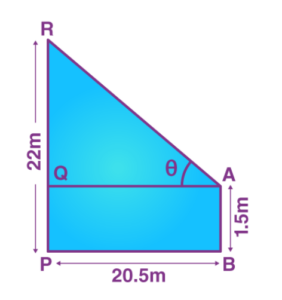
Q 6: An observer 1.5 metres tall is 20.5 metres away from a tower 22 metres high. Determine the angle of elevation of the top of the tower from the eye of the observer.
Solution:
Let AB be the height of the observer and PR be the height of the tower.
Also, PB is the distance between the foot of the tower and the observer.
Consider θ as the angle of elevation of the top of the tower from the eye of the observer.
Q 7: The angle of elevation of the top of a tower from a certain point is 30°. If the observer moves 20 metres towards the tower, the angle of elevation of the top increases by 15°. Find the height of the tower.
Solution:
Let AB be the height of the tower.
AB = h
The angle of elevation of the top of a tower from point P is 30°, i.e. ∠APB = 30°.
Given that, when the observer moves 20 metres towards the tower, the angle of elevation of the top increases by 15°.
Thus, PQ = 20 m
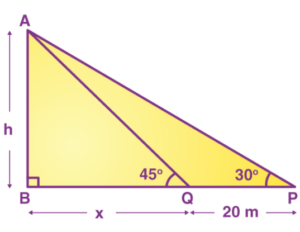
Also, ∠AQB = 30° + 15° = 45°.
QB = x
In right triangle ABQ,
tan 45° = AB/QB
1 = h/x
h = x….(i)
In right triangle ABP,
tan 30° = AB/PB
1/√3 = h/(x + 20)
x + 20 = √3h {from (i)}
h + 20 = √3h
√3h – h = 20
h = 20/(√3 – 1)
h = [20/(√3 – 1)] × [(√3 + 1)/(√3 + 1)]
= 20(√3 + 1)/(3 – 1)
= 20(√3 + 1)/2
= 10(√3 + 1)
Therefore, the height of the tower is 10(√3 + 1) m.




