CBSE Class 12 Maths Notes Chapter 5 Continuity and Differentiability
Continuity at a Point: A function f(x) is said to be continuous at a point x = a, if
Left hand limit of f(x) at(x = a) = Right hand limit of f(x) at (x = a) = Value of f(x) at (x = a)
i.e. if at x = a, LHL = RHL = f(a)
where, LHL = \(\lim _{ x\rightarrow { a }^{ – } }{ f(x) }\) and RHL = \(\lim _{ x\rightarrow { a }^{ + } }{ f(x) }\)
Note: To evaluate LHL of a function f(x) at (x = o), put x = a – h and to find RHL, put x = a + h.
Continuity in an Interval: A function y = f(x) is said to be continuous in an interval (a, b), where a < b if and only if f(x) is continuous at every point in that interval.
- Every identity function is continuous.
- Every constant function is continuous.
- Every polynomial function is continuous.
- Every rational function is continuous.
- All trigonometric functions are continuous in their domain.
Standard Results of Limits
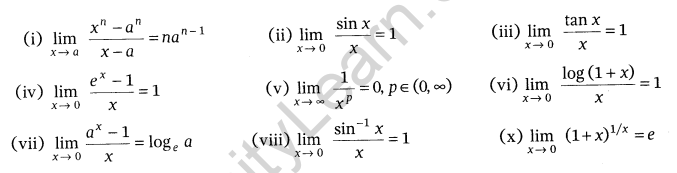
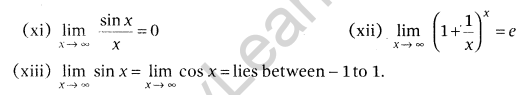
Algebra of Continuous Functions
Suppose f and g are two real functions, continuous at real number c. Then,
- f + g is continuous at x = c.
- f – g is continuous at x = c.
- f.g is continuous at x = c.
- cf is continuous, where c is any constant.
- (\(\frac { f }{ g }\)) is continuous at x = c, [provide g(c) ≠ 0]
Suppose f and g are two real valued functions such that (fog) is defined at c. If g is continuous at c and f is continuous at g (c), then (fog) is continuous at c.
If f is continuous, then |f| is also continuous.
Differentiability: A function f(x) is said to be differentiable at a point x = a, if
Left hand derivative at (x = a) = Right hand derivative at (x = a)
i.e. LHD at (x = a) = RHD (at x = a), where Right hand derivative, where
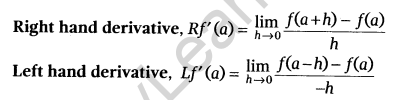
Note: Every differentiable function is continuous but every continuous function is not differentiable.
Differentiation: The process of finding a derivative of a function is called differentiation.
Rules of Differentiation
Sum and Difference Rule: Let y = f(x) ± g(x).Then, by using sum and difference rule, it’s derivative is written as
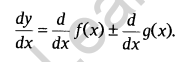
Product Rule: Let y = f(x) g(x). Then, by using product rule, it’s derivative is written as
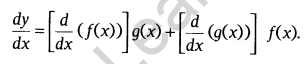
Quotient Rule: Let y = \(\frac { f(x) }{ g(x) }\); g(x) ≠ 0, then by using quotient rule, it’s derivative is written as
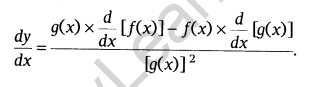
Chain Rule: Let y = f(u) and u = f(x), then by using chain rule, we may write
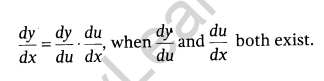
Logarithmic Differentiation: Let y = [f(x)]g(x) ..(i)
So by taking log (to base e) we can write Eq. (i) as log y = g(x) log f(x). Then, by using chain rule
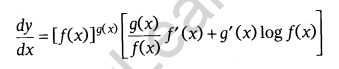
Differentiation of Functions in Parametric Form: A relation expressed between two variables x and y in the form x = f(t), y = g(t) is said to be parametric form with t as a parameter, when
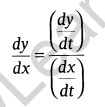
(whenever \(\frac { dx }{ dt } \neq 0\))
Note: dy/dx is expressed in terms of parameter only without directly involving the main variables x and y.
Second order Derivative: It is the derivative of the first order derivative.
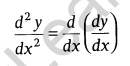
Some Standard Derivatives

Rolle’s Theorem: Let f : [a, b] → R be continuous on [a, b] and differentiable on (a, b) such that f(a) = f(b), where a and b are some real numbers. Then, there exists at least one number c in (a, b) such that f'(c) = 0.
Mean Value Theorem: Let f : [a, b] → R be continuous function on [a, b]and differentiable on (a, b). Then, there exists at least one number c in (a, b) such that
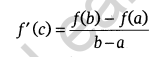
Note: Mean value theorem is an expansion of Rolle’s theorem.
Some Useful Substitutions for Finding Derivatives Expression






