Lines and Angles Class 7 Extra Questions Maths Chapter 5

Lines and Angles Class 7 Extra Questions Maths Chapter 5

Extra Questions for Class 7 Maths Chapter 5 Lines and Angles

Lines and Angles Class 7 Extra Questions Very Short Answer Type

Question 1.
Find the angles which is \(\frac { 1 }{ 5 }\) of its complement.
Solution:
Let the required angle be x°
its complement = (90 – x)°
As per condition, we get

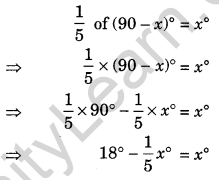
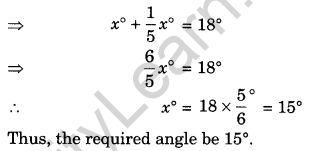
Question 2.
Find the angles which is \(\frac { 2 }{ 3 }\) of its supplement.
Solution:
Let the required angle be x°.
its supplement = (180 – x)°
As per the condition, we get
\(\frac { 2 }{ 3 }\) of (180 – x)° = x°

Question 3.
Find the value of x in the given figure.

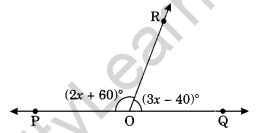
Solution:
∠POR + ∠QOR = 180° (Angles of linear pair)
⇒ (2x + 60°) + (3x – 40)° = 180°
⇒ 2x + 60 + 3x – 40 = 180°
⇒ 5x + 20 = 180°
⇒ 5x = 180 – 20 = 160
⇒ x = 32
Thus, the value of x = 32.

Question 4.
In the given figure, find the value of y.

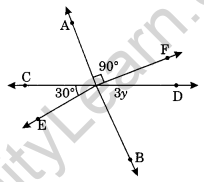
Solution:
Let the angle opposite to 90° be z.
z = 90° (Vertically opposite angle)
3y + z + 30° = 180° (Sum of adjacent angles on a straight line)
⇒ 3y + 90° + 30° = 180°
⇒ 3y + 120° = 180°
⇒ 3y = 180° – 120° = 60°
⇒ y = 20°
Thus the value of y = 20°.

Question 5.
Find the supplements of each of the following:
(i) 30°
(ii) 79°
(iii) 179°
(iv) x°
(v) \(\frac { 2 }{ 5 }\) of right angle
Solution:
(i) Supplement of 30° = 180° – 30° = 150°
(ii) Supplement of 79° = 180° – 79° = 101°
(iii) Supplement of 179° = 180° – 179° = 1°
(iv) Supplement of x° = (180 – x)°
(v) Supplement of \(\frac { 2 }{ 5 }\) of right angle
= 180° – \(\frac { 2 }{ 5 }\) × 90° = 180° – 36° = 144°

Question 6.
If the angles (4x + 4)° and (6x – 4)° are the supplementary angles, find the value of x.
Solution:
(4x + 4)° + (6x – 4)° = 180° (∵ Sum of the supplementary angle is 180°)
⇒ 4x + 4 + 6x – 4 = 180°
⇒ 10x = 180°
⇒ x = 18°
Thus, x = 18°

Question 7.
Find the value of x.

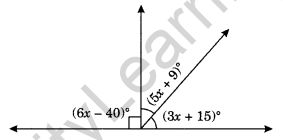
Solution:
(6x – 40)° + (5x + 9)° + (3x + 15) ° = 180° (∵ Sum of adjacent angles on straight line)
⇒ 6x – 40 + 5x + 9 + 3x + 15 = 180°
⇒ 14x – 16 = 180°
⇒ 14x = 180 + 16 = 196
⇒ x = 14
Thus, x = 14

Question 8.
Find the value of y.

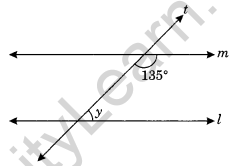
Solution:
l || m, and t is a transversal.
y + 135° = 180° (Sum of interior angles on the same side of transversal is 180°)
⇒ y = 180° – 135° = 45°
Thus, y = 45°

Lines and Angles Class 7 Extra Questions Short Answer Type

Question 9.
Find the value ofy in the following figures:

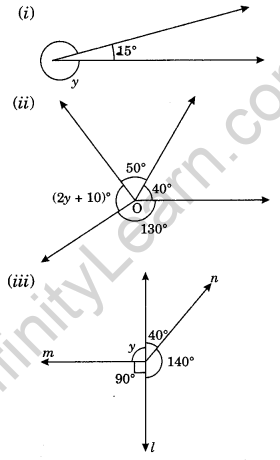
Solution:
(i) y + 15° = 360° (Sum of complete angles round at a point)
⇒ y = 360° – 15° = 345°
Thus, y = 345°
(ii) (2y + 10)° + 50° + 40° + 130° = 360° (Sum of angles round at a point)
⇒ 2y + 10 + 220 = 360
⇒ 2y + 230 = 360
⇒ 2y = 360 – 230
⇒ 2y = 130
⇒ y = 65
Thus, y = 65°
(iii) y + 90° = 180° (Angles of linear pair)
⇒ y = 180° – 90° = 90°
[40° + 140° = 180°, which shows that l is a straight line]

Question 10.
In the following figures, find the lettered angles.

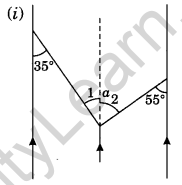
Solution:
(i) Let a be represented by ∠1 and ∠2
∠a = ∠1 + ∠2
∠1 = 35° (Alternate interior angles)
∠2 = 55° (Alternate interior angles)
∠1 + ∠2 = 35° + 55°
∠a = 90°
Thus, ∠a = 90°

Question 11.
In the given figure, prove that AB || CD.

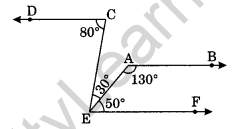
Solution:
∠CEF = 30° + 50° = 80°
∠DCE = 80° (Given)
∠CEF = ∠DCE
But these are alternate interior angle.
CD || EF ……(i)
Now ∠EAB = 130° (Given)
∠AEF = 50° (Given)
∠EAB + ∠AEF = 130° + 50° = 180°
But these are co-interior angles.
AB || EF …(ii)
From eq. (i) and (ii), we get
AB || CD || EF
Hence, AB || CD
Co-interior angles/Allied angles: Sum of interior angles on the same side of transversal is 180°.

Question 12.
In the given figure l || m. Find the values of a, b and c.

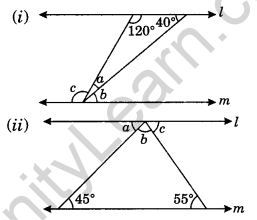
Solution:
(i) We have l || m
∠b = 40° (Alternate interior angles)
∠c = 120° (Alternate interior angles)
∠a + ∠b + ∠c = 180° (Sum of adjacent angles on straight angle)
⇒ ∠a + 40° + 120° = 180°
⇒ ∠a + 160° = 180°
⇒ ∠a = 180° – 160° = 20°
Thus, ∠a = 20°, ∠b = 40° and ∠c = 120°.
(ii) We have l || m
∠a = 45° (Alternate interior angles)
∠c = 55° (Alternate interior angles)
∠a + ∠b + ∠c = 180° (Sum of adjacent angles on straight line)
⇒ 45 + ∠b + 55 = 180°
⇒ ∠b + 100 = 180°
⇒ ∠b = 180° – 100°
⇒ ∠b = 80°

Question 13.
In the adjoining figure if x : y : z = 2 : 3 : 4, then find the value of z.

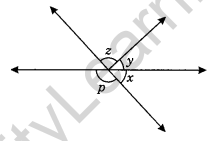
Solution:
Let x = 2s°
y = 3s°
and z = 4s°
∠x + ∠y + ∠z = 180° (Sum of adjacent angles on straight line)
2s° + 3s° + 4s° = 180°
⇒ 9s° = 180°
⇒ s° = 20°
Thus x = 2 × 20° = 40°, y = 3 × 20° = 60° and z = 4 × 20° = 80°

Question 14.
In the following figure, find the value of ∠BOC, if points A, O and B are collinear. (NCERT Exemplar)

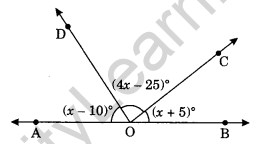
Solution:
We have A, O and B are collinear.
∠AOD + ∠DOC + ∠COB = 180° (Sum of adjacent angles on straight line)
(x – 10)° + (4x – 25)° + (x + 5)° = 180°
⇒ x – 10 + 4x – 25 + x + 5 = 180°
⇒ 6x – 10 – 25 + 5 = 180°
⇒ 6x – 30 = 180°
⇒ 6x = 180 + 30 = 210
⇒ x = 35
So, ∠BOC = (x + 5)° = (35 + 5)° = 40°

Question 15.
In given figure, PQ, RS and UT are parallel lines.
(i) If c = 57° and a = \(\frac { c }{ 3 }\), find the value of d.
(ii) If c = 75° and a = \(\frac { 2 }{ 5 }\)c , find b.

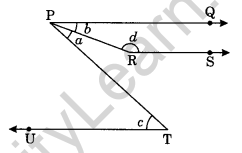
Solution:
(i) We have ∠c = 57° and ∠a = \(\frac { \angle c }{ 3 }\)
∠a = \(\frac { 57 }{ 3 }\) = 19°
PQ || UT (given)
∠a + ∠b = ∠c (Alternate interior angles)
19° + ∠b = 57°
∠b = 57° – 19° = 38°
PQ || RS (given)
∠b + ∠d = 180° (Co-interior angles)
38° + ∠d = 180°
∠d = 180° – 38° = 142°
Thus, ∠d = 142°
(ii) We have ∠c = 75° and ∠a = \(\frac { 2 }{ 5 }\) ∠c
∠a = \(\frac { 2 }{ 5 }\) × 75° = 30°
PQ || UT (given)
∠a + ∠b = ∠c
30° + ∠b = 75°
∠b = 75° – 30° = 45°
Thus, ∠b = 45°