CBSE Class 8 Maths Notes Chapter 12 Exponents and Powers
The numbers with negative exponents also obey the following laws:
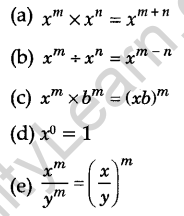
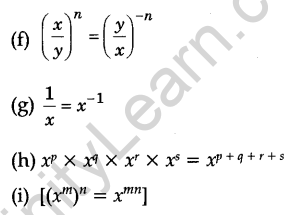
A number is said to be in the standard form, if it is expressed as the product of a number between 1 and 10 and the integral power of 10.
e.g., 149,600,000,000 = 1.496 × 1011
Very small numbers can be expressed in standard form using negative exponents.
e.g., 0.0016 = \(\frac { 16 }{ 10000 }\) = 1.6 × 10-3
If a is any non-zero integer and n is a positive integer, then a × a × a × …. × a (n times) is written as an,
i.e., an is the continued product of a multiplied by itself n times.
Here, ‘a’ is called the base and ‘n’ is called the ‘exponent’ or ‘index’. The number an is read as ‘a raised to the power of n’ or simply as ‘nth power of a’. The notation an is called the exponential notation or power notation.
We can write large numbers more conveniently using exponents.
For example:
10000 = 104; 243 = 35; 128 = 27, etc.
Now, we shall learn about negative exponents.
Powers With Negative Exponents
If a is any non-zero integer and m is a positive integer, then
\({ a }^{ -m }=\frac { 1 }{ { a }^{ m } }\)
Note: a-m is called the multiplicative inverse of am as a-m × am = 1.
It is obvious that am and a-m are multiplicative inverses of each other.
Laws of Exponents
If a, b are non-zero integers and m, n are any integers, then

Remember
- an = 1 ⇒ n = 0
- 1n = 1 where n is any integer.
- (-1)n = 1 where n is any even integer.
- (-1)n = -1 where n is any odd integer.
Use of Exponents to Express Small Numbers in Standard Form
A number is said to be in standard form if it can be expressed in the form K x 10n where 1 ≤ K < 10 and n is an integer.
A number written in standard form is said to be expressed in scientific notation.
Very small numbers can be expressed in standard form using negative exponents.
To express a large number, we move the decimal point to the left such that only one digit is left to the left side of the decimal point and multiply the resulting number by 10n where n is the number of places to which the decimal point has been moved to the left.
For example: 270,000,000,000 = 2.7 × 1011 (Decimal point has been moved to left for 11 places)
To express a number (<1), we move the decimal point to the right such that only one digit is left to the left side of the decimal point and multiply the resulting number by 10-n where n is the number of places to which the decimal point has been shifted to the right.
For example 0.0000009 = 9 × 10-7 (a Decimal point has been shifted to the right for 7 places.)
We hope the given CBSE Class 8 Maths Notes Chapter 12 Exponents and Powers Pdf free download will help you. If you have any query regarding NCERT Class 8 Maths Notes Chapter 12 Exponents and Powers, drop a comment below and we will get back to you at the earliest.





