Table of Contents
Squares and Square Roots Class 8 Extra Questions Maths Chapter 6
Extra Questions for Class 8 Maths Chapter 6 Squares and Square Roots
Squares and Square Roots Class 8 Extra Questions Very Short Answer Type
Question 1.
Find the perfect square numbers between 40 and 50.
Solution:
Perfect square numbers between 40 and 50 = 49.
Question 2.
Which of the following 242, 492, 772, 1312 or 1892 end with digit 1?
Solution:
Only 492, 1312 and 1892 end with digit 1.
Question 3.
Find the value of each of the following without calculating squares.
(i) 272 – 262
(ii) 1182 – 1172
Solution:
(i) 272 – 262 = 27 + 26 = 53
(ii) 1182 – 1172 = 118 + 117 = 235
Question 4.
Write each of the following numbers as difference of the square of two consecutive natural numbers.
(i) 49
(ii) 75
(iii) 125
Solution:
(i) 49 = 2 × 24 + 1
49 = 252 – 242
(ii) 75 = 2 × 37 + 1
75 = 382 – 372
(iii) 125 = 2 × 62 + 1
125 = 632 – 622
Question 5.
Write down the following as sum of odd numbers.
(i) 72
(ii) 92
Solution:
(i) 72 = Sum of first 7 odd numbers = 1 + 3 + 5 + 7 + 9 + 11 + 13
(ii) 92 = Sum of first 9 odd numbers = 1 + 3 + 5 + 7 + 9 + 11 + 13 + 15 + 17
Question 6.
Express the following as the sum of two consecutive integers.
(i) 152
(ii) 192
Solution:
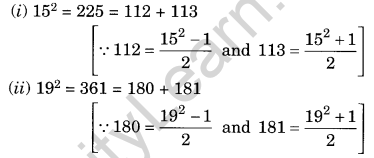
Question 7.
Find the product of the following:
(i) 23 × 25
(ii) 41 × 43
Solution:
(i) 23 × 25 = (24 – 1) (24 + 1) = 242 – 1 = 576 – 1 = 575
(ii) 41 × 43 = (42 – 1) (42 + 1) = 422 – 1 = 1764 – 1 = 1763
Question 8.
Find the squares of:
(i) \(\frac { -3 }{ 7 }\)
(ii) \(\frac { -9 }{ 17 }\)
Solution:
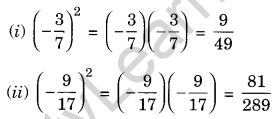
Question 9.
Check whether (6, 8, 10) is a Pythagorean triplet.
Solution:
2m, m2 – 1 and m2 + 1 represent the Pythagorean triplet.
Let 2m = 6 ⇒ m = 3
m2 – 1 = (3)2 – 1 = 9 – 1 = 8
and m2 + 1 = (3)2 + 1 = 9 + 1 = 10
Hence (6, 8, 10) is a Pythagorean triplet.
Alternative Method:
(6)2 + (8)2 = 36 + 64 = 100 = (10)2
⇒ (6, 8, 10) is a Pythagorean triplet.
Question 10.
Using property, find the value of the following:
(i) 192 – 182
(ii) 232 – 222
Solution:
(i) 192 – 182 = 19 + 18 = 37
(ii) 232 – 222 = 23 + 22 = 45
Squares and Square Roots Class 8 Extra Questions Short Answer Type
Question 11.
Using the prime factorisation method, find which of the following numbers are not perfect squares.
(i) 768
(ii) 1296
Solution:
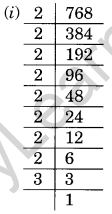
768 = 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2 × 3
Here, 3 is not in pair.
768 is not a perfect square.
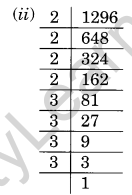
1296 = 2 × 2 × 2 × 2 × 3 × 3 × 3 × 3
Here, there is no number left to make a pair.
1296 is a perfect square.
Question 12.
Which of the following triplets are Pythagorean?
(i) (14, 48, 50)
(ii) (18, 79, 82)
Solution:
We know that 2m, m2 – 1 and m2 + 1 make Pythagorean triplets.
(i) For (14, 48, 50),
Put 2m =14 ⇒ m = 7
m2 – 1 = (7)2 – 1 = 49 – 1 = 48
m2 + 1 = (7)2 + 1 = 49 + 1 = 50
Hence (14, 48, 50) is a Pythagorean triplet.
(ii) For (18, 79, 82)
Put 2m = 18 ⇒ m = 9
m2 – 1 = (9)2 – 1 = 81 – 1 = 80
m2 + 1 = (9)2 + 1 = 81 + 1 = 82
Hence (18, 79, 82) is not a Pythagorean triplet.
Question 13.
Find the square root of the following using successive subtraction of odd numbers starting from 1.
(i) 169
(ii) 81
(iii) 225
Solution:
(i) 169 – 1 = 168, 168 – 3 = 165, 165 – 5 = 160, 160 – 7 = 153, 153 – 9 = 144, 144 – 11 = 133, 133 – 13 = 120, 120 – 15 = 105, 105 – 17 = 88, 88 – 19 = 69,
69 – 21 = 48, 48 – 23 = 25, 25 – 25 = 0
We have subtracted odd numbers 13 times to get 0.
√169 = 13
(ii) 81 – 1 = 80, 80 – 3 = 77, 77 – 5 = 72, 72 – 7 = 65, 65 – 9 = 56, 56 – 11 = 45, 45 – 13 = 32, 32 – 15 = 17, 17 – 17 = 0
We have subtracted 9 times to get 0.
√81 = 9
(iii) 225 – 1 = 224, 224 – 3 = 221, 221 – 5 = 216, 216 – 7 = 209, 209 – 9 = 200, 200 – 11 = 189, 189 – 13 = 176, 176 – 15 = 161, 161 – 17 = 144, 144 – 19 = 125,
125 – 21 = 104, 104 – 23 = 81, 81 – 25 = 56, 56 – 27 = 29, 29 – 29 = 0
We have subtracted 15 times to get 0.
√225 = 15
Question 14.
Find the square rootofthe following using prime factorisation
(i) 441
(ii) 2025
(iii) 7056
(iv) 4096
Solution:
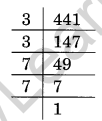
(i) 441 = 3 × 3 × 7 × 7
√441 = 3 × 7 = 21
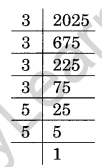
(ii) 2025 = 3 × 3 × 3 × 3 × 5 × 5
√2025 = 3 × 3 × 5 = 45
(iii) 7056 = 2 × 2 × 2 × 2 × 3 × 3 × 7 × 7
√7056 = 2 × 2 × 3 × 7 = 84

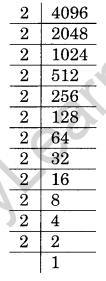
(iv) 4096 = 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2
√4096 = 2 × 2 × 2 × 2 × 2 × 2 = 64
Question 15.
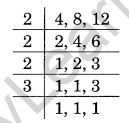
Find the least square number which is divisible by each of the number 4, 8 and 12.
Solution:
LCM of 4, 8, 12 is the least number divisible by each of them.
LCM of 4, 8 and 12 = 24
24 = 2 × 2 × 2 × 3
To make it perfect square multiply 24 by the product of unpaired numbers, i.e., 2 × 3 = 6
Required number = 24 × 6 = 144
Question 16.
Find the square roots of the following decimal numbers
(i) 1056.25
(ii) 10020.01
Solution:

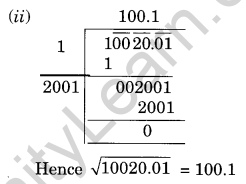
Question 17.
What is the least number that must be subtracted from 3793 so as to get a perfect square? Also, find the square root of the number so obtained.
Solution:
First, we find the square root of 3793 by division method.
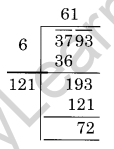
Here, we get a remainder 72
612 < 3793
Required perfect square number = 3793 – 72 = 3721 and √3721 = 61
Question 18.
Fill in the blanks:
(а) The perfect square number between 60 and 70 is …………
(b) The square root of 361 ends with digit …………..
(c) The sum of first n odd numbers is …………
(d) The number of digits in the square root of 4096 is ………..
(e) If (-3)2 = 9, then the square root of 9 is ……….
(f) Number of digits in the square root of 1002001 is …………
(g) Square root of \(\frac { 36 }{ 625 }\) is ………..
(h) The value of √(63 × 28) = …………
Solution:
(a) 64
(b) 9
(c) n2
(d) 2
(e) ±3
(f) 4
(g) \(\frac { 6 }{ 25 }\)
(h) 42
Question 19.
Simplify: √900 + √0.09 + √0.000009
Solution:
We know that √(ab) = √a × √b
√900 = √(9 × 100) = √9 × √100 = 3 × 10 = 30
√0.09 = √(0.3 × 0.3) = 0.3
√0.000009 = √(0.003 × 0.003) = 0.003
√900 + √0.09 + √0.000009 = 30 + 0.3 + 0.003 = 30.303
Squares and Square Roots Class 8 Extra Questions Higher Order Thinking Skills (HOTS)
Question 20.
Find the value of x if
\(\sqrt { 1369 } +\sqrt { 0.0615+x } =37.25\)
Solution:

Question 21.
Simplify:
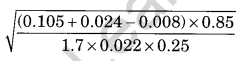
Solution:

Question 22.
A ladder 10 m long rests against a vertical wall. If the foot of the ladder is 6 m away from the wall and the ladder just reaches the top of the wall, how high is the wall? (NCERT Exemplar)
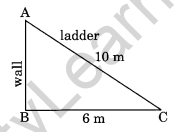
Solution:
Let AC be the ladder.
Therefore, AC = 10 m
Let BC be the distance between the foot of the ladder and the wall.
Therefore, BC = 6 m
∆ABC forms a right-angled triangle, right angled at B.
By Pythagoras theorem,
AC2 = AB2 + BC2
102 = AB2 + 62
or AB2 = 102 – 62 = 100 – 36 = 64
or AB = √64 = 8m
Hence, the wall is 8 m high.
Question 23.
Find the length of a diagonal of a rectangle with dimensions 20 m by 15 m. (NCERT Exemplar)
Solution:
Using Pythagoras theorem, we have Length of diagonal of the rectangle = \(\sqrt { { l }^{ 2 }+{ b }^{ 2 } }\) units
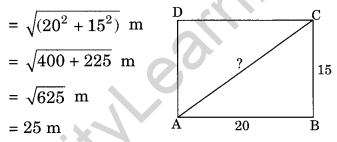
Hence, the length of the diagonal is 25 m.
Question 24.
The area of a rectangular field whose length is twice its breadth is 2450 m2. Find the perimeter of the field.
Solution:
Let the breadth of the field be x metres. The length of the field 2x metres.
Therefore, area of the rectangular field = length × breadth = (2x)(x) = (2x2) m2
Given that area is 2450 m2.
Therefore, 2x2 = 2450
⇒ x2 = 1225
⇒ x = √1225 or x = 35 m
Hence, breadth = 35 m
and length = 35 × 2 = 70 m
Perimeter of the field = 2 (l + b ) = 2(70 + 35) m = 2 × 105 m = 210 m.



































