To Measure the Dimensions of a Given Regular Body of Known Mass Using a Vernier Callipers and Hence Find its Density

To Measure the Dimensions of a Given Regular Body of Known Mass Using a Vernier Callipers and Hence Find its Density

Aim
To measure the dimensions of a given regular body of known mass using a Vernier Callipers and hence find its density.

Apparatus
Vernier callipers, a small rectangular metallic block or glass slab of known mass, magnifying lens.

Theory
(i) For measuring dimensions. Same as in Experiment 1 A.
(ii) For volume
Volume of a rectangular block = Length x Breadth x Thickness (height)
Density= Mass/Volume
i.e,.. ρ=m/V

Diagram

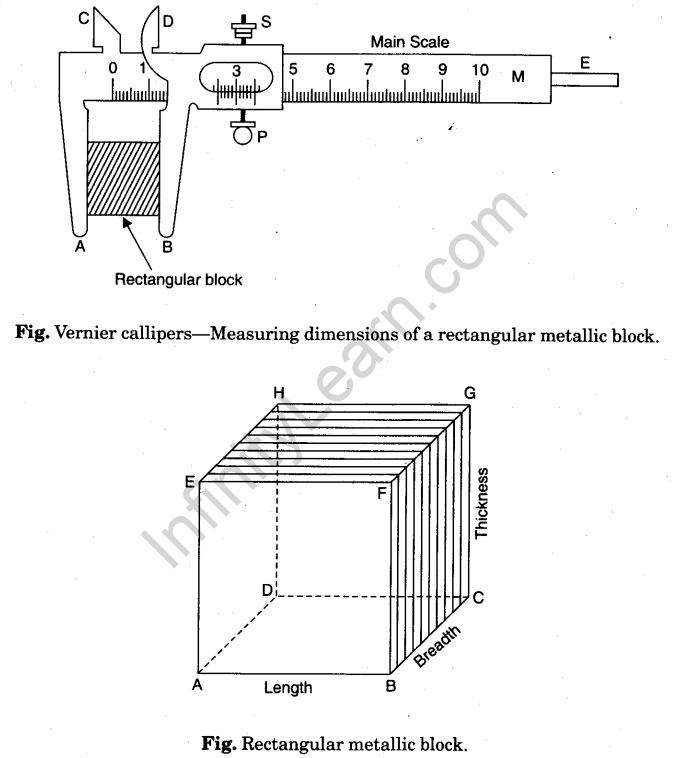
Procedure

1. Proceed in similar manner as in steps 1 to 5 in Experiment 1A.
2. Repeat above steps for the other edge of same face of same dimension.
3. Repeat above steps for other face of same dimension.
4. Repeat steps 1, 2 and 3 above for both edges of both faces of other dimensions.
5. Record your observations in tabular form.
6. Make calculations for each dimension applying zero correction.
7. Take mean of different values of same dimension.
8. Multiply the three mean dimensions to obtain volume of the block.
9. Calculate the density of the block material by dividing its known mass by obtained volume.

Observations

1. Known mass of the block, m =………..g.
2. Determination of Vernier Constant (Least Count) of the Vernier Callipers
   1 M.S.D. = 1 mm 10 V.S.D. = 9 M.S.D.
   ∴ 1 V.S.D. = 9/10 M.S.D. = 0.9 mm.
   Vernier constant, V.C. = 1 M.S.D. – 1 V.S.D. = (1 – 0.9) mm = 0.1 mm = 0.01 cm
3. Zero error = (i)…….cm, (ii)……… cm, (iii)………cm.
   Mean zero error (e) =……… cm
   Mean zero correction (c) = – e =………cm.
4. Table for the length (l)
   
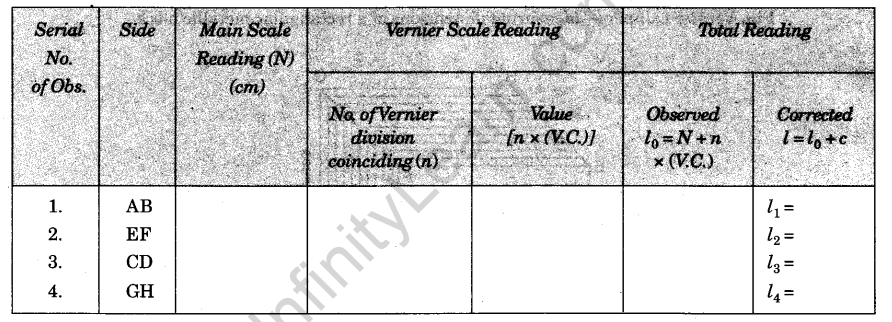
5. Table for the breadth (b)
   
6. Table for the thickness (t)
   

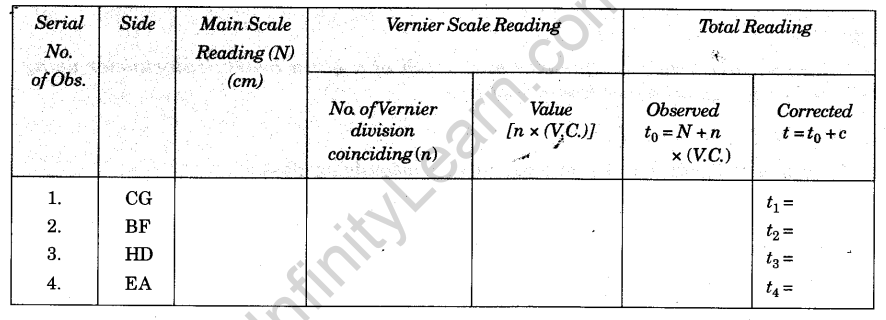
Calculations

Result
Density of block material = ………g cm^-3

Precautions
Same as given in Experiment 1A.

Sources of error
Same as given in Experiment 1A.