Table of Contents
Practical Work in Geography Class 11 Solutions Chapter 2 Map Scale
Class 11 Practical Work in Geography Chapter 2 NCERT Textbook Questions Solved
1. Choose the right answer from the four alternatives given below:
Question 1(i). Which one of the following methods of scale is a universal method?
(a) Simple Statement
(b) Representative Fraction
(c) Graphical Scale
(d) None of the above
Answer: (b) Representative fraction
Question 1(ii). Map distance in a scale is also known as:
(a) Numerator
(b) Denominator
(c) Statement of Scale
(d) Representative Fraction
Answer: (a) Numerator
Question 1(iii). ‘Numerator’ in scale represents:
(a) Ground distance
(b) Map distance
(c) Both the distances
(d) None of the above
Answer: (a) Ground Distance
2. Answer the following questions in about 30 words:
Question 2(i). What are the two different systems of measurement?
Answer: Kilometre, metre, centimetre etc. are used to measure the linear distances between two points on the ground. It is referred to as the Metric System of Measurement and presently used in India and many other countries of the world.
Another units which are used are miles, furlongs, yards, feet, etc. These are two different systems of measurement of the distances used in different countries of the world. It is known as the English System of Measurement and is prevalent in both the United
States and the United Kingdom. India also used this system for measuring/showing linear distances before 1957.
Question 2(ii). Give one example each of statement of scale in Metric and English system.
Answer: Metric System of Measurement
1 km = 1000 Metres
1 Metre = 100 Centimetres
1 Centimetre = 10 Millimetres
English System of Measurement
1 Mile = 8 Furlongs
1 Furlong = 220 Yards
1 Yard = 3 feet
1 Foot = 12 Inches.
Question 2(iii). Why is the Representative Fraction method called a Universal method?
Answer: Causes for the representative method being called universal:
- It shows the relationship between the map distance and the corresponding ground distance in units of length.
- The use of units to express the scale makes it the most versatile method.
- R. F. is generally shown in fraction because it shows how much the real world is reduced to fit on the map.
- For example, a fraction of 1 : 2,50,000 shows that one unit of length on the map represents 2,50,000 of the same units on the ground i.e. one mm, one cm or one inch on the map representing 2,50,000 mm, 2,50,000 cm and 2,50,000 inches, respectively of the ground.
- While converting the fraction of units into Metric or English systems, units in centimetre or inch are normally used by convention. This quality of expressing scale in units in R. F. makes it a universally acceptable and usable method.
Question 2(iv). What are the major advantages of the graphical method?
Answer: This type of scale shows map distances and the corresponding ground distances using a line bar with primary and secondary divisions marked on it. This is referred to as the graphical scale or bar scale.
Advantages:
- It can express scale not only in kilometres and metres but the readings may also be shown in miles and furlongs.
- Unlike the statement of the scale method, the graphical scale stands valid even when the map is reduced or enlarged. This is the unique advantage of the graphical method of the map scale.
3. Convert the given Statement of Scale into Representative Fraction (R. F.).
Question 3(i) 5 cm represents 10 km
Answer: Representative Fraction
![]()
Distance on Map = 5 cm
Distance on Ground = 10 km
Representative Fraction
= \(\frac{5}{10}\)
= \(\frac{1}{2}\) km or 2,00,000
Therefore representative fraction
= 1 : 2,00,000 cm
Question 3(ii). 2 inches represents 4 miles
Answer: Representative Fraction
![]()
2 inches = 4 miles
therefore, 1 inch = 2 miles (63,360 × 2)
1 inch on map = 1,26,720 inches on ground.
Therefore representative fraction
= 1:1,26, 720
Question 3(iii). 1 inch represents 1 yard
Answer: Representative Fraction
= \(\frac{1}{36}\)
Distance on Map = 1 inch
Distance on Ground = 1 yard
1 yard = 36 inches
Representative Fraction =
![]()
Therefore representative fraction = 1:36
Question 3(iv). 1 cm represents 100 metres
Answer: Representative Fraction
![]()
Distance on Map = 1 cm
Distance on Ground = 100 meters
1 cm = 100 meters
Representative Fraction =
= \(\frac{1}{10,000}\)
Therefore representative fraction
= 1 : 10,000
4. Convert the given Representative Fraction (R. F.) into Statement of Scale in the System of Measurement shown in parentheses:
Question 4(i). 1 : 100,000 (into km)
Answer: It means 1,00,000 cm on map represents 1 km on ground.
It means 1,00,000 centimetre on map represents 1,00,000 cm on ground.
Therefore, 1 cm represents 1 km
Question 4(ii). 1 : 31680 (into furlongs)
Answer: 1 inch represents 31,680 inches
1 mile = 8 furlongs
1 furlong = 220 yards
1 yard = 3 feet
1 foot = 12 inches
Therefore, 31680 inches = 31680 Divided by 12 x 3 x 220 furlongs = 4 furlongs
Therefore, 31680 inches = 4 furlongs
Question 4(iii). 1 : 126,720 (into miles)
Answer:
1 inch represents 1,26,720 inches
1 mile = 63,360 inches.
Therefore, 1,26,720 inches = 2 miles.
Hence, 1 inch represents 2 miles.
Question 4(iv). 1 : 50,000 (into metres)
Answer:
1 cm represents = 50,000 cm
1 metre = 100 cm
therefore, 1 cm represents 500 metres.
5. Construct a graphical scale when the given R. F. is 1 : 50,000 and read the distances in kilometre and metre.
Answer: According to a standard, generally, a length of 15 cm is taken to draw a graphical scale. 1:50,000 means that 1 cm on map shows 50,000 cm on ground. In other words, 1 cm shows 50,000 cm.
15 cm shows 50,000 x 15/1,00,000
15 cm = 7.5 km
Since 7.5 km is not an integer, so we can round it off to 5 or 10. Let us round it off to 5 km in this question.
Therefore, we need to make the following calculations to express the scale on a length of 5 km.
7.5 km is shown by 15 cm line.
Therefore, for 5 km we can express it as 15 x 5/7.5
0. 5 km will be shown by 1 cm on line.
We can make the graph by following steps:
First of all draw a 10 cm line and divide it in 5 important parts. Except for one part from the left, let us give all parts a distance of one km. Now divide the first part in 10 equal parts and each part will be equal to 100 metres. We can divide it in five parts as well and
taking one part as 200 metre and so on.

Class 11 Practical Work in Geography Chapter 2 NCERT Extra Questions
Class 11 Practical Work in Geography Chapter 2 Multiple Choice Questions
Question 1. Which of the following methods of scale remain unaffected on reducing the size of the map proportionally?
(а) By Scale Statement
(b) By representative Fraction
(c) By graphical or bar scale
(d) None of the above
Answer: (c) By graphical or bar scale
Question 2. Which of the following is an example of representative fraction?
(a) Centimetre
(b) Metre
(c) Inch
(d) None of the above
Answer: (d) None of the above
Question 3. When the scale of a map is expressed in a written statement, it is called:
(a) Statement of Scale
(b) Graphical Method
(c) Representative fraction
(d) Conversion of scale
Answer: (a) Statement of Scale
Question 4. Map distances and the corresponding ground distances using a line bar with primary and secondary divisions marked on it. This is referred to as what?
(a) Statement of Scale
(b) Graphical Method
(c) Representative fraction
(d) Conversion of scale
Answer: (b) Graphical Method
Question 5. When scale is represented as a ratio distance on map and distance on ground, it is called:
(a) Statement of Scale
(b) Graphical Method
(c) Representative fraction
(d) Conversion of scale
Answer: (c) Representative fraction
Question 6. What is the formula for representative Fraction?
Answer:

Answer:
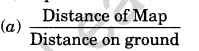
Class 11 Practical Work in Geography Chapter 2 Very Short Answer Type Questions
Question 1. What are different methods of showing scale on a map?
Answer: There are three methods of presenting scale:
- By scale statement
- by graphical or bar scale and
- by representative fraction.
Question 2. What is the scale?
Answer: The ratio between the distances of two points on the map, plan or photograph and the actual distance between the same two points on the ground is called scale.
Question 3. What is a representative fraction?
Answer: Representative Fraction is a method of scale of a map or plan expressed as a fraction showing the ratio between a unit distance on the map or plan, and the distance measured in the same units on the ground.
Question 4. What are advantages of representative fraction?
Answer: Representative fraction can be used in all countries whether we are acquainted with their unit system or not. Therefore, it is also called universal method of scale.
Question 5. Explain about the importance of scale.
Answer: A map scale provides the relationship between the map and the whole or a part of the earth’s surface shown on it. We can also express this relationship as a ratio of distances between two points on the map and the corresponding distance between the same two points on the ground.
Question 6. What is the unit in representative fraction?
Answer: There is no unit in representative fraction. It is only the ratio of distance on map and distance on ground.
| Related Links | |
| NCERT Solutions for Class 11 Maths | NCERT Solutions for Class 11 Biology |
| NCERT Solutions for Class 11 Physics | NCERT Solutions for Class 11 Chemistry |
Class 11 Practical Work in Geography Chapter 2 Short Answer Type Questions
Question 1. What is the utility of scale in a map?
Answer: A map scale provides the relationship between the map and the whole or a part of the earth’s surface shown on it. We can also express this relationship as a ratio of distances between two points on the map and the corresponding distance between the same two points on the ground.
- Scale of a map determines whether it can reflect minor details on it. For example to locate Palam Vihar in Gurgaon if we locate it on world map, it will be of no use. It is better to use a map of Gurgaon to locate Palam Vihar on it.
- On the basis of scale, maps are classified into small-scale maps and large-scale maps.
Question 2. What factors must be kept in mind while selecting scale?
Answer: We must consider following aspects while selecting scale:
- Purpose of map: If map is being drawn to study the minor details then we should make use of large scale maps and if it is to show physical features or large areas, we can use small scale maps as well. For example scale of a map of a house will be larger than
- map of a country.
- Space Available: Scale is also affected by availability of space for drawing maps.
Question 3.
Answer:
| Basis | Representative Fraction | Graphical Scale |
|
Meaning |
It is a method of scale of a map or plan expressed as a fraction showing the ratio between a unit distance on the map or plan, and the distance measured in the same units on the ground. | It shows map distances and the corresponding ground distances using a line bar with primary and secondary divisions marked on it. |
|
Impact |
It gets affected by changing the size of maps. | It is not affected by changing the size of maps proportionally. |
|
Unit |
It has no unit. | It has a unit. |
Question 4. What are limitations of representative fraction?
Answer: There are many limitations of representative fraction method. These are as follows:
- This method is only a fraction. It does not make use of any measurement system. Therefore it cannot be used to measure the direct distance between two places.
- Whenever maps are changed using computers, these fractions get changed.
- It is not easy to understand method for a layman.
Question 5. In a scale statement it is mentioned that 1 inch represents four miles. Express it in representative fraction.
Answer: 1 inch on map represents 4 miles on ground.
Or 1 inch = 4 x 63360 ( 1 mile = 63360 inches)
1 inch = 2,53,440 inches.
Therefore 1 inch on map represents a distance of 2,53,440 inches on ground. In other words, 1 unit on map represents 2,53,440 units on ground.
Therefore Representative fraction
![]()
Question 6. Convert Representative fraction 1:2,53,440 into a statement of scale (metric system).
Answer: The given representative fraction can be converted into statement of scale in following steps:
1: 2,53,440 means that 1 unit on map represents 2,53,440 units on the ground. In other words, 1 cm will represent 2,53,440/1,00,000 km (because 1 km = 1,00,000 cm)
Therefore, 1 cm = 2.5344 km In statement of scale form we can say that 1 cm represents 2.5344 km.
Class 11 Practical Work in Geography Chapter 2 Long Answer Type Questions
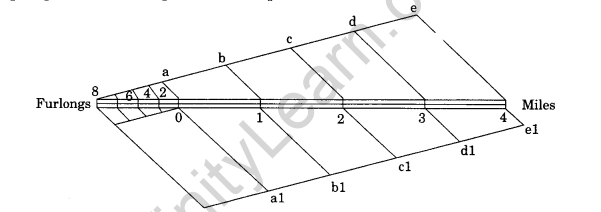
Question 1. Construct a graphical scale for representative fraction 1:50,000 in which distance is given in furlongs and miles.
Answer: For graphical scale, to know the length of the line we need to make following calculations. 1:50,000 means 1 unit on map represents 50,000 units on ground.
In this way, 1 inch = 50,000 inches
6 inches = 50,000 x 6/63360
6 inches = 4.73 miles
Since 4.73 miles is not an integer, therefore we take 5 as an integer on number line. Now we need to make following calculations to present number line as 5 miles.
Since 6 inches = 4.73 miles
Therefore 5 miles = 6 x 5/4.73
5 miles will be represented by 6.34 inches.
We can make the graph by following steps:
First of all draw a 6.34 inches line and divide it in 5 important parts. Except one part from the left, let us give all parts a distance of 1.268 inch. Now divide the first part in 4 equal parts and each part will be equal to 0.32 inch.
Question 2. Construct a graphical scale for scale 1 inch = 1 mile and which can be read in furlongs and miles.
Answer: For graphical scale, to know the length of the line we need to make following calculations.
1 inch = 1 mile
Since 1 inch = 1 mile and therefore, 6 inches = 6 miles We can make the graph by following steps:
First of all draw a 6 inches line and divide it in 6 important parts. Except one part from the left, let us give all parts a distance of one 1 inch. Now divide the first part in 4 equal parts and each part will be equal to 0.25 inch.

Class 11 Practical Work in Geography Chapter 2 Viva Questions
Question 1. According to English System of Measurement, convert 1 Mile into furlongs, yards, feet and inches.
Answer:
1 mile = 8 Furlongs = 1720 yards = 5280 feet
1 Furlong = 220 Yards = 660 feet = 7920 inches
1 Yard = 3 feet = =36 inch
1 Foot = 12 Inches
Question 2. Give formula for representative fraction.
Answer: Representative fraction is equal to distance on map divided by distance on ground.
Question 3. If less space is available, what kind of scale will you choose?
Answer: Large Scale
Question 4. If you wish to study minor details of a map what kind of scale will you choose?
Answer: Small Scale
Question 5.What are different methods of showing scale on a map?
Answer: There are three methods of presenting scale:
- By scale statement;
- by graphical or bar scale and
- by representative fraction.
Question 6. What is the unit in representative fraction?
Answer: There is no unit in representative fraction.
Map Scale Notes
- A map scale provides the relationship between the map and the whole or a part of the earth’s surface shown on it. We can also express this relationship as a ratio of distances between two points on the map and the corresponding distance between the same
- two points on the ground.
- There are three methods of presenting scale:
- By scale statement;
- by graphical or bar scale and
- by representative fraction.
- Kilometre, metre, centimetre etc. are used to measure the linear distances between two points on the ground. It is referred to as the Metric System of Measurement and presently used in India and many other countries of the world.
- Metric System of Measurement 1 km = 1000 Metres 1 Metre = 100 Centimetres 1 Centimetre = 10 Millimetres
- Another units which are used are miles, furlongs, yards, feet, etc. These are two different systems of measurement of the distances used in different countries of the world. It is known as the English System of Measurement and is prevalent in both the United
- States and the United Kingdom. India also used this system for measuring/showing linear distances before 1957.
- English System of Measurement
- 1 Mile = 8 Furlongs
- 1 Furlong = 220 Yards
- 1 Yard = 3 feet
- 1 Foot = 12 Inches

Map Scale Important Terms
- Denominator: The number below the line in a fraction is called denominator. For example, in a fraction of 1 : 20,000, 20,000 is the denominator.
- Numerator: The number above the line in a fraction is called numerator. For example, in a fraction of 1 : 20,000, 1 is the numerator.
- Representative Fraction: It is a method of scale of a map or plan expressed as a fraction showing the ratio between a unit distance on the map or plan, and the distance measured in the same units on the ground.
- Statement of Scale: The scale of a map may be indicated in the form of a written statement. For example, if on a map a written statement appears stating 1 cm represents 10 km, it means that on that map a distance of 1 cm is representing 10 km of the
- corresponding ground distance.
- Graphical or Bar Scale: It shows map distances and the corresponding ground distances using a line bar with primary and secondary divisions marked on it. This is referred to as the graphical scale or bar scale.
- Scale: The ratio between the distances of two points on the map, plan or photograph and the actual distance between the same two points on the ground is called scale.









