NCERT Notes – Class 9 Maths Chapter 2 Polynomials

NCERT Notes – Class 9 Maths

Get NCERT Notes for Class 9 Maths on Infinity Learn for free.

 

Chapter 2 – Polynomials

1. Polynomial: A polynomial in one variable x is an algebraic expression of the form

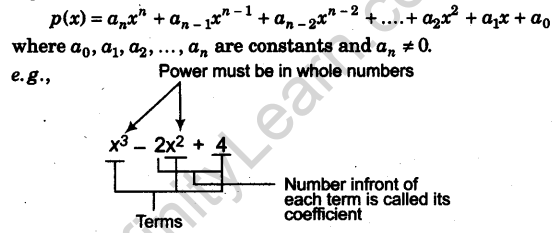
2. Terms: The terms of the expression are the components of a polynomial that are separated by ‘+’ or ‘-‘ operations.

3. Types of Polynomial
(i) Constant polynomial: A constant polynomial is a polynomial that has only one term, which is a constant.
e.g., -6, 4, \(\frac { 2 }{ 3 }\), \(\frac { -3 }{ 4 }\) etc., are still constant polynomial.
Generally, each real number is a constant polynomial.

(ii) Zero polynomial: A zero polynomial is a polynomial that only has one term, which is zero.

(iii) Monomial: Monomials are polynomials that have only one term. (‘mono’ means ‘one’).
e.g., µ⁴³, \(\frac { 7 }{ 3 }\) xz and – 2 are all monomials.

(iv) Binomial:Binomials are polynomials with only two terms. (‘bi’ means ‘two’).
e.g., (x² + x), (y³⁰ + √2) and (5x²y + 6xz) are all binomials.

(v) Trinomial: Trinomials are polynomials with only three terms. (‘tri’ means ‘three’).
e.g., (x⁴ + x³ + √2), (µ⁴³ + µ⁷ + µ) and (8y – 5xy + 9xy²) are all trinomials.

4. The degree of a Polynomial: The degree of a polynomial is the highest power of the variable in the polynomial.

(a) In one variable: The highest power of the variable in the case of a polynomial in one variable is called the polynomial’s degree.
e.g.,
√2 – y³ + y⁵ + 2y⁶ is a polynomial in y of degree 6.
6x + √3 is a polynomial in x of degree 1.

(b) In two or more variables: The sum of the powers of the variables in each term is taken up in the case of a polynomial in more than one variable, and the largest sum thus achieved is called the polynomial’s degree.
e.g.,
3x³ – 7x²y² + 8 is a polynomial in x and y of degree 4.
8a⁸b – 4ab + √2 is a polynomial in a and b of degree 9.

Note:
The degree of a non-zero constant polynomial is ‘zero’.
The degree of a zero polynomial is not defined.

5. Linear Polynomial: A linear polynomial is a polynomial with degree one.
e.g.,
x + √7 is a linear polynomial in x, y and z.
√2 µ + 3 is a linear polynomial in µ.

6. Quadratic Polynomial: A quadratic polynomial is a polynomial with degree two.
e.g;
xy + yz + zx is a quadratic polynomial in x, y and z.
x² + 9x – \(\frac { 3 }{ 2 }\) is a quadratic polynomial in x.

7. Cubic Polynomial: A cubic polynomial is a polynomial of degree three.
e.g.,
ax³ + bx² + cx + d is a cubic polynomial in x and a, b, c, d are constants.
2y³ + 3 is a cubic polynomial in y.
9x²y + xy – 4 is a cubic polynomial in x and y.

8. Value of a Polynomial: Value of a polynomial p(x) at x = a is p(a).
e.g., If p(x) = x² + 2x + 6 then, at x = 2, p(2) = 2² + 2 × 2 + 6 = 14

9. Zeroes of a Polynomial: Zeroes of a polynomial p(x) is a number a such that p(a) = 0.

• A polynomial’s zero can be zero.
• There is only one zero in every linear polynomial.
• The root of a polynomial is the zero of the polynomial.
• There is no zero in a non-zero constant polynomial.
• A zero of the zero polynomial is any real number.
• There can be more than one zero in a polynomial.

A polynomial’s maximum number of zeroes is equal to its degree.

10. Remainder Theorem: Let p (x) be any polynomial of degree n greater than or equal to one (n ≥ 1) and let a be any real number. If p (x) is divided by the linear polynomial x – a, then the remainder is p (a).
Dividend = (Divisor × Quotient) + Remainder

11. Factor Theorem: Let q(x) be a polynomial of degree n ≥ 1 and a be any real number, then
(i) (x – a) is a factor of q (x), if q(a) = 0 and
(ii) q(a) = 0, if x – a is a factor of q (x).

12. The factorisation of Quadratic Polynomials
(i) By splitting the middle term: Suppose a quadratic polynomial is x² + lx + m where l and m are constants.
Now, we split the middle term lx as ax + bx, so that ab = m. Then,
x² + lx + m = x² + ax + bx + ab = x(x + a) + b(x + a) = (x + a) (x + b)

(ii) By using factor theorem: Suppose, ax² + bx + c be a quadratic polynomial. Let two factors be (x – α) and (x – β)
∴ a (x – α) (x – β) = ax² + bx + c
⇒ ax² – a(α + β)x + aαβ = ax² + bx + c
On equating the coefficient of x and constant term.
We get, α + β = \(\frac { -b }{ a }\) and αβ = \(\frac { c }{ a }\)
On simplifying, we get the values of α and β.

(iii) The factorisation of cubic polynomials: For cubic polynomials, the dividing middle term approach is not applicable. It must first discover at least one factor, after which it must adjust the given polynomial so that it becomes the product of two terms, one of which is that factor and the other a quadratic polynomial. Now use the previous procedure to solve this quadratic polynomial.

13. Algebraic Identities: An algebraic identity is an algebraic equation that holds true for all possible values of the variable.
The following are some algebraic identities.

• (x + y)² = x² + 2xy + y²
• (x – y)² = x² – 2xy + y²
• x² – y² = (x + y)(x – y)
• (x + a)(x + b)= x² + (a + b)x + ab
• (x + y + z)² = x² + y² + z² + 2xy + 2yz + 2zx
• (x + y)³ = x³ + y³ + 3xy(x + y)
• (x – y)³ = x³ – y³ – 3xy(x – y)
• x³ + y³ + z³ – 3xyz = (x + y + z)(x² + y² + z² – xy – yz – zx)
  If x + y + z = 0, then x³ + y³ + z³ = 3xyz