Direction Cosines of a Line: If the directed line OP makes angles α, β, and γ with positive X-axis, Y-axis and Z-axis respectively, then cos α, cos β, and cos γ, are called direction cosines of a line. They are denoted by l, m, and n. Therefore, l = cos α, m = cos β and n = cos γ. Also, sum of squares of direction cosines of a line is always 1,
i.e. l2 + m2 + n2 = 1 or cos2 α + cos2 β + cos 2 γ = 1
Note: Direction cosines of a directed line are unique.
Direction Ratios of a Line: Number proportional to the direction cosines of a line, are called direction ratios of a line.
(i) If a, b and c are direction ratios of a line, then \(\frac { l }{ a }\) = \(\frac { m }{ b }\) = \(\frac { n }{ c }\)
(ii) If a, b and care direction ratios of a line, then its direction cosines are
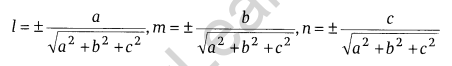
(iii) Direction ratios of a line PQ passing through the points P(x1, y1, z1) and Q(x2, y2, z2) are x2 – x1, y2 – y1 and z2 – z1 and direction cosines are
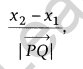
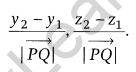
Note:
(i) Direction ratios of two parallel lines are proportional.
(ii) Direction ratios of a line are not unique.
Straight line: A straight line is a curve, such that all the points on the line segment joining any two points of it lies on it.
Equation of a Line through a Given Point and parallel to a given vector \(\vec { b }\)
Vector form \(\vec { r } =\vec { a } +\lambda \vec { b }\)
where, \(\vec { a }\) = Position vector of a point through which the line is passing
\(\vec { b }\) = A vector parallel to a given line
Cartesian form
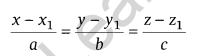
where, (x1, y1, z1) is the point through which the line is passing through and a, b, c are the direction ratios of the line.
If l, m, and n are the direction cosines of the line, then the equation of the line is
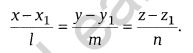
Remember point: Before we use the DR’s of a line, first we have to ensure that coefficients of x, y and z are unity with a positive sign.
Equation of Line Passing through Two Given Points
Vector form: \(\vec { r } =\vec { a } +\lambda \left( \vec { b } -\vec { a } \right)\), λ ∈ R, where a and b are the position vectors of the points through which the line is passing.
Cartesian form
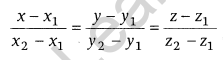
where, (x1, y1, z1) and (x2, y2, z2) are the points through which the line is passing.
Angle between Two Lines
Vector form: Angle between the lines \(\vec { r } =\vec { { a }_{ 1 } } +\lambda \vec { { b }_{ 1 } }\) and \(\vec { r } =\vec { { a }_{ 2 } } +\mu \vec { { b }_{ 2 } }\) is given as
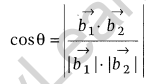

Condition of Perpendicularity: Two lines are said to be perpendicular, when in vector form \(\vec { { b }_{ 1 } } \cdot \vec { { b }_{ 2 } } =0\); in cartesian form a1a2 + b1b2 + c1c2 = 0
or l1l2 + m1m2 + n1n2 = 0 [direction cosine form]
Condition that Two Lines are Parallel: Two lines are parallel, when in vector form \(\vec { { b }_{ 1 } } \cdot \vec { { b }_{ 2 } } =\left| \vec { { b }_{ 1 } } \right| \left| \vec { { b }_{ 2 } } \right|\); in cartesian form \(\frac { { a }_{ 1 } }{ { a }_{ 2 } } =\frac { { b }_{ 1 } }{ { b }_{ 2 } } =\frac { { c }_{ 1 } }{ { c }_{ 2 } }\)
or
\(\frac { { l }_{ 1 } }{ { l }_{ 2 } } =\frac { { m }_{ 1 } }{ { m }_{ 2 } } =\frac { { n }_{ 1 } }{ { n }_{ 2 } }\)
[direction cosine form]
Shortest Distance between Two Lines: Two non-parallel and non-intersecting straight lines, are called skew lines.
For skew lines, the line of the shortest distance will be perpendicular to both the lines.
Vector form: If the lines are \(\vec { r } =\vec { { a }_{ 1 } } +\lambda \vec { { b }_{ 1 } }\) and \(\vec { r } =\vec { { a }_{ 2 } } +\lambda \vec { { b }_{ 2 } }\). Then, shortest distance
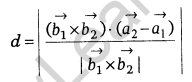
where \(\vec { { a }_{ 2 } }\), \(\vec { { a }_{ 1 } }\) are position vectors of point through which the line is passing and \(\vec { { b }_{ 1 } }\), \(\vec { { b }_{ 2 } }\) are the vectors in the direction of a line.
Cartesian form: If the lines are
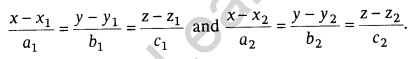
Then, shortest distance,
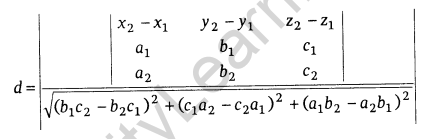
Distance between two Parallel Lines: If two lines l1 and l2 are parallel, then they are coplanar. Let the lines be \(\vec { r } =\vec { { a }_{ 1 } } +\lambda \vec { b }\) and \(\vec { r } =\vec { { a }_{ 2 } } +\mu \vec { b }\), then the distance between parallel lines is
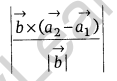
Note: If two lines are parallel, then they both have same DR’s.
Distance between Two Points: The distance between two points P (x1, y1, z1) and Q (x2, y2, z2) is given by
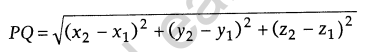
Mid-point of a Line: The mid-point of a line joining points A (x1, y1, z1) and B (x2, y2, z2) is given by
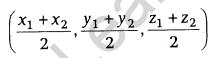
Plane: A plane is a surface such that a line segment joining any two points of it lies wholly on it. A straight line which is perpendicular to every line lying on a plane is called a normal to the plane.
Equations of a Plane in Normal form
Vector form: The equation of plane in normal form is given by \(\vec { r } \cdot \vec { n } =d\), where \(\vec { n }\) is a vector which is normal to the plane.
Cartesian form: The equation of the plane is given by ax + by + cz = d, where a, b and c are the direction ratios of plane and d is the distance of the plane from origin.
Another equation of the plane is lx + my + nz = p, where l, m, and n are direction cosines of the perpendicular from origin and p is a distance of a plane from origin.
Note: If d is the distance from the origin and l, m and n are the direction cosines of the normal to the plane through the origin, then the foot of the perpendicular is (ld, md, nd).
Equation of a Plane Perpendicular to a given Vector and Passing Through a given Point
Vector form: Let a plane passes through a point A with position vector \(\vec { a }\) and perpendicular to the vector \(\vec { n }\), then \(\left( \vec { r } -\vec { a } \right) \cdot \vec { n } =0\)
This is the vector equation of the plane.
Cartesian form: Equation of plane passing through point (x1, y1, z1) is given by
a (x – x1) + b (y – y1) + c (z – z1) = 0 where, a, b and c are the direction ratios of normal to the plane.
Equation of Plane Passing through Three Non-collinear Points
Vector form: If \(\vec { a }\), \(\vec { b }\) and \(\vec { c }\) are the position vectors of three given points, then equation of a plane passing through three non-collinear points is \(\left( \vec { r } -\vec { a } \right) \cdot \left\{ \left( \vec { b } -\vec { a } \right) \times \left( \vec { c } -\vec { a } \right) \right\} =0\).
Cartesian form: If (x1, y1, z1) (x2, y2, z2) and (x3, y3, z3) are three non-collinear points, then equation of the plane is
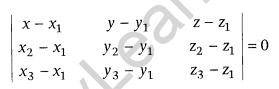
If above points are collinear, then
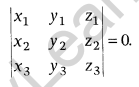
Equation of Plane in Intercept Form: If a, b and c are x-intercept, y-intercept and z-intercept, respectively made by the plane on the coordinate axes, then equation of plane is \(\frac { x }{ a } +\frac { y }{ b } +\frac { z }{ c } =1\)
Equation of Plane Passing through the Line of Intersection of two given Planes
Vector form: If equation of the planes are \(\vec { r } \cdot \vec { { n }_{ 1 } } ={ d }_{ 1 }\) and \(\vec { r } \cdot \vec { { n }_{ 2 } } ={ d }_{ 2 }\), then equation of any plane passing through the intersection of planes is
\(\vec { r } \cdot \left( \vec { { n }_{ 1 } } +\lambda \vec { { n }_{ 2 } } \right) ={ d }_{ 1 }+\lambda { d }_{ 2 }\)
where, λ is a constant and calculated from given condition.
Cartesian form: If the equation of planes are a1x + b1y + c1z = d1 and a2x + b2y + c2z = d2, then equation of any plane passing through the intersection of planes is a1x + b1y + c1z – d1 + λ (a2x + b2y + c2z – d2) = 0
where, λ is a constant and calculated from given condition.
Coplanarity of Two Lines
Vector form: If two lines \(\vec { r } =\vec { { a }_{ 1 } } +\lambda \vec { { b }_{ 1 } }\) and \(\vec { r } =\vec { { a }_{ 2 } } +\mu \vec { { b }_{ 2 } }\) are coplanar, then
\(\left( \vec { { a }_{ 2 } } -\vec { { a }_{ 1 } } \right) \cdot \left( \vec { { b }_{ 2 } } -\vec { { b }_{ 1 } } \right) =0\)
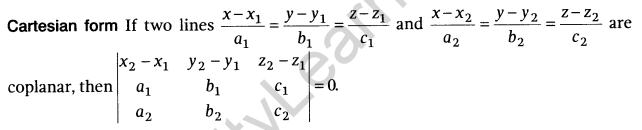
Angle between Two Planes: Let θ be the angle between two planes.
Vector form: If \(\vec { { n }_{ 1 } }\) and \(\vec { { n }_{ 2 } }\) are normals to the planes and θ be the angle between the planes \(\vec { r } \cdot \vec { { n }_{ 1 } } ={ d }_{ 1 }\) and \(\vec { r } \cdot \vec { { n }_{ 2 } } ={ d }_{ 2 }\), then θ is the angle between the normals to the planes drawn from some common points.
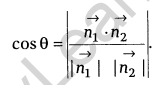
Note: The planes are perpendicular to each other, if \(\vec { { n }_{ 1 } } \cdot \vec { { n }_{ 2 } } =0\) and parallel, if \(\vec { { n }_{ 1 } } \cdot \vec { { n }_{ 2 } } =\left| \vec { { n }_{ 1 } } \right| \left| \vec { { n }_{ 2 } } \right|\)
Cartesian form: If the two planes are a1x + b1y + c1z = d1 and a2x + b2y + c2z = d2, then
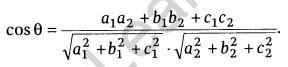
Note: Planes are perpendicular to each other, if a1a2 + b1b2 + c1c2 = 0 and planes are parallel, if \(\frac { { a }_{ 1 } }{ { a }_{ 2 } } =\frac { { b }_{ 1 } }{ { b }_{ 2 } } =\frac { { c }_{ 1 } }{ { c }_{ 2 } }\)
Distance of a Point from a Plane
Vector form: The distance of a point whose position vector is \(\vec { a }\) from the plane
\(\vec { r } \cdot \hat { n } =d\quad is\quad \left| d-\vec { a } \hat { n } \right|\)
Note:
(i) If the equation of the plane is in the form \(\vec { r } \cdot \vec { n } =d\), where \(\vec { n }\) is normal to the plane, then the perpendicular distance is \(\frac { \left| \vec { a } \cdot \vec { n } -d \right| }{ \left| \vec { n } \right| }\)
(ii) The length of the perpendicular from origin O to the plane \(\vec { r } \cdot \vec { n } =d\quad is\quad \frac { \left| d \right| }{ \left| \vec { n } \right| }\) [∵ \(\vec { a }\) = 0]
Cartesian form: The distance of the point (x1, y1, z1) from the plane Ax + By + Cz = D is
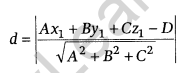
Angle between a Line and a Plane
Vector form: If the equation of line is \(\vec { r } =\vec { a } +\lambda \vec { b }\) and the equation of plane is \(\vec { r } \cdot \vec { n } =d\), then the angle θ between the line and the normal to the plane is
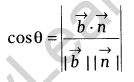
and so the angle Φ between the line and the plane is given by 90° – θ,
i.e. sin(90° – θ) = cos θ
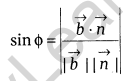
Cartesian form: If a, b and c are the DR’s of line and lx + my + nz + d = 0 be the equation of plane, then
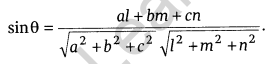
If a line is parallel to the plane, then al + bm + cn = 0 and if line is perpendicular to the plane, then \(\frac { a }{ l } =\frac { b }{ m } =\frac { c }{ n }\)
Remember Points
(i) If a line is parallel to the plane, then normal to the plane is perpendicular to the line. i.e. a1a2 + b1b2 + c1c2 = 0
(ii) If a line is perpendicular to the plane, then DR’s of line are proportional to the normal of the plane.
i.e. \(\frac { { a }_{ 1 } }{ { a }_{ 2 } } =\frac { { b }_{ 1 } }{ { b }_{ 2 } } =\frac { { c }_{ 1 } }{ { c }_{ 2 } }\)
where, a1, b1 and c1 are the DR’s of a line and a2, b2 and c2 are the DR’s of normal to the plane.


