Matrix: A matrix is an ordered rectangular array of numbers or functions. The numbers or functions are called the elements or the entries of the matrix.
Order of a Matrix: If a matrix has m rows and n columns, then its order is written as m × n. If a matrix has order m × n, then it has mn elements.
In general, am×n matrix has the following rectangular array:
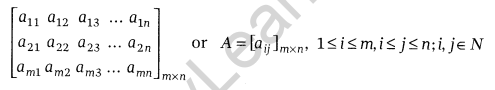
Note: We shall consider only those matrices, whose elements are real numbers or functions taking real values.
Types of Matrices
Column Matrix: A matrix which has only one column, is called a column matrix.
e.g. \(\left[ \begin{matrix} 1 \\ 0 \\ -5 \end{matrix} \right]\)
In general, A = [aij]m×1 is a column matrix of order m × 1.
Row Matrix: A matrix which has only one row, is called a row matrix,
e.g. \(\left[ \begin{matrix} 1 & 5 & 9 \end{matrix} \right]\)
In general, A = [aij]1×n is a row matrix of order 1 x n
Square Matrix: A matrix which has equal number of rows and columns, is called a square matrix
e.g. \(\begin{bmatrix} 3 & -1 \\ 5 & 2 \end{bmatrix}\)
In general, A = [aij]m x m is a square matrix of order m.
Note: If A = [aij] is a square matrix of order n, then elements a11, a22, a33,…, ann is said to constitute the diagonal of the matrix A.
Diagonal Matrix: A square matrix whose all the elements except the diagonal elements are zeroes, is called a diagonal matrix,
e.g. \(\left[ \begin{matrix} 3 & 0 & 0 \\ 0 & -3 & 0 \\ 0 & 0 & -8 \end{matrix} \right]\)
In general, A = [aij]m×m is a diagonal matrix, if aij = 0, when i ≠ j.
Scalar Matrix: A diagonal matrix whose all diagonal elements are same (non-zero), is called a scalar matrix,
e.g. \(\left[ \begin{matrix} 2 & 0 & 0 \\ 0 & 2 & 0 \\ 0 & 0 & 2 \end{matrix} \right]\)
In general, A = [aij]n×n is a scalar matrix, if aij = 0, when i ≠ j, aij = k (constant), when i = j.
Note: A scalar matrix is a diagonal matrix but a diagonal matrix may or may not be a scalar matrix.
Unit or Identity Matrix: A diagonal matrix in which all diagonal elements are ‘1’ and all non-diagonal elements are zero, is called an identity matrix. It is denoted by I.
e.g. \(\left[ \begin{matrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{matrix} \right]\)
In general, A = [aij]n×n is an identity matrix, if aij = 1, when i = j and aij = 0, when i ≠ j.
Zero or Null Matrix: A matrix is said to be a zero or null matrix, if its all elements are zer0
e.g. \(\begin{bmatrix} 0 & 0 \\ 0 & 0 \end{bmatrix}\)
Equality of Matrices: Two matrices A and B are said to be equal, if
(i) order of A and B are same.
(ii) corresponding elements of A and B are same i.e. aij = bij, ∀ i and j.
e.g. \(\begin{bmatrix} 2 & 1 \\ 0 & 3 \end{bmatrix}\) and \(\begin{bmatrix} 2 & 1 \\ 0 & 3 \end{bmatrix}\) are equal matrices, but \(\begin{bmatrix} 3 & 2 \\ 0 & 1 \end{bmatrix}\) and \(\begin{bmatrix} 2 & 3 \\ 0 & 1 \end{bmatrix}\) are not equal matrices.
Operations on Matrices
Between two or more than two matrices, the following operations are defined below:
Addition and Subtraction of Matrices: Addition and subtraction of two matrices are defined in an order of both the matrices are same.
Addition of Matrix
If A = [aij]m×n and B = [yij]m×n, then A + B = [aij +bij]m×n, 1 ≤ i ≤ m, 1 ≤ j ≤ n
Subtraction of Matrix
If A = [aij]m×n and B = [bij]m×n, then A – B = [aij – bij]m×n, 1 ≤ i ≤ m, 1 ≤ j ≤ n
Properties of Addition of Matrices
(a) Commutative If A = [aij] and B = [bij] are matrices of the same order say m x n then A + B = B + A,
(b) Associative for any three matrices A = [aij], B = [bij], C = [cij] of the same order say m x n, A + (B + C) = (A + B) + C.
(c) Existence of additive identity Let A = [aij] be amxn matrix and O be amxn zero matrix, then A + O = O + A = A. In other words, O is the additive identity for matrix addition.
(d) Existence of additive inverse Let A = [aij]m×n be any matrix, then we have another matrix as -A = [-aij]m×n such that A + (-A) = (-A + A) = O. So, matrix (-A) is called additive inverse of A or negative of A.
Note
(i) If A and B are not of the same order, then A + B is not defined.
(ii) Addition of matrices is an example of a binary operation on the set of matrices of the same order.
Multiplication of a matrix by scalar number: Let A = [aij]m×n be a matrix and k is scalar, then kA is another matrix obtained by multiplying each element of A by the scalar k, i.e. if A = [aij]m×n, then kA = [kaij]m×n.
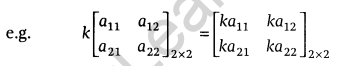
Properties of Scalar Multiplication of a Matrix
Let A = [aij] and B = [bij]be two matrices of the same order say m × n, then
(a) k(A + B) = kA + kB, where k is a scalar.
(b) (k + l)A = kA + lA, where k and l are scalars.
Multiplication of Matrices: Let A and B be two matrices. Then, their product AB is defined, if the number of columns in matrix A is equal to the number of rows in matrix B.

Properties of Multiplication of Matrices
(a) Non-commutativity Matrix multiplication is not commutative i.e. if AB and BA are both defined, then it is not necessary that AB ≠ BA.
(b) Associative law For three matrices A, B, and C, if multiplication is defined, then A (BC) = (AB) C.
(c) Multiplicative identity For every square matrix A, there exists an identity matrix of the same order such that IA = AI = A.
Note: For Amxm, there is only one multiplicative identity Im.
(d) Distributive law For three matrices A, B, and C,
A(B + C) = AB + AC
(A + B)C = AC + BC
whenever both sides of the equality are defined.
Note: If A and B are two non-zero matrices, then their product may be a zero matrix.
e.g. Suppose A = \(\begin{bmatrix} 0 & -1 \\ 0 & 2 \end{bmatrix}\) and B = \(\begin{bmatrix} 3 & 5 \\ 0 & 0 \end{bmatrix}\), then AB = \(\begin{bmatrix} 0 & 0 \\ 0 & 0 \end{bmatrix}\).



