Volume Formulae
Volume is a measure of the amount of space occupied by a three-dimensional object. The formulas for calculating volume vary depending on the shape of the object. Here are some common volume formulas for different shapes:
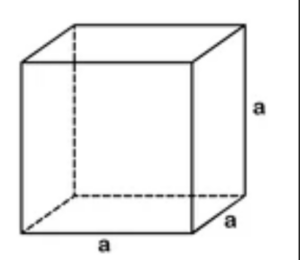
Volume of Cube:
The volume of a cube is given by the formula,
V = side³,
Where “side” represents the length of one side of the cube.
Volume of the following cube = a3
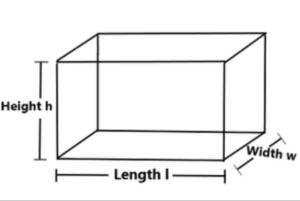
Volume of Rectangular Prism OR Cuboid:
The volume of a rectangular prism is calculated using the formula,
V = length × width × height,
Where “length,” “width,” and “height” represent the dimensions of the prism.
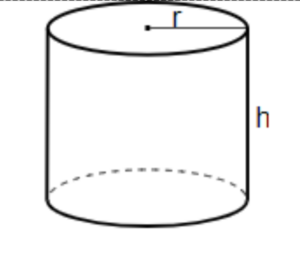
Volume of Cylinder:
The volume of a cylinder is determined by the formula,
V = π × radius² × height,
Where “radius” is the distance from the centre of the base to its edge, and “height” is the perpendicular distance between the bases.
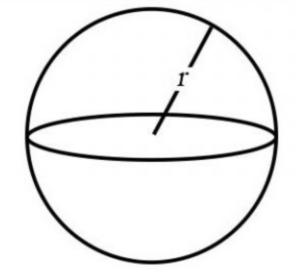
Volume of Sphere:
The volume of a sphere can be found using the formula,
V = (4/3) × π × radius³,
Where “radius” is the distance from the centre of the sphere to its surface.
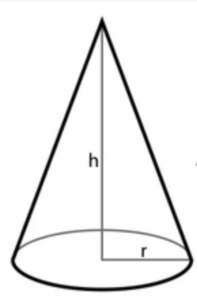
Volume of Cone:
The volume of a cone is given by the formula,
V = (1/3) × π × radius² × height,
Where “radius” represents the radius of the base, and “height” is the perpendicular distance from the base to the tip of the cone.
Volume of Pyramid:
The volume of a pyramid can be calculated using the formula,
V = (1/3) × base area × height,
Where “base area” refers to the area of the base of the pyramid, and “height” is the perpendicular distance from the base to the apex.

It’s important to ensure that the dimensions used in the formulas are consistent (i.e., in the same units) to obtain accurate volume values. Additionally, these formulas provide the volume in cubic units, such as cubic centimetres (cm³) or cubic meters (m³), depending on the units of measurement used for the dimensions.
Understanding these volume formulas is crucial for various applications, such as determining the capacity of containers, calculating the amount of material needed for construction or manufacturing, and solving problems involving three-dimensional shapes and objects.
Solved Examples on Volume Formulae:
Example 1: Finding the volume of a cube
Given: Side length = 5 cm
To find: Volume of the cube
Solution:
The formula for the volume of a cube is: Volume = side³
Substituting the given value, we have:
Volume = 5 cm × 5 cm × 5 cm
Volume = 125 cm³
Therefore, the volume of the cube is 125 cubic centimetres.
Example 2: Finding the volume of a cylinder.
Given: Radius = 3 cm, Height = 10 cm
To find: Volume of the cylinder
Solution:
The formula for the volume of a cylinder is: Volume = π × radius² × height
Substituting the given values, we have:
Volume = 3.14 × (3 cm)² × 10 cm
Volume ≈ 282.6 cm³ (rounded to one decimal place)
Therefore, the volume of the cylinder is approximately 282.6 cubic centimetres.
Example 3: Finding the volume of a sphere
Given: Radius = 4 cm
To find: Volume of the sphere
Solution:
The formula for the volume of a sphere is: Volume = (4/3) × π × radius³
Substituting the given value, we have:
Volume = (4/3) × 3.14 × (4 cm)³
Volume ≈ 268.1 cm³ (rounded to one decimal place)
Therefore, the volume of the sphere is approximately 268.1 cubic centimetres.
Frequently Asked Questions on Volume Formulae:
- What is volume?
Answer: Volume is a measure of the amount of space occupied by a three-dimensional object. It represents the capacity or extent of an object in three dimensions.
- How is volume different from area?
Answer: Volume measures three-dimensional space, whereas area measures two-dimensional space. Area represents the surface of an object, while volume represents the space it occupies.
- What are some common formulas for finding volume?
Answer: The formulas for calculating volume vary depending on the shape of the object. Here are some common volume formulas:
Cube: Volume = side³
Rectangular Prism: Volume = length × width × height
Cylinder: Volume = π × radius² × height
Sphere: Volume = (4/3) × π × radius³
Cone: Volume = (1/3) × π × radius² × height
Pyramid: Volume = (1/3) × base area × height
- Can you find the volume of irregular shapes?
Answer: Yes, the volume of irregular shapes can be determined using different methods. One common approach is to divide the shape into simpler components (such as cubes, cylinders, or prisms), calculate their individual volumes, and then sum them up.
- What units are used to measure volume?
Answer: Volume can be measured using various units, such as cubic centimetres (cm³), cubic meters (m³), cubic inches (in³), or cubic feet (ft³), depending on the scale and context of the problem.
- Can volume have fractions or decimals?
Answer: Yes, the volume can have fractional or decimal values depending on the measurements involved. For example, if you have a cylinder with a radius of 2.5 cm and height of 7.8 cm, the resulting volume can be a decimal value.
- Can you find the volume of a two-dimensional object?
Answer: No, volume is a measure of three-dimensional space. To measure the space occupied by a two-dimensional object, you would use area instead.





