Table of Contents
What is Arc ?
Arc length refers to the distance measured along a curved path or the circumference of a circle. It’s the length of the curved segment, known as the arc. This distance will always be longer than the straight line connecting the two endpoints of the arc, called the chord.
To calculate the length of an arc in a circle with radius r, you use different formulas depending on whether the angle is given in degrees or radians.
- When the angle is in degrees:
The formula for arc length is: Arc Length = 𝑟 × 𝜃 × (𝜋180)
Here, θ is the angle in degrees. The term 𝜋180 converts degrees to radians, which is necessary for the calculation. - When the angle is in radians:
The formula simplifies to: Arc Length = 𝑟 × 𝜃
In this case, θ is already in radians, so no conversion is needed.
What is Arc Length?
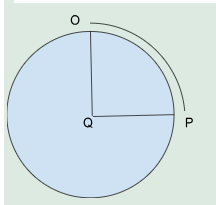
Arc length is the measure of the distance along a curved section of a circle or any curve. It represents the space between two points along this curved path. For a circle, the arc is simply a segment of its circumference.
When discussing arc length, the angle subtended by the arc at the centre of the circle plays an important role. This angle is formed by the two line segments that extend from the circle’s centre to the endpoints of the arc.
For instance, consider a circle where OP is an arc with the centre Q. The length of the arc OP, denoted as L, is the distance you would measure along the curve between the two endpoints of OP.
Arc Length Formula
To derive the formula for arc length, we start by recalling the formula for the circumference of a full circle, which is 2πr, where r is the radius of the circle. The arc is simply a portion of this circumference.
Arc Length in Degrees:
A full circle subtends an angle of 360°. If the angle subtended by the arc is θ, then the arc represents a fraction θ360 of the total circumference.
Therefore, the formula for the arc length L when θ is in degrees is:
Arc Length = θ/360 × 2πr = rθπ180
Arc Length in Radians:
If the angle is given in radians, the calculation becomes simpler. In radians, the angle subtended by the arc is already in the appropriate unit for the formula.
For an angle θ in radians, the formula for arc length L is:
Arc Length=rθ
This is derived from the fact that 1 radian subtends an arc length equal to the radius of the circle.
Types of Arcs
Arcs are segments of a circle’s circumference and can be categorised into different types based on their length and angle. These types are described as follows.
- Minor Arc
A Minor Arc is an arc that measures less than half of the circle’s circumference. The central angle of a Minor Arc is less than 180°. For example, in a given circle, if an arc is subtended by an angle less than 180°, it is considered a Minor Arc. The length of a Minor Arc is calculated using the central angle of the arc which is less than 180°. - Major Arc
A Major Arc spans more than half of the circle’s circumference. The central angle of a Major Arc is more than 180°. In a given circle, if an arc subtends an angle greater than 180°, it is a Major Arc. The measure of a Major Arc can be determined by subtracting the measure of the Minor Arc from 360°. For example, if the Minor Arc is 120°, the Major Arc would be 360° – 120° = 240°. - Semicircle
A Semicircle is an arc that measures exactly 180°. A Semicircle represents exactly half of a circle when it is divided along its diameter. This means it covers the entire half of the circle’s circumference. The length of a Semicircle is half of the circle’s total circumference.
Applications of Arcs
Arcs play a significant role in various fields due to their structural properties.
- Arcs are commonly used in the design of bridges, allowing them to span streams, rivers, and other gaps efficiently.
- Arcs are integral to creating arches over doorways, and windows, and forming domes in buildings, enhancing both functionality and visual appeal.
- Design and Communication.
- Arcs contribute to the aesthetic elements of buildings and structures, improving their visual harmony.
- The design of arcs aids in the efficient transmission of TV and radio signals through high-speed cables.
- The traditional bow used by archers features a prominent arc, which is crucial for its design and performance.
- When an object such as a coin or stone is tossed into the air, it follows a curved arc due to the force of gravity.
Arc Solved Examples
Example: A circle with a radius of 5 units and a central angle of 60° is given. Find the length of the Minor Arc.
Solution: Angle in Radians = pi/3
Use the Arc Length Formula: Arc Length=rθ
where θ is in radians.
Now, Substitute the Values:
Arc Length=rθ = 5 * pi/3 = 5.24
Thus, the length of the Minor Arc is approximately 5.24 units.
Example: A circle with a radius of 8 units and a central angle of 120°. Find the length of the Major Arc.
Solution: Arc Length = θ/360 × 2πr = rθπ/180
where θ=120
Arc Length = θ/360 × 2πr = rθπ/180 = 8 (120) π/180 = 8.38 units
Arc Practice Question
Q. 1. A circle with a radius of 10 units and a central angle of 3 radians. Find the length of the arc.
Q. 2. A circle with a radius of 6 units and an arc length of 15 units. Find the central angle (in radians) subtended by the arc.
Q. 3. A circle with a radius of 4 units and a central angle of 150°. Find the length of the Major Arc.
Q. 4. A circle with a radius of 5 units and a chord length of 6 units. Find the central angle (in radians) subtended by the chord.
Arc FAQs
What is the formula to calculate arc length in radians?
To calculate the arc length when the central angle is in radians, use the formula: Arc Length=θ×r where θ is the central angle in radians and r is the radius of the circle.
How do you find the arc length if the central angle is given in degrees?
When the central angle is in degrees, use the formula: Arc Length = 𝑟 × 𝜃 × (𝜋180) where θ is the central angle in degrees and r is the radius of the circle.
What is the difference between a Major Arc and a Minor Arc?
Minor Arc: An arc that measures less than 180° of the circle’s circumference. It is the shorter of the two arcs connecting the same endpoints. Major Arc: An arc that measures more than 180° of the circle’s circumference. It is the longer arc connecting the same endpoints.
What is the inscribed angle?
The angle subtended by the arc at any point on the circumference of the circle is called an inscribed angle. Find the arc length of a circle that subtends an angle of 120° to the center of a circle whose radius is 24 cm. The length of an arc = 2πr(θ/360) = 2 x 3.14 x 24 x 120/360 = 50.24 cm









